Synopsis

Achieving high spatio-temporal resolutions is challenging in dynamic magnetic resonance imaging (dMRI). It is effective to use low-rank and sparse jointly for dMRI reconstruction. However, the nuclear norm is usually used as a convex approximation of rank function in many low-rank models, so the result is not optimal. In this study, we proposed a novel method used low rank which utilize a nonconvex norm and sparse jointly for dMRI reconstruction. The effectiveness of the proposed method was investigated in phantom and in-vivo experiments.

Introduction

In recent years, low-rank framework has been widely utilized as a powerful tool for image analysis¹, web search², and computer vision³. In dMRI reconstruction, the combination of low rank and sparse achieved good results^{4, 5}. In these methods’ the low-rank representation, the nuclear norm is used as a convex approximation of rank function. However, there had some problems in solving low-rank constraints. In the rank function, the eigenvalue contains the information of the observed data. These methods treated all eigenvalues equally and the algorithm used the same threshold to shrink the eigenvalues, which will cause information loss in reconstructed images. Hence, we proposed the truncated nuclear norm (TNN)⁶ to replace the nuclear norm to recover more information from the observed data in the low-rank and sparse prior based reconstruction method. The proposed method was tested in phantom and in-vivo experiments.

Method

Theory: When the matrix has a low-rank structure, the noise should be contained in relatively small eigenvalues, so the error of the noise depends on the sum of the small eigenvalues. Given a matrix $$$X,Y\in\mathbb{C}^{m\times n},\tau>0,l=min(m,n)$$$,the rank’s truncated parameter $$$t$$$, the noise information is largely determined by the number of non-zero elements of the minimum $$$l-t$$$ eigenvalues. The TNN is defined as follows:$$‖X‖_{t,*}=‖σ(X)‖_{t,*}=∑_{i=t+1}^l‖σ_i (X) ‖=∑_{i=1}^{l}‖σ_i (X) ‖-∑_{i=1}^t‖σ_i (X) ‖\quad(1)$$So we propose the truncated nuclear norm minimization model combined with sparse prior:$$\underset{L,S}{min}‖L‖_{t,*}⁡+\mu‖TS‖_1\quad s.t.E(L+S)=d\quad(2)$$where $$$T$$$ is a sparsifying transform for $$$S$$$, $$$E$$$ is the encoding or acquisition operator. $$$L$$$ and $$$S$$$ are defined as space-time matrices, where each column is a temporal frame and $$$d$$$ is the under-sampled $$$k-t$$$ data. A version of Eq. (2) using regularization rather than strict constraints can be formulated as follows:$$\underset{L,S}{min}\frac{1}{2}‖E(L+S)-d‖_2^2⁡+\lambda‖L‖_{t,*}+\mu‖TS‖_1\quad (3)$$where the parameters $$$\lambda$$$ and $$$\mu$$$ are used to trade off data consistency. We solve the optimization problem in Eq. (3) using iterative soft-thresholding of the singular values of $$$L$$$ and of the entries of $$$TS$$$. Some TNN related method proposed the exact solution with von Neumann’s lemma^{7, 8}. So the optimal solution of $$$L$$$ can be expressed by the TNN operator defined as:$$\mathbb{T}_{t,τ} (L)=U_L (D_{L_1}+S_\tau [D_{L_2}]) V_L^H=L_1+U_{L_2} S_\tau[D_{L_2} ] V_{L_2}^H\quad (4)$$where$$$D_{L_1}=diag(\sigma_1^L,...,\sigma_t^L,0,...,0)$$$,$$$D_{L_2}=diag(0,...,0,\sigma_{t+1}^L,...,\sigma_t^L)$$$and$$$S_\tau[\circ]=sign(\circ)\cdot max(|\circ|-\tau)(\tau=\frac{\lambda}{\beta})$$$is the soft-thresholding operator. And the optimal solution of $$$TS$$$ can be expressed by the soft-thresholding. The whole process is shown in Algorithm.1.
Phantom and in-vivo experiments: The datasets include the PINCAT numerical phantom data^{9, 10}, in vivo cardiac perfusion MRI data⁴ and the actual scan of cardiac cine data. The scan of cardiac cine data was performed on a 3T MR scanner (Ingenia CX, Philips Healthcare, Best, Netherlands).The datasets are all fully sampled, and simulated trajectories and under-sampling processing are carried out.
Image reconstruction was performed in MATLAB compare with some popular methods including k-t SLR⁴, k-t SPARSE SENSE¹¹ and L+S method⁵.
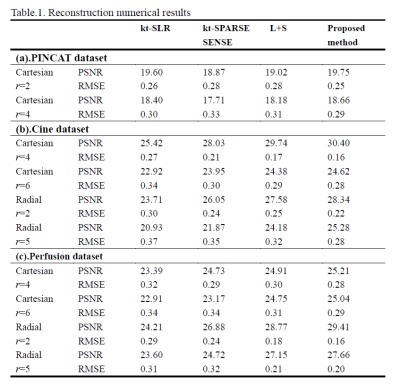
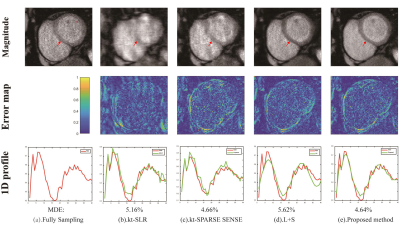
Reconstruction performance was evaluated using the PSNR and RMSE. In the perfusion dataset, in order to calculate the signal intensity , we defined the MDE. In specifically, we choose ten points in the blood pool and myocaridal regions randomly. Then we calculated the distance between the original signal and the reconstructed signal at each frame, and averaged all the points.

Results

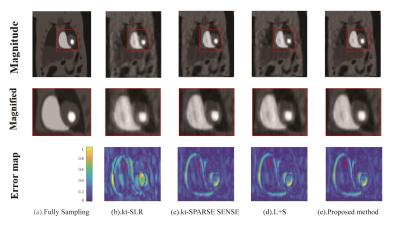
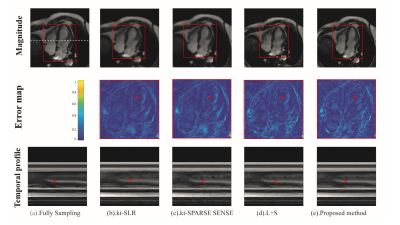
In PINCAT dataset, for reconstruction of the heart, the proposed method had low artifacts with Cartesian trajectory and r=2 as shown in FIG.1. In the cardiac cine dataset, the proposed method also had good reconstruction results of cardiac blood pools with radial trajectory and r=2 as shown in FIG.2. We also took more attention to changes in myocardial contractility. As shown in FIG.2 by the arrows in the temporal profile, the methods to be compared present temporal blurring artifacts, which are effectively removed by the proposed mothed. And the proposed mothed presents higher temporal fidelity than the other methods. In perfusion dataset, the proposed method had clear reconstruction results of myocardial boundaries with Cartesian trajectory and r=4 as shown in FIG.3. From the 1D profile in FIG.3, we can clearly see that the proposed method is closer to the original signal strength value than the other methods.
The proposed method also had better numerical reconstruction results compare with other methods in three datasets as shown in Table.1.
All experiments clearly illustrate that the proposed method can get better reconstruction results than other methods in terms of both robustness and effectiveness.

Discussion and Conclusions

A novel low-rank modeling and sparsity constrained reconstruction method was introduced for dMRI. The proposed model has an improved approximation effect for low-rank prior. The proposed method has stronger robustness, and its effectiveness has been demonstrated with phantom and in vivo experiments. Although not addressed here, the proposed method may also be applicable to other low-rank based method. And its utility should be fully explored in future studies

Acknowledgements

None