1175

Low-rank and Framelet Based Sparsity Decomposition for Reconstruction of Interventional MRI in Real Time

Zhao He¹, Ya-Nan Zhu², Suhao Qiu¹, Xiaoqun Zhang², and Yuan Feng¹
¹Institute for Medical Imaging Technology, School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, ²School of Mathematical Sciences, MOE-LSC and Institute of Natural Sciences, Shanghai Jiao Tong University, Shanghai, China

Synopsis

A low-rank and sparsity (LS) decomposition algorithm with framelet transform was proposed for real-time interventional MRI (i-MRI). Different from the existing LS decomposition, we exploited the spatial sparsity of both the low-rank and sparsity components. A primal dual fixed point (PDFP) method was adopted for optimization to avoid solving subproblems. We carried out intervention experiments with gelatin and brain phantoms to validate the algorithm. Reconstruction results showed that the proposed method can achieve an acceleration of 40 folds.

Introduction

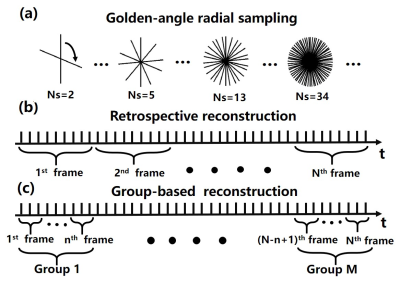
Fast data acquisition and image reconstruction are necessary for interventional MRI (i-MRI) to guide interventional surgery in real-time ^1,2. Reconstruction of undersampled data using partially separable (PS) function for low-rank constraint, has been successfully applied in dynamic MRI ^3-5, and combined with compressed sensing (CS) ^6,7. Low-rank together with sparsity has also been used in the reconstruction of dynamic MR images ^8-10. However, the retrospective reconstruction scheme for dynamic images may not apply to i-MRI, especially in real-time scenarios. In this study, using a golden-angle radial sampling and a group-based reconstruction scheme, we proposed a low-rank and sparsity decomposition (LS) with framelet transform (LSF) for the reconstruction of i-MRI. The spatial sparsity constraints of the low-rank and sparsity components were utilized. A primal dual fixed point (PDFP) algorithm was adopted for optimization. Simulation and phantom interventional experiments were implemented for validation.

Methods

In i-MRI, the background and the interventional feature could be separated into a low-rank matrix $$$ \bf L $$$ and sparse matrix $$$ \bf S $$$. The LS decomposition with framelet transform (LSF) is:
$$ \left\{\bf L,\bf S\right\}= \arg\min_ { \bf L, \bf S} \frac{\tt 1}{\tt 2}\lVert \bf E(\bf L + \bf S) - \bf d \tt\rVert_2^2 + \tt \lambda_L \lVert \bf L \tt\rVert_* + \lambda_S \lVert \nabla_t \bf S \tt \rVert_1 + \tt \tt\lambda_L^{\psi} \lVert \psi \bf L \tt\rVert_1 + \tt\lambda_S^{\psi} \lVert \psi \bf S \tt\rVert_1, $$
where $$$ \bf E $$$ is the encoding function, $$$ \bf d $$$ is the acquired k-space data, $$$ \nabla_t $$$ represents a total-variation along the temporal direction of $$$ \bf S $$$, $$$ \psi $$$ is the framelet transform, $$$ \tt\lambda_L \ $$$, $$$ \tt\lambda_S \ $$$, $$$ \tt\lambda_L^{\psi} \ $$$ and $$$ \tt\lambda_S^{\psi} \ $$$ are the regularization parameters. To avoid solving the complex subproblems that lack a general termination criterium, we proposed to use a primal dual fixed point (PDFP) algorithm ¹¹ rather than the commonly used alternating direction of multipliers (ADMM) ⁹ or singular value thresholding (SVT) ¹⁰. The PDFP for the LSF model was abbreviated as LSFP.

To satisfy the real-time requirement in i-MRI, we adopted a golden-angle radial sampling combined with a group-based reconstruction scheme (Figure 1). K-space data was continuously acquired during the intervention process. In this study, only 10 radial spokes were used for reconstructing one frame, and we took 5 frames for each reconstruction group. Therefore, only 50 radial spokes were needed for a reconstruction of one group. This is equivalent to an acceleration factor of 40.

To evaluate the proposed reconstruction method, 200 brain intervention images were generated from a reference brain MR image ¹². The nonuniform fast Fourier transform (NUFFT) was applied to simulate the radial sampling. The k-space data was acquired with 512 readout points, a total of 2000 radial spokes, and 8 channels. Two interventional experiments were also carried out with a homogeneous gelatin phantom and a porcine brain using a 3T MRI scanner (uMR 790, United Imaging Healthcare, Shanghai, China). For both phantoms, a total of 2000 golden-angle radial spokes sampling 512 points in readout direction with 24 channels were acquired during the intervention. The reconstruction results from LSFP were compared with those from Golden-angle RAdial Sparse Parallel MRI (GRASP) ¹³.

Results

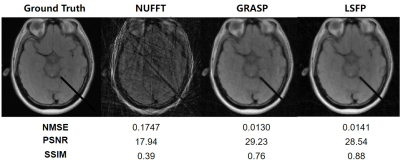
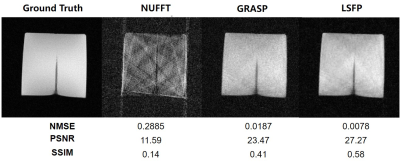
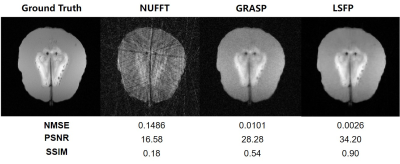
Reconstruction of the simulated interventional images shows that LSFP performed better than NUFFT and GRASP methods (Figure 2). A set of interventional MR images of the gelatin phantom were reconstructed by NUFFT, GRASP, and LSFP (Figure 3). LSFP yielded the least artifacts, and the NMSE, PSNR, and SSIM for LSFP method were 0.0078, 27.27, and 0.58, respectively. This demonstrates the robustness of the proposed method. Compared with other methods, LSFP generated the least artifacts in the i-MRI of the brain phantom (Figure 4). In terms of NMSE, PSNR, and SSIM, LSFP also had the best performance.

Conclusion

In this study, we proposed a new method for accelerating i-MRI by combining the improved LS decomposition algorithm with golden-angle radial sampling and group-based reconstruction methods. The proposed method takes advantage of the spatial sparsity of the low-rank and sparsity components using framelet transform for fast i-MRI reconstruction. To avoid subproblems, a PDFP algorithm was used for optimization. Gelatin and brain phantom experiments showed the robustness of the proposed method. The improved temporal resolution demonstrates the potential of the proposed method for real-time i-MRI.

Acknowledgements

Funding support from grant 31870941 from National Natural Science Foundation of China (NSFC) and grant 1944190700 from Shanghai Science and Technology Committee (STCSM) are acknowledged. We thank Prof. Zhi-Pei Liang from UIUC for helpful discussions.

References

1. Zufiria B, Qiu S, Yan K, Zhao R, Wang R, She H, Zhang C, Sun B, Herman P, Du Y, Feng Y. A feature-based convolutional neural network for reconstruction of interventional MRI. NMR Biomed 2019.

2. Campbell-Washburn AE, Faranesh AZ, Lederman RJ, Hansen MS. Magnetic Resonance Sequences and Rapid Acquisition for MR-Guided Interventions. Magn Reson Imaging Clin N Am 2015;23(4):669-679.

3. Liang Z-P, Ieee. Spatiotemporal imaging with partially separable functions. 2007 4th Ieee International Symposium on Biomedical Imaging : Macro to Nano, Vols 1-3, IEEE International Symposium on Biomedical Imaging; 2007. p 988-991.

4. Lam F, Liang Z-P. A Subspace Approach to High-Resolution Spectroscopic Imaging. Magn Reson Med 2014;71(4):1349-1357.

5. Nakarmi U, Wang Y, Lyu J, Liang D, Ying L. A Kernel-Based Low-Rank (KLR) Model for Low-Dimensional Manifold Recovery in Highly Accelerated Dynamic MRI. IEEE Trans Med Imaging 2017;36(11):2297-2307.

6. Fu M, Zhao B, Carignan C, Shosted RK, Perry JL, Kuehn DP, Liang Z-P, Sutton BP. High-Resolution Dynamic Speech Imaging with Joint Low-Rank and Sparsity Constraints. Magn Reson Med 2015;73(5):1820-1832.

7. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang Z-P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn Reson Med 2015;74(2):489-498.

8. Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated Dynamic MRI Exploiting Sparsity and Low-Rank Structure: k-t SLR. IEEE Trans Med Imaging 2011;30(5):1042-1054.

9. Tremoulheac B, Dikaios N, Atkinson D, Arridge SR. Dynamic MR Image Reconstruction-Separation From Undersampled (k, t)-Space via Low-Rank Plus Sparse Prior. IEEE Trans Med Imaging 2014;33(8):1689-1701.

10. Otazo R, Candes E, Sodickson DK. Low-Rank Plus Sparse Matrix Decomposition for Accelerated Dynamic MRI with Separation of Background and Dynamic Components. Magn Reson Med 2015;73(3):1125-1136.

11. Chen P, Huang J, Zhang X. A primal-dual fixed point algorithm for convex separable minimization with applications to image restoration. Inverse Problems 2013;29(2).

12. Ji JX, Son JB, Rane SD. PULSAR: A MATLAB toolbox for parallel magnetic resonance imaging using array coils and multiple channel receivers. Concepts Magn Reson Part B 2007;31B(1):24-36.

13. Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, Axel L, Sodickson DK, Otazo R. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med 2014;72(3):707-717.

Figures

Figure 1. Illustrations of the data acquisition and reconstruction scheme. (a) A continuous golden-angle radial sampling method was used for i-MRI in this study (golden angle = 111.25^°). (b) Conventional dynamic image reconstruction based on a retrospective scheme. (c) The proposed group-based reconstruction method for real-time i-MRI reconstruction.

Figure 2. A comparison of different algorithms. The ground truth is the 150th simulated brain intervention image. A group-based reconstruction strategy (10 spokes per frame, 5 frames per group, a total of 200 frames for 2000 spokes) was adopted for reconstruction using NUFFT, GRASP, and LSFP. The acceleration factor was about 40.

Figure 3. A comparison of reconstructed interventional images of gelatin. The ground truth was retrospectively reconstructed with the LS algorithm (50 spokes per frame, total 40 frames for 2000 spokes). A group-based reconstruction strategy (10 spokes per frame, 5 frames per group, a total of 200 frames for 2000 spokes) was adopted for reconstruction using NUFFT, GRASP, and LSFP. The acceleration factor was about 40.

Figure 4. A comparison of reconstructed interventional images of brain phantom. The ground truth was retrospectively reconstructed with the LS decomposition (50 spokes per frame, a total of 40 frames for 2000 spokes). A group-based reconstruction strategy was also adopted for NUFFT, GRASP, and LSFP algorithms (10 spokes per frame, 5 frames per group, total 200 frames for 2000 spokes). The acceleration factor was about 40.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1175