1171
Highly undersampled GROG-BPE radial data reconstruction using Compressed Sensing
Yumna Bilal1,2, Ibtisam Aslam1,3, Muhammad Faisal Siddiqui1, and Hammad Omer1
1Medical Image Processing Research Group (MIPRG), Department of Electrical & Computer Engineering, COMSATS University Islamabad, Islamabad, Pakistan, 2Department of Electrical Engineering, University of Gujrat, Gujrat, Pakistan, 3Service of Radiology, Geneva University Hospitals and Faculty of Medicine, University of Geneva, Geneva, Switzerland
1Medical Image Processing Research Group (MIPRG), Department of Electrical & Computer Engineering, COMSATS University Islamabad, Islamabad, Pakistan, 2Department of Electrical Engineering, University of Gujrat, Gujrat, Pakistan, 3Service of Radiology, Geneva University Hospitals and Faculty of Medicine, University of Geneva, Geneva, Switzerland
Synopsis
This work aims at reconstructing the undersampled non-Cartesian k-space signals by generating a cloud of randomly located additional points through GRAPPA Operator Gridding (GROG) facilitated Bunch Phase Encoding (BPE) collectively termed as GROG-BPE scheme. Gridding of this data is performed onto a Cartesian grid. Inherent randomness in the gridded BPE data is exploited using Compressed Sensing (CS) to obtain the solution image at higher acceleration factors and the results are compared with conventional CG-INNG method. Every step in the proposed method (right from BPE generation to reconstruction) is self-calibrating and does not require additional calibration signals.
Introduction
Bunch Phase Encoding (BPE) scheme, based on Papoulis’s generalized theorem of undersampling, has been presented in the past to reduce the scan time by adding a bunch of additional k-space samples acquired around every source point1. Instead of acquiring these additional points through specialized pulse sequence, Seiberlich2 proposed Self-Calibrating GRAPPA Operator Gridding (SC-GROG)3 to calculate these additional points offline for radial MRI data. However, the reconstruction of GROG mimicked BPE (termed as GROG-BPE) through previously proposed Conjugate Gradient Iterative Next Neighborhood (CG-INNG)4 algorithm has been confined to lower acceleration factors (AF). This work proposes a Compressed Sensing (CS) reconstruction of the GROG-BPE data (CS-GROG-BPE) for highly undersampled radial acquisitions to achieve better results. The proposed CS-GROG-BPE results are compared with the previously proposed GROG-BPE CG-INNG2 technique.Methods
Figure 1 shows a schematic illustration for the proposed CS-GROG-BPE approach. Undersampled non-Cartesian k-space and its trajectory is used to generate the randomly blipped BPE signals using GROG. The weight sets required are computed from the undersampled data itself and no additional calibration data is required3. Values of two important generation parameters i.e. number of bunch points (NBP) and maximum distance of a calculated bunch point from its source point (k_max) have been worked out for a range of possibilities and the optimal values of 81 and 0.3 have been chosen for both the parameters respectively.Generated BPE signal is then distributed to a Cartesian grid using SC-GROG3. If compressed sensing reconstruction is performed right after BPE signal generation, the iterative algorithm has to de-grid and grid data, back and forth between Cartesian and non-Cartesian trajectory in order to evaluate data consistency in each iteration5. This repetitive de-gridding and gridding is not only computationally extensive (considering an overly large BPE data due to additional bunch points), but even more cumbersome for a non-standardized trajectory like BPE. A quick fix to this problem, inspired from6,7 is to grid the BPE data to Cartesian before compressed sensing, using SC-GROG. Unlike other commonly used gridding techniques, SC-GROG leaves some empty spaces in the Cartesian gridded data5 that results into a sparsely sampled k-space, favorable for CS reconstruction8.
Underlying algorithm behind compressed sensing reconstruction used in this paper is Non-linear Conjugate Gradient (NLCG). Both the wavelet transform and total variation(TV) have been used as transform operators. Regularization parameters for both the operators have been tuned for optimal results using grid search. Multi-channel BPE data is processed one after the other, with individual coil method (ICM)9 and then combined with sum-of-square reconstruction. Hence the proposed method does not require knowledge of receiver coil sensitivity profiles at any step.
Results of CS-GROG-BPE (proposed method) and GROG-BPE CG-INNG on the radial data with the same parameters are compared on the basis of Artifact Power (AP), Signal-to-Noise Ratio (SNR) and Root Mean Square Error (RMSE)10.
Results and Discussion
The proposed CS-GROG-BPE is tested on human head MRI data obtained using 1.5T GE scanner with dimensions $$$(256 × 256 × 8)$$$, where $$$256 × 256$$$ is the matrix size and 8 multi-channel head-coils. The other parameters were: TE/TR = 10/500 ms, FOV = 20 cm, slice thickness = 3 mm and flip angle = 50º. Initially, the human head data was acquired in Cartesian sampling and then de-gridded to radial trajectory with 256 read points and 402 projections with a base matrix of 2562, using Fessler toolbox11. Fully sampled radial data is then retrospectively undersampled at AF= 8, 10 and 12, with 51, 41 and 34 radial spokes, respectively.Figure 2 shows the reconstruction results of the proposed CS-GROG-BPE and GROG-BPE CG-INNG scheme. Figure 2(a) shows the fully sampled Cartesian image taken as a reference. Figure 2(b) depicts the reconstruction results of the proposed method at accelerations factors of 8, 10 and 12 (from left to right). Figure 2(c) shows the reconstruction results of GROG-BPE CG-INNG2 with the same acquisition protocol i.e. undersampling, BPE generation and gridding parameters. Quantifying parameters in terms of AP, RMSE and SNR have been given under each of the reconstructed images in Figure 2(b-c).
It can be observed that the results obtained from the proposed CS-GROG-BPE method given in Figure 2(b) are better in terms of image clarity, showing less artifacts as compared to GROG-BPE CG-INNG reconstructions in Figure 2(c). The quantifying parameters of CS-GROG-BPE reconstructed images show a significant percentage improvement e.g. 37.9%, 21.4% and 30.5% in AP, RMSE and SNR respectively, over the images reconstructed by GROG-BPE CG-INNG at an acceleration factor of 8.
Conclusion
This work outlines Compressed Sensing(CS) reconstruction for radially undersampled GROG-BPE data. Reconstruction results illustrate how the proposed CS-GROG-BPE method outperforms the previously proposed GROG-BPE CG-INNG2 at higher acceleration factors, in terms of better image quality and superior quantifying parameters. There is a percentage improvement of 46.0%, 26.4% and 16.8% in AP, RMSE and SNR respectively at an acceleration factor of 10.Acknowledgements
No acknowledgementReferences
- Moriguchi, H. & Duerk, J. L. Bunched phase encoding (BPE): a new fast data acquisition method in MRI. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 55, 633-648 (2006).
- Seiberlich, N. et al. Using the GRAPPA operator and the generalized sampling theorem to reconstruct undersampled non‐Cartesian data: Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 61, 705-715 (2009).
- Seiberlich, N., Breuer, F., Blaimer, M., Jakob, P. & Griswold, M. Self‐calibrating GRAPPA operator gridding for radial and spiral trajectories. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 59, 930-935 (2008).
- Moriguchi, H. & Duerk, J. L. Iterative Next‐Neighbor Regridding (INNG): Improved reconstruction from nonuniformly sampled k‐space data using rescaled matrices. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 51, 343-352 (2004).
- Seiberlich, N. et al. Non‐Cartesian data reconstruction using GRAPPA operator gridding (GROG). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 58, 1257-1265 (2007).
- Shahzadi, I., Aslam, I., Qazi, S. A. & Omer, H. Golden-Angle Radial Sparse Parallel MR Image Reconstruction Using SC-GROG Followed by Iterative Soft Thresholding. Applied Magnetic Resonance 50, 977-988 (2019).
- Aslam, I., Najeeb, F. & Omer, H. Accelerating MRI using GROG gridding followed by ESPIRiT for non-Cartesian trajectories. Applied Magnetic Resonance 49, 107-124 (2018).
- Lustig, M., Donoho, D. & Pauly, J. M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 58, 1182-1195 (2007).
- Qureshi, M., Junaid, M., Najam, A., Bashir, D., Ullah, I., Kaleem, M., & Omer, H. Image reconstruction using compressed sensing for individual and collective coil methods: Biomedical Research 2016; Special Issue: S287-S292.
- Chow, L. S., Rajagopal, H., Paramesran, R. & Initiative, A. s. D. N. Correlation between subjective and objective assessment of magnetic resonance (MR) images: Magnetic resonance imaging 34, 820-831 (2016).
- Fessler, J. A. Michigan Image Reconstruction Toolbox (MIRT), available at https://web.eecs.umich.edu/~fessler/code/index.html downloaded 30 June 2020.
Figures

Figure 1:
Block diagram of the proposed CS-GROG-BPE scheme. Undersampled radial signal is
used to generate the Bunch Phase Encoded k-space at the specified k_max and
NBP, using GROG. Non-Cartesian BPE k-space is gridded to Cartesian k-space
using a defined oversampling factor and step-size using GROG. Gridded k-space
is then reconstructed coil-by-coil by CS algorithm with specified
regularization parameters. Coil-by-coil reconstructed images are then combined
using sum-of-square reconstruction to yield the final output image.
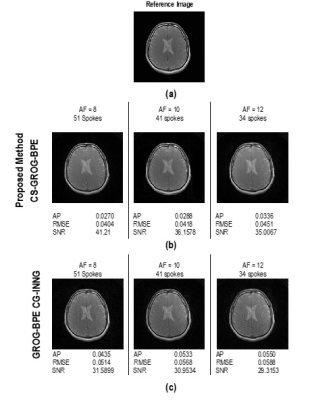
Figure 2: Reconstruction Results (a) shows fully sampled
ground truth image. (b) shows results of CS-GROG-BPE method proposed in this
work, at acceleration at AF = 8, 10, 12. (c) shows results of GROG-BPE CG-INNG method2
with the same BPE generation and gridding parameters. Quantifying parameters
including AF, RMSE and SNR have been provided underneath each reconstructed
image.