INTRODUCTION

The blipped-CAIPIRINHA simultaneous multi-slice (SMS) scheme¹ and corresponding split slice-GRAPPA (SG) reconstruction² have been widely used to substantially reduce scan time in echo-planar imaging (EPI) studies without compromising image quality. Different to the other SMS application with single-kernel SG reconstruction, a dual-kernel SG (SG-DK) has been introduced as a robust method to improve the inter-slice ghosting artifact specific to SMS EPI, in which separated SG kernels are created for odd and even k-space lines³. The g-factor in the parallel imaging describes the spatially variant noise enhancement, which is essential for reconstruction assessment and can be further used as supplementary information for SNR improvement⁴. A standard way for analytical g-factor calculation of Cartesian GRAPPA reconstruction has been proposed⁵. In essence, the convolution operation in k-space is formulated as a multiplication in the image domain, where SENSE-like noise propagation analysis can be performed. This concept has been extended to be compatible with SG-DK reconstruction^6-7. It computes the sum of odd-even kernels in image domain for an averaged ghost correction and the difference for slice-specific residual ghost correction, then combine the two to mimic the ghost reduction in SG-DK. Here, we develop a more accurate prescription to calculate the g-factor in SG-DK reconstruction. The approach was validated in a phantom study.

METHODS

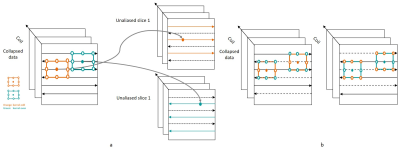
The key to accurately formulate SG-DK reconstruction in image space is to consider even and odd source lines separately. Accordingly, the GRAPPA kernel coefficients, which are originally arranged by output line (even/odd) are rearranged according to source line (even/odd). Image reconstruction then amounts to the sum of individual reconstructions of – now consistent – partial reconstructions of even and odd sets.
Fig.1 shows the kernel rearranging method, where (a) shows the SG-DK method to obtain the k-space data for a unaliased slice and (b) shows the rearranged kernels applied on odd and even lines of the collapsed slice, respectively.
Based on the standard analytical g-factor calculation method⁵, we first transform the SG-DK reconstruction to a voxel-wise multiplication in image space by using the new rearranged kernels. Assuming N receiver coils, the k^th channel of reconstructed unaliased image $$$I_k^{unaliased}$$$ in image domain will be:
$$I_k^{unaliased}(x,y) = \sum_{l=1}^NW_{odd}\cdot I_l^{collapsed}(x,y_{odd}) + \sum_{l=1}^NW_{even}\cdot I_l^{collapsed}(x,y_{even}) \hspace{1cm}[1]$$
where $$$I_l^{collapsed}(x,y_{odd})$$$ and $$$I_l^{collapsed}(x,y_{even})$$$ are the inverse Fourier-transformed images of $$$l^{th}$$$ channel from the zero-padded two k-space sets, which include odd and even lines from collapsed data, respectively; $$$W_{odd}$$$ and $$$W_{even}$$$ are rearranged SG kernel weights in image domain.
The corresponding g-factors $$$g_{comb,odd}$$$ and $$$g_{comb,even}$$$ for coil combined images can be given by:
$$g_{comb,odd} = \frac{\sqrt{\mid p^T\cdot(W_{odd}\Psi)\cdot\Sigma^2\cdot(p^T\cdot(W_{odd}\Psi))^H\mid}}{\mid (p^T\cdot1)\cdot\Sigma^2\cdot(p^T\cdot1)^H\mid};g_{comb,even} = \frac{\sqrt{\mid p^T\cdot(W_{even}\Psi)\cdot\Sigma^2\cdot(p^T\cdot(W_{even}\Psi))^H\mid}}{\mid (p^T\cdot1)\cdot\Sigma^2\cdot(p^T\cdot1)^H\mid} \hspace{1cm}[2]$$
where p is the vector for channel combination coefficients; $$$\Sigma$$$ is the noise correlation matrix; $$$\Psi$$$ is any in-plane GRAPPA kernel in image domain, if performed in combination with the SG reconstruction. It is advantageous to remove the noise correlation matrix from the equation [2] by performing a noise decorrelation prior to image reconstruction⁸.
Given an un-correlated noise distribution in disjunct sets of k-space data, the compound g-factor g_eff can be found as the voxel-wise square root of the average of the squared g-factor values applied on both parts of k-space:
$$g_{eff}=\sqrt{\frac{g_{comb,odd}^2 +g_{comb,even}^2 }{2}} \hspace{1cm}[3]$$
In addition, because the phase correction for N/2 ghosts was done after SG-DK reconstruction, but before the in-plane GRAPPA reconstruction, it will disturb the noise distribution and lead to an imprecise g-factor estimation if not considered. This was done by performing the same phase correction before the combination with the in-plane GRAPPA kernel.
To demonstrate and validate the accuracy of the proposed g-factor calculation prescription, the pseudo multiple-replica SNR measurement method⁹ was used as a reference. In addition, we propose an efficient and intuitive check: as in the pseudo multiple-replica method, we generate synthetic noise of the same characteristics as the real noise, but perform the reconstruction procedures only on it once, then divide the reconstructed noise by the calculated noise map. The resulting noise image should be flat and have a unit RMS value.
All measurements were performed on a commercial 1.5T scanner (MAGNETOM Aera, Siemens Healthcare, Erlangen, Germany) equipped with a 20-channel head/neck coil. Diffusion-weighted images were acquired using SMS EPI with SG-DK reconstruction, as well as in-plane GRAPPA (TE/TR = 74/2800ms, matrix size = 176x176, SMS factor = 2, in-plane GRAPPA factor = 2, FOV shift = 4). All image reconstruction and g-factor calculations were performed inline.

RESULTS

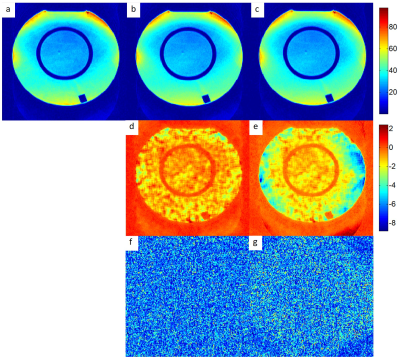
Fig.2a-c shows the quantitative SNR maps from the pseudo multiple-replica method, and our proposed method with and without kernel phase correction, respectively. There is excellent agreement between SNR maps calculated with the pseudo multiple-replica method and the analytical method (Fig.2d, 2f). Note that noise map error due to the missing phase correction from Fig. 2c/e/g is considerable.

DISCUSSION

We developed a novel g-factor calculation method for SG-DK by rearranging measured data and kernel coefficients that apply to odd and even EPI lines respectively. To account for the effect of EPI phase correction, the SG kernels are phase corrected before the combination with the in-plane GRAPPA kernel.

CONCLUSION

The proposed g-factor calculation method allows a practical, accurate quantification of the noise map in SG-DK reconstructions. We demonstrated its consistency with the reference standard.

Acknowledgements

The authors thank Dr. Congyu Liao for helpful discussions.