Introduction

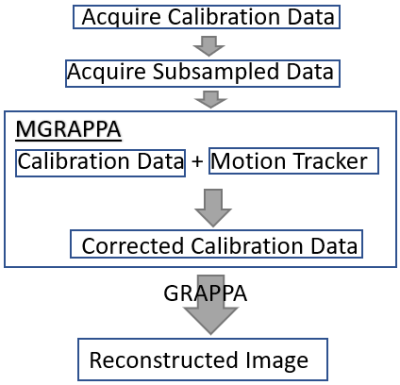
Subject motion is inevitable in MRI. Motion artifacts can be partially corrected using post-processing or prospective correction methods [3]. Here, we consider motion-induced image reconstruction errors for parallel imaging (PI). Calibration data are often acquired in the beginning of the entire imaging process. When motion occurs later, the pre-motion calibration data no longer match the spatial position and the corresponding coil sensitivity encoding of the subsampled data. The purpose of this study is to update reconstruction coefficients, with a focus on k-space based PI reconstruction using the Generalized Autocalibrating Partially Parallel Acquisition (GRAPPA) algorithm [1,2]. A similar concept has been extended to the image-based reconstructions using the Sensitivity Encoding (SENSE) method [4,5].

With prospective motion correction (PMC), raw data are properly aligned in k-space, but subsequent GRAPPA reconstructions can show image artifacts since RF coils are stationary relative to the moving object. The problem can be solved by reacquiring GRAPPA kernels and re-scanning calibration data, but this is commonly impractical and requires additional scan time. Our new method, which we call MGRAPPA, recalculates GRAPPA kernels using motion tracking data to create a more stable and accurate reconstruction.

Theory

Figure 1 shows a flowchart of MGRAPPA in a typical PI scan. For each RF coil, a fully sampled calibration data set (centered in k-space) and an under-sampled data set are acquired. GRAPPA recovers missing k-space data by convolving the sub-sampled data with kernels calculated from calibration data. For MGRAPPA, the acquisitions remain unchanged, but the GRAPPA kernels are updated by reconstructing low-resolution coil sensitivity maps from the calibration data, transforming sensitivity maps inversely to subject motion, and recalculating calibration data and finally GRAPPA kernels.

From each coil, we get $$$P_i^{0,0,0}f$$$ in the form of a matrix. First, we approximate the low frequencies of the signal, $$$f$$$, (ex: brain) by
$$L(f(x,y)) \approx \tilde f^l(x,y):=\sum_{i=1}^n | L(P_i^{0,0,0} f(x,y))|.$$
The approximation $$$\tilde f^l(x,y)$$$ is reasonable because the coil profiles, $$$P$$$, (superscripts are rotation, $$$\theta$$$, and translation, $$$x,y$$$, of coil profile and subscript is coil profile index) are approximately a partition of unity and lowpass, denoted $$$L$$$ ($$$L$$$ clears high frequency coefficients of the FFT), is linear. Set $$$\epsilon>0$$$ small and then approximate $$$P_i^{0,0,0}$$$ by
$$P_i^{0,0,0}(x,y) \approx \tilde P_i^{0,0,0}(x,y):=L(P_i^{0,0,0} f(x,y))/(\tilde f^l(x,y)+\epsilon \max_{x,y} | \tilde f^l(x,y)|).$$
The approximation $$$\tilde P_i^{0,0,0}(x,y)$$$ is reasonable because the profiles are very smooth. Then this implies that the high frequencies of $$$f$$$ in the numerator get removed by $$$L$$$ and then the low frequencies of $$$f$$$ in the numerator get removed by division with approximate low frequencies of $$$f$$$ denoted $$$\tilde f^l$$$ where $$$\epsilon$$$ is added to avoid division by 0 and increase robustness. Then
$$P_i^{\theta,x_0,y_0}(x,y)\approx\tilde P_i^{\theta,x_0,y_0}(x,y)=\tilde P_i^{0,0,0}(R_\theta(x,y)+(x_0,y_0)).$$
So now we have the matrices $$$\tilde f^l$$$ and $$$\tilde P_i^{\theta,x_0,y_0}$$$. Take the product and use the approximation $$$P_i^{\theta,x_0,y_0} f \approx \tilde P_i^{\theta,x_0,y_0} \tilde f^l $$$. The frequencies in the calibration region of this approximation is used to compute the new GRAPPA kernel and then reconstruct the subsampled image, see algorithm/pseudocode in Figure 2.

Simulation Method

Simulation k-space data was synthesized based on coil sensitivity maps calculated from a phantom experiment and clinical 3-D MP-RAGE coil-combined brain images previously acquired. The phantom experiment was conducted on a 3T Prisma scanner (Siemens,Erlangen,Germany) using a 20-channel head coil and a spherical water phantom (3-D MP-RAGE; FOV = 240×240$$$mm^2$$$, resolution = 0.9×0.9×0.9$$$mm^3$$$, 256×256×256, 256 slices, TR/TE/TI = 2600/2.29/1350ms, flip angle $$$8^{\circ}$$$). The human MP-RAGE brain images were acquired on a 3T TrioTim scanner (Siemens) (FOV 256×256$$$mm^2$$$, resolution 1×1×1$$$mm^3$$$, 256×256×160, 160 slices, TR/TE/TI = 2600/4.47/1000ms, flip angle $$$12^{\circ}$$$).

In Vivo Experiment

Brain MRI was performed in a healthy volunteer (after obtaining consent) who was trained to rotate the head by $$$7^{\circ}$$$ to the left upon instruction in the middle of the scan. This experiment was conducted on a 3T Prisma with a 20-channel head coil and MP-RAGE sequence with FOV 240×240$$$mm^2$$$, resolution 1.9×1.9×1$$$mm^3$$$, 128×128×224, 224 slices, TR/TE/TI=2300/2.29/900ms, flip angle $$$8^{\circ}$$$.

Simulation Results

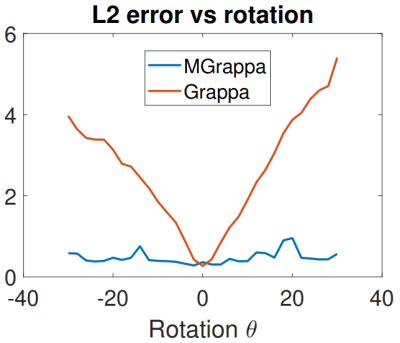
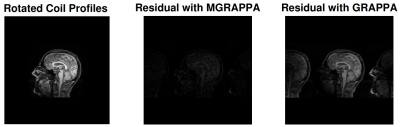
When rotation occurs with PMC, the apparent effect is inverse rotation of coil profiles by the same amount. In this experiment, we use a brain scan as the signal, and we use scans of a disk as profiles. Simulation parameters were: 20 coils, full resolution 256x256, calibration data 24*2 lines and $$$\epsilon=.05$$$. We simulate rotation of the profiles by calculation using various $$$\theta$$$ angles and then normalize the reconstructions in sup norm. We plot reconstruction errors for GRAPPA and MGRAPPA, see Figure 4. Error is L2 norm of the residual images; see Figure 3.

In Vivo Results

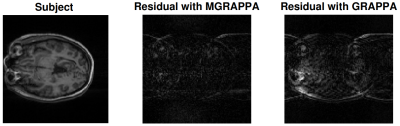
We collected full scans, 128x128, of a subject in 2 poses. We used the GRAPPA calibration data, 24*2 lines, from the first pose to reconstruct the scan from the second pose (subsample every other line and then reconstruct), both with and without MGRAPPA correction ($$$\epsilon=.05$$$). The L2-norm error decreases 41% with MGRAPPA, see Figure 5.

Discussion

While the reconstruction error with GRAPPA increases markedly with rotations in an almost linear fashion, MGRAPPA uses approximations to mitigate this and results in a stable method with consistently low errors. In vivo, this appears as less ringing and blurring in the brain image We conclude that our method has great potential to reduce re-scanning and improve image quality in the presence of motion.