1158
Accelerating Bayesian Compressed Sensing for Fast Multi-Contrast Reconstruction1Harvard University, Cambridge, MA, United States, 2Department of Radiology, Massachusetts General Hospital, Martinos Center for Biomedical Imaging, Boston, MA, United States, 3Harvard Medical School, Boston, MA, United States
Synopsis
We propose Bayesian accelerated Compressed Sensing (BaCS) to improve the computational speed of Bayesian CS by two orders of magnitude. We achieve this by circumventing a costly matrix inversion problem using conjugate gradients and Monte Carlo sampling, which lend themselves well to parallel processing using GPUs. Exploiting parallelism renders BaCS even faster than sparseMRI, while having the ability to exploit similarities between multi-contrast images to improve reconstruction performance. Further, we extend BaCS to multi-channel reconstruction by synergistically combining it with SENSE to enable yet higher acceleration rates.
Introduction
Bayesian compressed sensing (BCS) is an effective method for multi-contrast reconstruction that leverages mutual information among the multiple contrasts routinely acquired in clinical exams to achieve improved image quality [1]. A key limitation is its long computation time, often requiring multiple hours, which has restricted BCS to single-coil reconstruction. To address this, we propose a novel time-and-memory-efficient learning algorithm that accelerates BCS by two orders of magnitude. The time efficiency enables BCS to run faster than SparseMRI [2], while maintaining superior accuracy using multi-contrast reconstruction. The memory efficiency allows us to port our code to GPUs, which provide further speed boosts. As a key consequence of our speed-up, we have further extended BCS to multi-channel reconstruction.Method
Overall Idea: As described in [1] and depicted in Figure 1, BCS leverages joint sparsity in the horizontal/vertical image gradients to reconstruct $$$L$$$ contrasts at once. Let $$$y_1,y_2,\ldots,y_L$$$ denote the undersampled Fourier transforms $$$\Phi_1,\Phi_2,\ldots,\Phi_L$$$ of the $$$L$$$ gradients $$$\delta_1,\delta_2,\ldots,\delta_L$$$. Let $$$\sigma^2$$$ denote the variance of the complex Gaussian noise that corrupts $$$k$$$-space. BCS recovers a posterior distribution $$$p(\delta_i|y_i) = \mathcal{N}(\mu_i, \Sigma_i)$$$ for each contrast $$$i$$$ while learning a prior distribution $$$p(\delta_i) = \mathcal{N}(0, \text{diag}(1 / \alpha))$$$. This is done using Expectation-Maximization (EM), which alternates between the following steps:$$\mu_i = \frac{1}{\sigma^2}\Sigma_i\Phi_iy_i, \quad \Sigma_i=\left(\frac{1}{\sigma^2}\Phi_i^T\Phi_i+\text{diag}(\alpha)\right)^{-1} \quad \text{(E-Step)}$$
$$\alpha = \frac{L}{\sum_{i=1}^L\mu_i^2 + v_i} \quad \text{(M-Step)}$$
where $$$v_i$$$ denotes the diagonal elements of $$$\Sigma_i$$$. The bottleneck of this process is a matrix inversion to obtain $$$\Sigma_i$$$.
Our Contribution: The key insight in our Bayesian accelerated CS (BaCS) is that we do not need to explicitly compute $$$\Sigma_i$$$ since we only need $$$\mu_i$$$ and $$$v_i$$$ to update $$$\alpha$$$. The former can be solved for using conjugate gradients (CG) [3]. The latter can be estimated using Monte Carlo by drawing $$$P$$$ random probe vectors $$$z_1, z_2, \ldots, z_P$$$, where the independent components of each $$$z_p$$$ are either $$$-1$$$ or $$$+1$$$ with equal probability [4]. An unbiased estimate of $$$v_i$$$ is
$$\hat{v}_i = \frac{1}{P} \sum_{p=1}^P z_p \odot \Sigma_i z_p$$
where $$$\odot$$$ denotes element-wise product. Here, $$$\Sigma_i z_p$$$ can also be computed using CG [3], Importantly, running CG batch-wise for all $$$p = 1, \ldots, P$$$ can be parallelized.
After converging to mean and variance estimates $$$\mu_i, v_i$$$ for the gradients, we can use the former to solve for the images (Figure 1) and the latter to characterize the reconstruction uncertainty.
Multiple Coils: BaCS permits extension to the multi-coil setting. Following [5], we perform SENSE and BaCS in sequence by (1) uniformly undersampling the $$$k$$$-space by factor $$$R_1$$$ to create images with reduced FOV, (2) further random undersampling by factor $$$R_2$$$, (3) jointly reconstructing the reduced-FOV coil images using BaCS, and (4) running SENSE to recover the full FOV image.
Results
We compare the performance and speed of BaCS against SparseMRI [2] on several datasets. SparseMRI used sparsity penalty with optimal performance and large number of iterations to ensure convergence. For BaCS, we use 30-40 EM iterations along with 32 or 64 inner CG loops and 5-8 probe vectors. GPU experiments ran on an Nvidia T4 Tensor Core.Fig2. displays results for the two complex 128x128 Shepp-Logan phantoms in [1] at a 2D-undersampling rate of $$$R=5$$$. SparseMRI obtains an RMSE of 0.7%, while both the original BCS and proposed BaCS obtain perfect image recovery at 0.0% RMSE. SparseMRI takes 5.2min, while BCS takes 2.2min. BaCS takes 1.1min on the CPU and 6.8sec on the GPU.
Fig3. presents results for the SRI24 Atlas [6] of three 200 x 200 images undersampled at rate $$$R=4$$$ in 1D. Here, SparseMRI obtains 5.4% RMSE in 22.3min, while original BCS obtains 3.6% RMSE in 1.5hours. On the other hand, BaCS achieves the lowest RMSE of 2.9% in 2.5min. Running BaCS on GPU reduces the time further to only 14sec. This is a 36x speedup on the CPU and a 385x speedup on the GPU.
In Fig4., we run SparseMRI and BaCS on four 256x256 in-vivo complex, single-coil images (GRE, T2-Weighted, FLAIR, T1-Weighted). We sweep different 2D undersampling factors $$$R=2,3,4,5,6$$$. In all cases, BaCS outperforms SparseMRI by 1.5-2.0% RMSE (upper right), while being 2.8 times faster on the CPU and 31 times faster on the GPU (lower right). The displayed images are for acceleration factor $$$R = 4$$$.
In Fig5., we apply BaCS to the multi-coil setting to reconstruct a 256x256 in-vivo complex image with data collected from 32 coils. We use a uniform undersampling rate $$$R_1 = 2$$$ and random undersampling rate $$$R_2 = 2.5$$$ for an overall rate of $$$R = 5$$$. We compare our BaCS + SENSE reconstruction method with a standard SENSE reconstruction using $$$R = 5$$$ uniform undersampling. BaCS + SENSE achieves an RMSE of 5.7%, while SENSE alone has RMSE 8.1%.
Conclusion
In this work, we accelerated BCS by two orders of magnitude, made the learning algorithm GPU-compatible, and applied the method to multi-channel reconstruction with sensitivity encoding for the first time. Importantly, BaCS offers the additional robustness of not having free regularization parameters that need to be tuned.Future work will explore further synergies between BaCS and parallel imaging (e.g. directly incorporating coil sensitivities into the BCS forward model).
Acknowledgements
This work was supported by research grants NIH R01 EB028797, U01 EB025162, P41 EB030006, U01 EB026996 and the NVidia Corporation for computing support.References
[1] Bilgic, Berkin, Vivek K. Goyal, and Elfar Adalsteinsson. "Multi‐contrast reconstruction with Bayesian compressed sensing." Magnetic resonance in medicine 66.6 (2011): 1601-1615.
[2] Lustig, Michael, et al. "Compressed sensing MRI." IEEE signal processing magazine 25.2 (2008): 72-82.
[3] Hestenes, Magnus R., and Eduard Stiefel. "Methods of conjugate gradients for solving linear systems." Journal of research of the National Bureau of Standards 49.6 (1952): 409-436.
[4] Bekas, Costas, Effrosyni Kokiopoulou, and Yousef Saad. "An estimator for the diagonal of a matrix." Applied numerical mathematics 57.11-12 (2007): 1214-1229.
[5] Rohlfing, Torsten, et al. "The SRI24 multichannel atlas of normal adult human brain structure." Human brain mapping 31.5 (2010): 798-819.
Figures
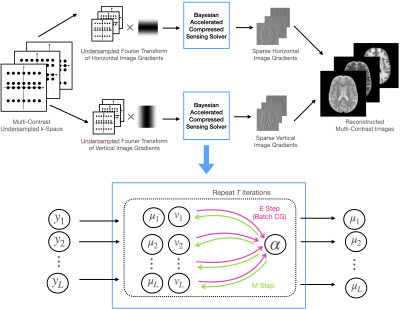
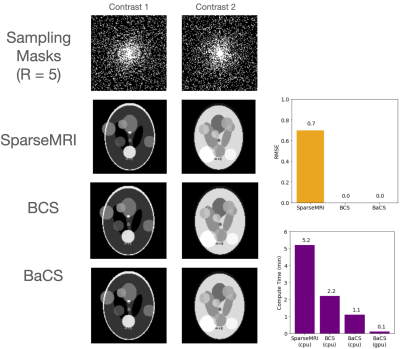
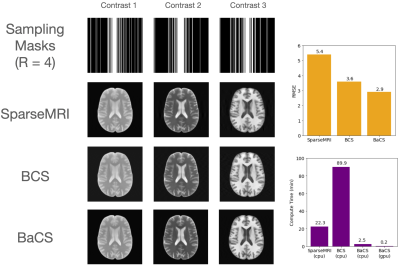
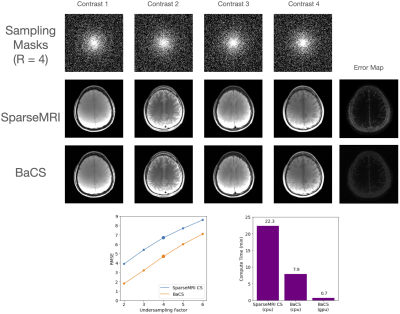
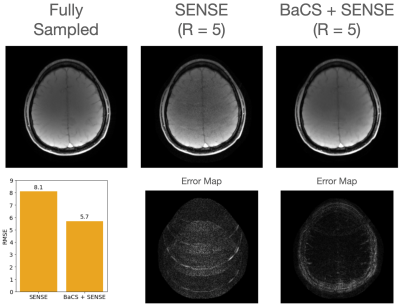
Fig5. Synergistic combination of BaCS with SENSE yields a significant, 1.4x improvement in RMSE over standard SENSE reconstruction at R=5-fold total acceleration using 32 channel data. This is made possible by the application uniform R1=2-fold undersampling with SENSE, and an additional R2=2.5-fold random undersampling on the reduced FOV coil images with joint BaCS reconstruction.