1157

Near-optimal tuning-free multicoil compressed sensing MRI with Parallel Variable Density Approximate Message Passing
Charles Millard1,2, Aaron T Hess2, Jared Tanner1, and Boris Mailhe3
1Mathematical Institute, University of Oxford, Oxford, United Kingdom, 2Oxford Centre for Clinical Magnetic Resonance Research, University of Oxford, Oxford, United Kingdom, 3Digital Technology and Innovation, Siemens Healthineers, Princeton, NJ, United States

Synopsis

We present the Parallel Variable Density Approximate Message Passing (P-VDAMP) algorithm for compressed sensing MRI, which extends the recently proposed single-coil VDAMP algorithm to multiple coils. We evaluate the performance of P-VDAMP on eight datasets at a number of undersampling factors and find that it converges to a mean-squared error similar to the Fast Iterative Shrinkage Thresholding Algorithm (FISTA) with an optimally tuned sparse weighting, but in around 5x fewer iterations and without the need to tune model parameters.

Introduction

Compressed sensing MRI1 typically requires the tuning of one or more model parameters. Parameter tuning is often done by hand, which may lead to sub-optimal image restoration. Stein's Unbiased Risk Estimate (SURE)2 has previously been employed in MRI for parameter selection3,4. However, parameter tuning via SURE is only near-optimal when the aliasing of the intermediate solution is Gaussian with a known covariance matrix.

Recently, the authors proposed the Variable Density Approximate Message Passing (VDAMP) algorithm for single-coil compressed sensing MRI5. The aliasing of the intermediate solution of VDAMP closely matches a zero-mean Gaussian distribution, so SURE tunes model parameters on-the-fly to near optimality. VDAMP was found to converge to a Mean-Squared Error (MSE) comparable with optimally tuned FISTA6 in around 15x fewer iterations on average. This abstract presents Parallel-VDAMP (P-VDAMP), which extends single-coil VDAMP5 to multiple receive coils.

Description of algorithm

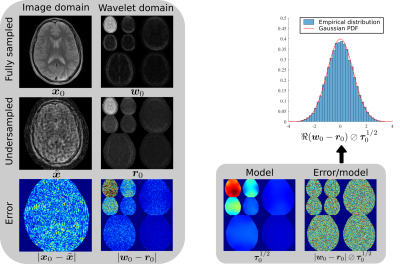
Denote the measurements on coil $$$c$$$ as $$\boldsymbol{y}_c=\boldsymbol{M}_\Omega(\boldsymbol{F}\boldsymbol{S}_c\boldsymbol{x}_0+\boldsymbol{\varepsilon}_c),$$ where $$$\boldsymbol{M}_\Omega$$$ is a measurement mask, $$$\boldsymbol{F}$$$ is a Fourier transform, $$$\boldsymbol{S}_c$$$ is the $$$c$$$th coil sensitivity and $$$\boldsymbol{\varepsilon}_c$$$ is measurement noise with variance $$$\sigma_\varepsilon^2$$$.

The P-VDAMP algorithm is shown in Fig. 1. For a detailed description of the form of P-VDAMP, see the single-coil VDAMP paper5. The role of $$$\boldsymbol{\tau}_k$$$ in line 5 is to model the covariance of the aliasing of $$${\boldsymbol{r}}_k $$$, which is approximated as diagonal in the wavelet domain: $${\boldsymbol{r}}_k\approx\boldsymbol{w}_0+\mathcal{CN}(\boldsymbol{0},\text{Diag}(\boldsymbol{\tau}_k)),$$ where $$$\boldsymbol{w}_0:=\boldsymbol{{\Psi}x}_0$$$ are the ground-truth wavelet coefficients. The accuracy of P-VDAMP's aliasing model at $$$k=0$$$ is illustrated in Fig. 2. The left-hand-side shows a tenfold undersampled brain, its image domain and wavelet domain estimates $$$\tilde{\boldsymbol{x}} = \sum_c\boldsymbol{S}_c^H\boldsymbol{F}^H\boldsymbol{P}^{-1}\boldsymbol{y}_{c}$$$ and $$$\boldsymbol{r}_{0}=\boldsymbol{\Psi}\tilde{\boldsymbol{x}}$$$, and their entry-wise errors. On the right-hand-side the aliasing model $$$\boldsymbol{\tau}_0$$$ and the normalized aliasing $$$|\boldsymbol{w}_0-{\boldsymbol{r}}_0|\oslash\boldsymbol{\tau}^{1/2}_0$$$ is shown, where $$$\oslash$$$ is entry-wise division. The normalized aliasing has the qualitative appearance of white Gaussian noise, which is quantitatively verified by the histogram in the top right, which shows the real part of $$$(\boldsymbol{w}_0-{\boldsymbol{r}}_0)\oslash\boldsymbol{\tau}^{1/2}_0$$$; the imaginary part is similar, but is not shown here for conciseness. Fig. 2 therefore demonstrates that $$${\boldsymbol{r}}_0\approx\boldsymbol{w}_0+\mathcal{CN}(\boldsymbol{0},\text{Diag}(\boldsymbol{\tau}_0))$$$ is an accurate model of the true aliasing. For $$$k>0$$$ we have found that the aliasing of $$$\boldsymbol{r}_k$$$ continues to approximately obey a zero-mean Gaussian with a covariance that is well modelled by $$$\boldsymbol{\tau}_k$$$. Parameters of the denoiser $$$\boldsymbol{g}(\boldsymbol{r}_{k};\boldsymbol{\tau}_{k})$$$ on line 6 can therefore be automatically tuned on-the-fly to approximately minimize the MSE using SURE7, resulting in a rapidly converging, tuning-free algorithm.

Method

We evaluated the performance of P-VDAMP on eight 2D datasets: three cardiac, one brain, two brain angiographies and two knee. All datasets were retrospectively undersampled with a polynomial variable density Poisson Disc at acceleration factors $$$R$$$ of 6-16 in steps of 2. The coil sensitivities $$$\boldsymbol{S}_c$$$ were estimated with ESPIRiT8 via a fully sampled $$$24\times24$$$ autocalibration region. We set P-VDAMP's damping constant $$$\rho=0.8$$$, and for the $$$\boldsymbol{c}_k$$$ update in line 8 of P-VDAMP, we used SURE to approximately minimise the mean-squared error of $$$\widetilde{\boldsymbol{r}}_k$$$: see description of VDAMP-S from the single-coil method5 for details. The aim of this experimental evaluation was to compare the performance of a number of algorithms for a given model, not to evaluate the quality of a particular model, so all comparative algorithms used the same sparse transform. For simplicity, $$$\boldsymbol{\Psi}$$$ was a Haar wavelet transform with 4 decomposition scales, and $$$\boldsymbol{g}(\boldsymbol{r}_{k};\boldsymbol{\tau}_{k})$$$ was soft thresholding with a per-subband threshold tuned on-the-fly with SURE, with cycle-spinning9.

We compared P-VDAMP with three variations of FISTA6: (1) with a near-optimal sparse weighting $$$\lambda$$$ tuned to minimise the reconstruction MSE using the ground truth, referred to as Optimal-FISTA; (2) with a sparse weighting shared across all reconstruction tasks taken as the mean of the optimal $$$\lambda$$$s, referred to as Shared-FISTA, and (3) the same SURE-based denoiser as P-VDAMP but with a scalar aliasing model, referred to as SURE-IT3.

Results

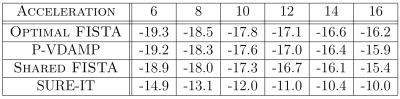
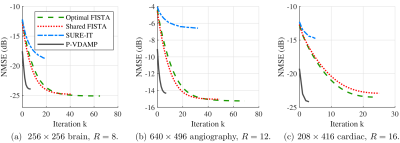
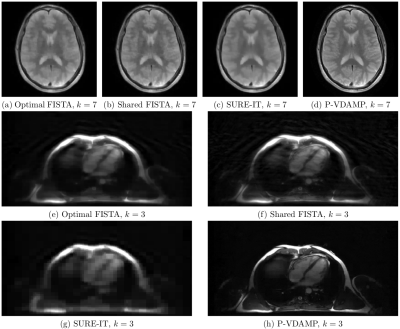
The Normalised Mean-Squared Error (NMSE) averaged over all datasets for each undersampling factor is shown in Fig.3. Averaged over all experiments, P-VDAMP converged to an NMSE 0.19dB higher than Optimal-FISTA, but 0.35dB and 5.50dB lower than Shared-FISTA and SURE-IT respectively.

The number of iterations until convergence averaged over all experiments was 26.4, 5.5, 22.7 and 7.7 for Optimal-FISTA, P-VDAMP, Shared-FISTA and SURE-IT respectively. A visualization of the relative rapidity of P-VDAMP's convergence is shown in Fig. 4, where the NMSE vs iteration for a brain, brain angiography, and cardiac reconstruction is shown at $$$R=8,12,16$$$ respectively. Fig. 5 shows the reconstruction of the brain and cardiac data at $$$k=7$$$ and $$$k=3$$$ respectively, where P-VDAMP has converged.

The required compute time until convergence was also reduced, but less substantially so due to P-VDAMP's fairly computationally demanding $$$\boldsymbol{\tau}_k$$$ update. In our MATLAB implementation, the mean time until convergence was 5.4, 4.0, 4.3 and 1.7 seconds for Optimal-FISTA, P-VDAMP, Shared-FISTA and SURE-IT respectively.

Conclusions

P-VDAMP converged to a NMSE close to optimally-tuned FISTA, but without hand-tuning of parameters, and in around 5x fewer iterations. Future work includes P-VDAMP with more sophisticated denoisers, which has been shown for single-coil measurements to give state-of-the-art image restoration10.

Acknowledgements

This work was supported in part by an EPSRC Industrial CASE studentship with Siemens Healthineers, voucher number 17000051, in part by The Alan Turing Institute under EPSRC under Grant EP/N510129/1, and in part by the BHF Centre of Research Excellence, Oxford, under Grant RE/13/1/30181.

The concepts and information presented in this abstract are based on research results that are not commercially available. Future availability cannot be guaranteed.

References

1. M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic Resonance in Medicine, vol. 58, pp. 1182–1195, 2007.

2. C. M. Stein, “Estimation of the Mean of a Multivariate Normal Distribution,” The Annals of Statistics, vol. 9, pp. 1135–1151, 1981.

3. K. Khare, C. J. Hardy, K. F. King, P. A. Turski, and L. Marinelli, “Accelerated MRi maging using compressive sensing with no free parameters,” Magnetic Resonance in Medicine, vol. 68, pp. 1450–1457, 2012.

4. F. Ong, M. Uecker, U. Tariq, A. Hsiao, M. T. Alley, S. S. Vasanawala, and M. Lustig, “Robust 4D Flow Denoising Using Divergence-Free Wavelet Transform,” Magnetic Resonance in Medicine, vol. 73, p. 828, 2015.

5. C. Millard, A. T. Hess, B. Mailhe, and J. Tanner, “Approximate Message Passing with a Colored Aliasing Model for Variable Density Fourier Sampled Images,” IEEE Open Journal of Signal Processing, p. 1, 2020.

6. A. Beck and M. Teboulle, “A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems,” SIAM Journal on Imaging Sciences, vol. 2, pp. 183–202, 2009.

7. C. Guo and M. E. Davies, “Near Optimal Compressed Sensing Without Priors: Parametric SURE Approximate Message Passing,” IEEE Transactions on Signal Processing,vol. 63, pp. 2130–2141, 2015.

8. M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, “ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA,” Magnetic Resonance in Medicine, vol. 71, pp. 990–1001, 2014.

9. R. R. Coifman and D. L. Donoho, “Translation-invariant de-noising,” Wavelets and statistics, pp. 125–150, Springer, 1995.

10. C. A. Metzler and G. Wetzstein, “D-VDAMP: Denoising-based Approximate Message Passing for Compressive MRI,” arXiv:2010.13211, 2020.

Figures

Fig. 1. The P-VDAMP algorithm. Here, $$$\langle\boldsymbol{\partial}(\boldsymbol{g}(\mathbf{r}_{k};\boldsymbol{\tau}_{k}))\rangle_\mathrm{sband}$$$ refers to the per-subband divergence, $$$\odot$$$ is entry-wise multiplication, and $$$|\cdot|$$$ is the entry-wise magnitude. In line 5, $$$\mathbf{s}_{\Delta_j}$$$ is the coil sensitivity at the shift of the jth wavelet filter and $$$p_i$$$ and $$$m_i$$$ are the ith diagonal of $$$\boldsymbol{P}$$$ and $$$\boldsymbol{M}_\Omega$$$ respectively. All vectors in line 5 have dimension equal to the number of coils.

Fig 2. The aliasing of a zero-filled, density compensated estimate in the image and wavelet domains of a tenfold undersampled brain, and the wavelet-domain aliasing estimate $$$\boldsymbol{\tau}_0$$$. The histogram verifies that $$${\boldsymbol{r}}_0 \approx \boldsymbol{w}_0 + \mathcal{CN}(\boldsymbol{0}, \text{Diag}(\boldsymbol{\tau}_0))$$$ is an accurate model of the aliasing.

Fig. 3. The mean NMSE in dB over all datasets at all acceleration factors, ordered from best to worst. Optimal FISTA was found to converge to the lowest NMSE, with P-VDAMP performing 0.19dB worse on average. P-VDAMP's NMSE was 0.35dB lower overall than Shared FISTA, where the sparse weighting was not perfectly tuned, which is more representative of model tuning in practice. P-VDAMP outperformed the other tuning-free method, SURE-IT, by 5.50dB on average, emphasizing the need for error propagation and Gaussian aliasing for effective parameter tuning with SURE.

Fig. 4. The NMSE vs iteration of three example reconstructions, demonstrating the relative rapidity of convergence of P-VDAMP. The NMSE at the 0th iteration differs because the 0th estimate is defined to be after the first application of soft thresholding.

Fig. 5. The $$$R=8$$$ undersampled brain and a $$$R = 16$$$ undersampled cardiac dataset, shown at the iteration where P-VDAMP has converged, demonstrating the relative rapidity of convergence.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)
1157