1155
Marchenko-Pastur Virtual Coil Compression (MP-VCC)1Radiology, NYU School of Medicine, New York, NY, United States
Synopsis
We propose a method of virtual coil compression using random matrix theory, MP-VCC, in which the Marchenko-Pastur distribution defines how many virtual coils may be discarded without loss beyond the PCA precision. MP-VCC is evaluated for partial Fourier, regular undersampling, and multiband acceleration.
Introduction
MRI acquisitions featuring large coil arrays provide high SNR and/or allow for high acceleration factors with in-plane parallel imaging1 and simultaneous multislice2 applications. In large multi-coil arrays, the sensitivity of an individual channel features strong spatial-localization. Therefore, for each voxel, only few out of many coil channels will contribute to the reconstructed signal. Virtual coil compression (VCC) has been introduced to compress the signal information of the multi-coil array to reduce the computational burden and suppression of thermal noise, which is present in each individual channel3,4. VCC is based on SVD across all coils, where the number of coils to keep is user dependent, without an objective criterion. This is problematic as large acceleration factors impact the minimally required number VC strongly, often in an unpredictable way5. Here we propose merging VCC with random matrix theory (RMT), an approach successfully applied for denoising via finding the low-rank structure in a set of measurements6,7, to define an objective VC cutoff for any acquisition.Methods
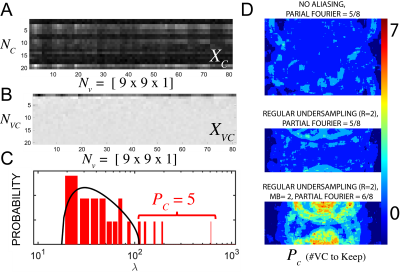
MP-VCC: Prior to VCC, we decorrelate the coil noise8 and demodulate the phase7. The mean across measurements ($$$q$$$-space in our examples) is used for high-SNR references for VCC. We define a 2d spatial kernel (patch), $$$X_C$$$, comprised of $$$N_v=[9\times\,9]$$$ voxels with $$$N_c$$$ coils, Fig.1(A). A unitary transform defined by the singular value decomposition, rotates $$$X_C$$$ into $$$X_{VC}$$$ which sorts VCs by their signal contribution, Fig.1(B). The 2d kernel for rotation is kept small to maximize spatial redundancy and minimize the number of significant VC that describe the signal. Significant signal component is defined as being above the Marchenko-Pastur9 (MP) distribution of the principal components of $$$X_{C}X_{C}'/N_v$$$, whereas MP distribution defines a range of noise-only components that may be discarded, Fig.1(C). Discarding the noisy VCs would yield nearly an SNR gain of $$$~\sqrt{P_{C}/N_c}$$$, where $$$P_C$$$ is the number of signal carrying virtual coils defined by RMT.Experiments were performed on a 3T Siemens Prisma system.
- Experiment 1: A 3-slice brain slab from a 31 y/o female volunteer was acquired with $$$1\times1\times1\,$$$mm$$$^3$$$ voxels (original SNR = 4.0 at b=0), 16-channels, TR=3s,TE=132ms, pFourier=5/8 with 8 b-shells [0,250,500,1000,2000,3000,4000,5000] along [1,6,6,12,20,30,30,40] directions, respectively. Scan time was 7min.
- Experiment 2: A 5-slice segment of the brain from a 28 y/o male volunteer with $$$0.8\times 0.8\times 0.8\,$$$mm$$$^3$$$ voxels was acquired through the hand knob of the precentral gyrus, using 16-channels, R=2, pFourier=5/8, 3 b-shells 10b=0,20b=1000,40b=2000, original SNR 3.31 at b=0. Total scan time was 3:35.
- Experiment 3: A 128-slice brain from a 47 y/o female volunteer with $$$1\times1\times1\,$$$mm$$$^3$$$ voxels was acquired using 20-channels, R=2, pFourier=6/8, MB=2, 3-bshells 11b=0, 20b=1000, 53b=2000 original SNR 3.76 at b=0. Total scan time was 19:57.
Results & Discussion
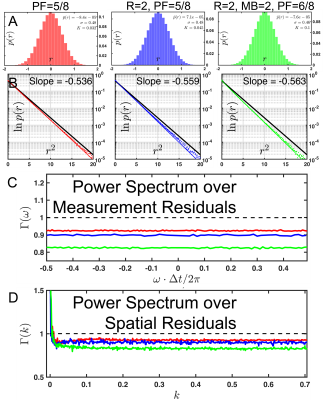
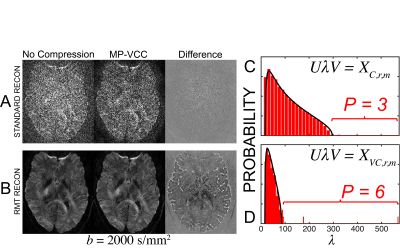
In Fig.1, we show an exemplary kernel and PCA spectrum, as well as spatially varying $$$P_C$$$ maps of the number of significant VCs for each experiment. We find that the required number of VCs is roughly proportional to the degree of aliasing. For experiment 3, Fig.1(D), the required VCs varied between 1 and 5. This indicates that VCC should be spatially varying to maximize both compression and denoising from VCC. In Fig.2 and Fig.3, we demonstrate that signal carrying VCs were not discarded using our approach. We maintain Gaussian statistics in the residuals Fig.3(A,B), with no spectral bias along the measurement dimension treated as a time-series (temporal residuals' power spectrum $$$\Gamma(\omega)$$$ is flat), and minimal spectral bias along the spatial dimension, (nearly flat power spectrum $$$\Gamma(k)$$$ of 2d spatial residuals), resembling a low-pass filter commensurate with the patch size. In Fig.4, we observe that RMT denoising7 greatly benefits from MP-VCC preprocessing. RMT reconstruction performed on MP-VCC compressed images produces DWI with sharper edges. By eliminating noise-only VCs, we reduce the number of components contributing to noise and push the RMT phase-transition10 threshold towards lower SNR. In our example, this reveals 3 additional components that were previously buried under the MP-distribution. We show that these eigenvalues correspond to edge information, as evidenced by the mean difference over all $$$b=2000\,s/mm^2$$$ between using all coils and MP-VCC in RMT reconstruction.Conclusion and Outlook
We present a data-driven/model-independent approach to determine how many VCs to keep, by merging VCC with RMT. This compression is synergistic with RMT-based reconstruction, and enhances edge information following coil-based denoising.Acknowledgements
This work was supported by the NIH under awards number R01NS088040 (NINDS) and R01EB027075 (NIBIB), and by the Center of Advanced Imaging Innovation and Research (CAI$$$^2$$$R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center: P41 EB017183.References
1. Sodickson et al. “Simultaneous acquisition of spatial harmonics (smash):Fast imaging with radiofrequency coil arrays,” Magnetic Resonance in Medicine38, 591–603 (1997),https://onlinelibrary.wiley.com/doi/pdf/10.1002/mrm.1910380414.
2. Setsompop et al. “Improving diffusion mri using simultaneous multi-slice echo planar imaging,” NeuroImage63, 569 –5580 (2012).
3. Buehrer et al. “Array compres-sion for mri with large coil arrays,” Magnetic Resonance in Medicine57, 1131–1139 (2007),https://onlinelibrary.wiley.com/doi/pdf/10.1002/mrm.21237.
4. Zhang et al. “Coil compression for ac-10celerated imaging with cartesian sampling,” Magnetic Resonance in Medicine69, 571–582 (2013),https://onlinelibrary.wiley.com/doi/pdf/10.1002/mrm.24267.
5. Muftuler et al. “Optimization of hyperparameters for sms re-construction,” Magnetic Resonance Imaging73, 91 – 103 (2020).
6. Veraart et al. “Denoising of diffusion mri using random matrix theory,” NeuroImage142, 394 – 406 (2016).
7. Lemberskiy et al. “Mri below the noise floor,” In Proceedings 28nd Scientific Meeting 0770, International Soci-ety for Magnetic Resonance in Medicine, Melbourne, Australia, 2020 (2020).
8. Roemer et al. “The NMR phased array,” Magnetic Resonance in Medicine16, 192–225 (1990).
9. Marchenko and Leonid A. Pastur, “Distribution of Eigenvalues for Some Sets of RandomMatrices,” Mathematics of the USSR-Sbornik1, 457–483 (1967).
10. Debashis Paul, “Asymptotics of sample eigenstructure for a large dimensional spiked covariance model,”25Statistica Sinica17, 1617–1642 (2007).
Figures