Introduction

Standard Diffusion-Weighted Imaging (DWI) frequently suffers from geometric distortions, severely restricting diagnostic value, e.g. in localization of breast cancer lesions. To overcome this problem, DWI based on Double-Echo-Steady-State (DESS) sequences was proposed (so-called dwDESS^1,2). However, it is yet unknown how to define a corresponding b-value, which would enable a quantitative comparison of dwDESS with other types of DWI. This study investigates the signal model previously developed^1,2 and derives an effective b-value for a bipolar version of dwDESS.³

Theory

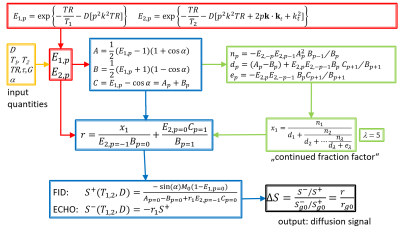
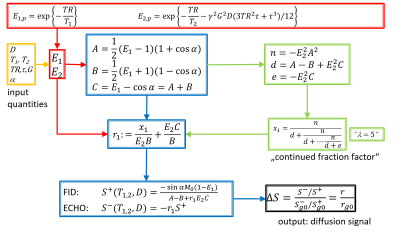
The general signal model of dwDESS in the framework of configuration theory¹ is summarized in Fig.1. Based on predefined input quantities (yellow) belonging to tissue (T₁,T₂, diffusivity D) and sequence design (repetition time TR, diffusion gradient duration τ, diffusion gradient amplitude G, flip angle α), the exponential factors E₁ and E₂ are defined (red). These factors lead to several intermediate variables (blue, green), which allow calculation of signal amplitude of FID S⁺ measured shortly after a given RF pulse and echo S⁻ measured shortly before next RF pulse. A double normalization (echo normalized by FID, ratio normalized by fixed gradient amplitude G=g0) yields the desired diffusion signal ΔS (black). Figure 2 summarizes the scenario for a bipolar diffusion gradient placed symmetrically within TR, consisting of two lobes each with duration τ/2 and opposite polarity.³ Due to this symmetry, E₁,E₂, and derived quantities simplify (particularly, mode number p completely cancels out), and so does the continued fraction factor x₁, which now can be approximated by first order terms of its numerator and denominator (Fig.3). Ideally, x₁ comprises an infinite number of levels λ, but usually converges after λ~5.^1,2 However, first order terms of numerator/denominator don't change with λ. Thus using these first order terms to approximate x₁, diffusion signal ΔS can be calculated analytically, yielding a mono-exponential function. The exponent b’ of this function reads

Eq.(1): b'=γ²G²(3TR²τ+τ³)/12

and can be used as effective b-value for dwDESS. For the limit of τ−>TR, Eq.(1) reads

Eq.(2): b’=γ²G²τ³/3

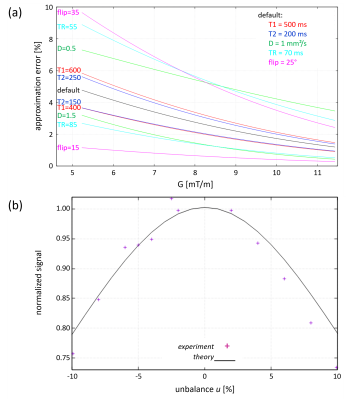
and is thus proportional to the textbook definition of b, related to standard DWI sequences. The error introduced by the approximation of x₁ depends on the input variables (G,T₁,T₂,D,TR,α) and is typically below 10% (Fig.4a).
Furthermore, the investigated bipolar version of dwDESS³ requires a small unbalance u between the two diffusion gradient lobes to suppress adverse banding artefacts,⁴ i.e., two different lobe durations δ and ε

Eq.(3a): δ=τ(0.5+u)
Eq.(3b): ε=τ(0.5-u)

In practice, u can be as small as a few percent to sufficiently suppress banding,³ thus terms in E₁ and E₂ depending on p are negligible compared to terms not depending on p. The above discussed approximation of b’ now yields (with t≡TR/2-τ/2)

Eq.(4): b'=γ²G²[t²(δ+ε)+t(δ²+ε²)+(δ³+ε³)/3+2tδε+δ²ε+δε²]

reducing to Eq.(1) for u=0. Figure 4b shows the error introduced by u.

Methods

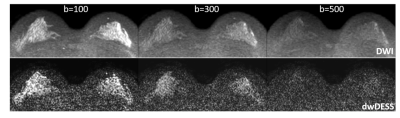
A female volunteer was measured after informed written consent obtained according to local Institutional Review Board (1.5T Ingenia, Philips Healthcare, Netherlands). Two sequences were applied, EPI-DWI (acquired voxel 1.8x1.8x3.0mm³, TR/TE=997/62ms, EPI factor=87, NSA=16 yielding roughly 20s per b-value and slice) and dwDESS (acquired voxel 1.8x1.8x2.0mm³, TR/TE1/TE2=54/5.4/48.4ms, NSA=2 yielding roughly 5s per b-value and slice). For both sequences, (effective) b-values of 100/300/500s/mm² were applied. To suppress banding artefacts, u=2.5% was chosen. The impact of u on the dwDESS signal was verified by applying the dwDESS sequences to a doped water phantom using same parameters as for in vivo, but varying u between -10% and +10%.

Results

Phantom measurements confirmed the signal reduction caused by u as expected from theory (Fig.4b). Volunteer measurements show a high agreement between DWI and dwDESS using above derived b’ (Fig.5). The resulting ADC averaged over glandular area was (1.4±0.2)x10^-3mm²/s for EPI-DWI and (1.3±0.4)x10^-3mm²/s for dwDESS.

Discussion

The estimation of ADC in the framework of dwDESS was previously performed by fitting the signal model to the measured data,⁵ thus circumventing the explicit determination of an effective b. This study derived an explicit estimation of an effective b, thus enabling also the comparison of diffusion-weighted images between different sequences, different measurements, and different scanners. Noteworthy that a consistent b-value definition is limited to the specifically analyzed bipolar dwDESS sequence, as diffusion weights strongly depend on other parameters (relaxation) in unipolar dwDESS.
The estimation of b’ involves two assumptions: (1) approximation of x₁ by first order terms, (2) unbalance u only partially integrated into signal model. However, the validity of these assumptions was confirmed by theoretical simulations as well as diffusion contrast found experimentally in vivo.

Conclusion

Estimation of effective b-values in bipolar dwDESS is possible and in good agreement with the conventional b-value of standard DWI.

Acknowledgements

The authors would like to thank Oliver Bieri and Christian Stehning for their valuable support.