Introduction

Quantitative DCE-MRI is still limited by the relatively slow imaging speed and motion sensitivity of conventional MRI and complications to obtain a robust arterial input function (AIF). This work proposes to combine the high imaging speed, reconstruction with flexible temporal resolution and motion robustness of Golden-angle Radial Sparse (GRASP) [1] and joint estimation of the parameters of a functional form of the AIF and the actual pharmacokinetic parameters in an alternating and iterative manner. The proposed fast personalized DCE-MRI technique is applied to patients with gynecological tumors [2-3].

Methods

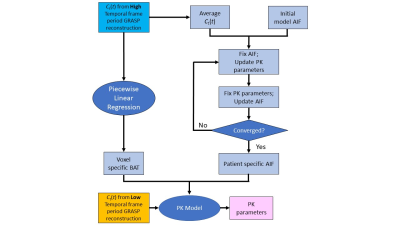
Six patients referred for routine gynecological MRI were recruited in this single institution prospective study, which is HIPAA-compliant and approved by our local institutional review board. DCE-MRI was performed using the GRASP technique with continuous golden-angle stack-of-stars acquisition and reconstruction with temporal resolutions of 1 (9 spokes/frame) and 5 seconds (45 spokes/frame). Reconstruction with 1 second temporal resolution was employed for estimation of AIF and bolus arrival time (BAT). Reconstruction with 5 seconds temporal resolution was used to estimate pharmacokinetic (PK) parameters Ktrans and ve. Joint estimation of the AIF and pharmacokinetic parameters was performed using an iterative algorithm that alternates between AIF estimation (with fixed pharmacokinetic parameters) and pharmacokinetic parameter estimation (with fixed AIF) (Fig 1). Data acquisition was performed with a 3T MRI scanner (MR750w, GE Healthcare). Monte Carlo simulations were performed over a range of temporal resolutions of (1-10 seconds) and 10% noise to assess potential measurement errors in PK parameters. Three different simulated AIF were generated as an input to the model, referred to as “Fast”, “Modulated”, and “Slow” which correspond to shape variations to the standard Parker-based population-based AIF [4]. Tissue residue curves were calculated using the Tofts PK model. Parameters estimated from the simulations were used to estimated accuracy and precision and at each setting.

Results

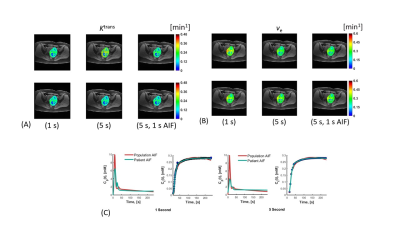
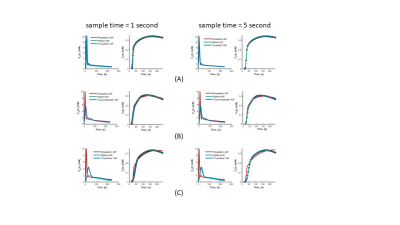
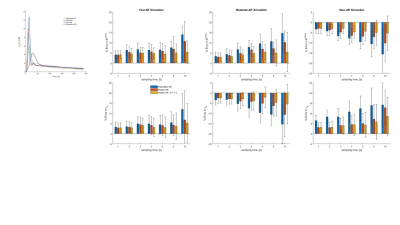
Maps of Ktrans and ve are shown in Fig. 2. Also shown are AIF and mean tissue enhancement curves, Ct(t) and the fit to the data using population based and patient-based AIF. In both cases, root-mean-squared error (RMSE) improved when patient specific AIF was used in place of the population AIF (1 s: 0.98 to 0.99; 5 s: 0.97 to 0.99). Simulation results are shown in Fig. 3 and 4. In Fig. 3, the estimated patient AIF in all cases closely matches the “True” AIF which translates to an improvement in fit of the corresponding tissue enhancement curves. Estimated fit from patient-AIF was superior and the parameters returned (Ktrans = 0.13 min-1, ve = 0.31 min-1) are identical to the values used to construct the simulated curve. In Fig. 4, the % error in estimation of Ktrans and ve are shown for the three shapes of AIF at the 1 and 5 s sampling rates. As expected, the error increases as sampling time of the data increases, for all AIF. However, when the AIF is sampled at a high sampling rate (1 second), regardless of the sampling rate of the analysis, the error in estimation plateaus and in all cases, estimated Ktrans and ve were within 10% of the high sampling rate of 1 s. The improvement in accuracy is more noticeable for lower sampling rates of 6 and 10 s. Depending on the shape of the AIF, the parameters are over- or underestimated. For “Slow” AIF, Ktrans are underestimated, whereas for “moderate” AIF, ve is underestimated. In all other cases, the values are overestimated. In summary, the simulation demonstrated that by use of a patient specific AIF: 1) Accuracy of PK parameters values (Ktrans, ve) is improved; 2) RMSE is improved; 3) the flexibility in reconstruction of data at a temporal resolution of choice, afforded by GRASP technique, allows the PK analysis to be performed such that the more suitable temporal resolution data be used in the AIF phase and parameter estimation phases of the analysis.

Discussion

Previous studies have confirmed the value of accurate AIF estimation to obtain accurate and precise estimation of pharmacokinetic parameters. The approach presented in this study allows for personalized estimation of AIF at a temporal resolution which can be the same or different that the temporal resolution used to generate data for the quantitative PK analysis. Simulations suggest that personalized AIF are more accurate that a standard population AIF, and that accuracy increases when such measurements are obtained at high temporal resolutions.

Acknowledgements

No acknowledgement found.