1030
Comparative analysis of indentation and magnetic resonance elastography for measuring viscoelastic properties1Institute for Medical Imaging Technology, School of Biomedical Engineering, Shanghai Jiao Tog University, Shanghai, China, 2Department of Radiology, Ruijin Hospital, Shanghai Jiao Tong University School of Medicine, Shanghai, China
Synopsis
Comparing viscoelastic properties of soft tissues measured in vivo and ex vivo are of interests for basic science and clinical translation. Magnetic resonance elastography (MRE) and indentation are two commonly used techniques for measurement of tissue viscoelasticity. In this study, we used a gelatin phantom to compare measurements by MRE and indentation. Using 2nd-order Prony series, frequency response measured from indentation was estimated. We observed apparent frequency-dependent behaviors from MRE in the range of 50-100 Hz, but not from indentation. Results implied that MRE and indentation measures at different frequency ranges.
Introduction
Viscoelastic properties of soft tissue were traditional measured using indentation or rotational rheometry.1,2 Magnetic resonance elastography (MRE), as a non-invasive method, is clinically used for in vivo measurement of viscoelasticity.3,4 Many comparative studies were conducted between rheometry and MRE for in vivo measurement verification. 5-7 However, few studies have compared measurement between MRE and indentation. In this study, we used 2nd-order Prony series to analyze the frequency response of a gelatin phantom based on indentation test. The results were compared with that from a multi-frequency tests of MRE.Methods
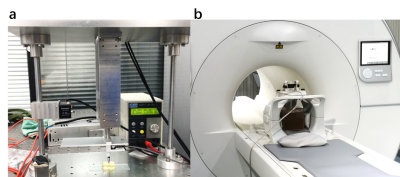
Gelatin phantoms mimicking soft tissues were measured using a ramp-hold indentation protocol (Figure 1a).8 Viscoelastic properties were estimated by fitting the relaxation curve using 2nd-order Prony series:$$ G(t) = C_0 + C_1·e^{-\frac{t}{\tau_{1}}} + C_2·e^{-\frac{t}{\tau_{2}}}, $$
where and are viscoelastic parameters.
A custom-built magnetic resonance elastography (MRE) system was used for measuring the dynamic moduli of the phantom 9. The experiments were performed on a 3T MRI scanner (uMR 790, United Imaging Healthcare, Shanghai, China). (Figure 1b). The measured frequencies ranged from 50 to 100 Hz with a 10Hz step. A spin echo-EPI sequence was used for imaging, with TR/TE=1000/48 ms,FOV=300x300 mm2, a matrix size of 127x127, and a slice thickness of 5 mm. Dynamic shear modulus measured from MRE were estimated by both local frequency estimation (LFE) and direction inversion (DI).
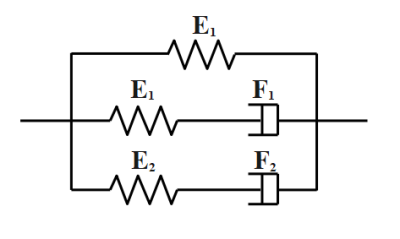
To analyze the frequency response of the model estimated from indentation, we convert the 2nd-order Prony series into a 5-parameter Maxwell model (Figure 2). The model parameters were determined based on the physical interpretation of the Prony series:
$$ E_1 = 3C_0, E_2 = 3C_1, E_3 = 3C_{2}, $$
$$ F_2 = 3\tau_{1}C_1, F_3 = 3\tau_{2}C_{2}. $$
If incompressibility was assumed, the dynamic shear modulus can be determined by . For a 2nd-order linear viscoelastic model 10,
$$ E(i\omega) = \frac{-q_{2}\omega^{2} + iq_{1}\omega + q_{0}}{-p_{2}\omega^{2} + ip_{1}\omega + 1} $$
where and were linear viscoelastic model parameters.
Therefore, by comparing the Laplacian transformation of the constitutive equation of the 5-parameter model with the analytical dynamic shear modulus, the linear viscoelastic model parameters and can be determined:
$$ q_2 = 3\tau_{1}\tau_{2}(C_0 + C_1 + C_2), q_1 = 3C_0\tau_1 + 3C_0\tau_2 + 3C_1\tau_1 + 3C_2\tau_2, $$
$$ q_0 = 3C_{0}, p_2 = \tau_{1}·\tau_{2}, p_1 = \tau_{1} + \tau_{2}. $$
Results and Discussion
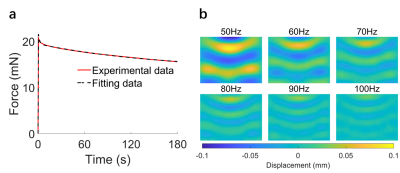
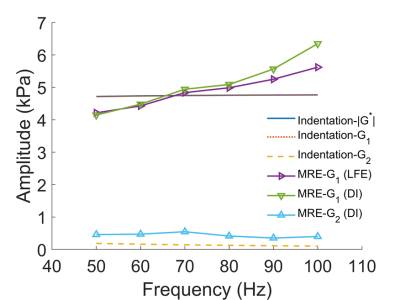
The typical ramp-hold relaxation curve from the indentation tests is shown in Figure 3a. The Wave propagation images from the MRE tests with 6 different actuation frequencies are shown in Figure 3b. A quantitative comparison of viscoelastic properties is shown in Figure 4. In the frequency range of 50-100 Hz, the result of MRE showed an apparent frequency-dependent behavior. The measured shear moduli increased with the vibration frequency increased. However, in the same frequency range, no such behavior was observed based on the indentation test. The differences in the frequency response between the MRE and indentation tests indicated the considerable influences of boundary conditions and loading conditions. Since the calculation of shear modulus in indentation test was based on , the different frequency responses of shear modulus between MRE and indentation implied that the Poisson’s ratio could be frequency-dependent, too.Conclusion
In this study, we analyzed and compared the viscoelastic parameters estimated from indentation and MRE. Both Indentation and MRE tests were used to measure the dynamic responses of viscoelastic soft tissues. The former is more prone to capture the low-frequency range response, while the latter is better for describing the response at a relatively higher frequency range. The results could provide helpful information for the ex vivo and in vivo measurements of soft tissues.Acknowledgements
Funding support from grant 31870941 from National Natural Science Foundation of China (NSFC) and grant 1944190700 from Shanghai Science and Technology Committee (STCSM) are acknowledged. We thank the technical support from Jiayu Zhu, Xiaomao Gong, Cong Zhang, Xiaodong Zhou, and Qiang He from United Imaging Healthcare, Shanghai.References
1. Li Y, Deng J, Zhou J, Li X. Elastic and viscoelastic mechanical properties of brain tissues on the implanting trajectory of sub-thalamic nucleus stimulation. J Mater Sci Mater Med 2016;27(11):163. doi: 10.1007/s10856-016-5775-5
2. Cirka HA, Koehler SA, Farr WW, Billiar KL. Eccentric rheometry for viscoelastic characterization of small, soft, anisotropic, and irregularly shaped biopolymer gels and tissue biopsies. Ann Biomed Eng 2012;40(8):1654-1665. doi: 10.1007/s10439-012-0532-5
3. Bunevicius A, Schregel K, Sinkus R, Golby A, Patz S. REVIEW: MR elastography of brain tumors. NeuroImage: Clinical 2020;25:102109. doi: https://doi.org/10.1016/j.nicl.2019.102109
4. Garteiser P, Doblas S, Van Beers BE. Magnetic resonance elastography of liver and spleen: Methods and applications. NMR in Biomedicine 2018;31(10):e3891. doi: https://doi.org/10.1002/nbm.3891 5. Klatt D, Friedrich C, Korth Y, Vogt R, Braun J, Sack I. Viscoelastic properties of liver measured by oscillatory rheometry and multifrequency magnetic resonance elastography. Biorheology 2010;47:133-141. doi: 10.3233/BIR-2010-0565
6. Dittmann F, Hirsch S, Tzschätzsch H, Guo J, Braun J, Sack I. In vivo wideband multifrequency MR elastography of the human brain and liver. Magnetic Resonance in Medicine 2016;76(4):1116-1126. doi: https://doi.org/10.1002/mrm.26006
7. Vappou J, Breton E, Choquet P, Goetz C, Willinger R, Constantinesco A. Magnetic resonance elastography compared with rotational rheometry for in vitro brain tissue viscoelasticity measurement. Magnetic Resonance Materials in Physics, Biology and Medicine 2007;20(5):273. doi: 10.1007/s10334-007-0098-7
8. Chen Y, Qiu S, Wang C, Li X, Tang Y, Feng Y. Measurement of viscoelastic properties of injured mouse brain after controlled cortical impact. Biophysics Reports 2020. doi: 10.1007/s41048-020-00110-1 9. Feng Y, Zhu M, Qiu S, Shen P, Ma S, Zhao X, Hu C-h, Guo L. A multi-purpose electromagnetic actuator for magnetic resonance elastography. Magnetic Resonance Imaging 2018;51:29-34. doi: https://doi.org/10.1016/j.mri.2018.04.008
10. Qiang B, Greenleaf J, Oyen M, Zhang X. Estimating material elasticity by spherical indentation load-relaxation tests on viscoelastic samples of finite thickness. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2011;58(7):1418-1429. doi: 10.1109/TUFFC.2011.1961
Figures