Introduction

MRE is a valuable technique to quantify mechanical properties of tissues based on the characteristics of shear waves propagation. Conventionally, motion encoding gradients (MEG) oscillating at the same frequency as the mechanical excitation are applied between RF excitation and signal acquisition to encode spins motion during wave propagation¹. Therefore, multifrequency data is usually obtained by sequentially repeating monochromatic wave excitations experiments at different frequencies. Multifrequency MRE results, fitted to a powerlaw, allow the characterization of the microstructure of tissues².
High frequency MEGs are difficult to reach due to slew rate limitations of the gradient system and low frequency MEGs induce long TEs, yielding magnitude images with low SNR.
There are however other motion encoding methods that do not use MEGs. For instance, in previous studies we demonstrated the ability of OC-based RF pulses to perform MRE³. Here in this study, we propose the use of OC RF pulses to simultaneously encode a dual-frequency shear wave, overcoming the mentioned limitations of high and low frequencies. Phantom experiments were carried out to compare conventional sequential monofrequency MRE to this simultaneous multifrequency OC-based MRE method.

Methods

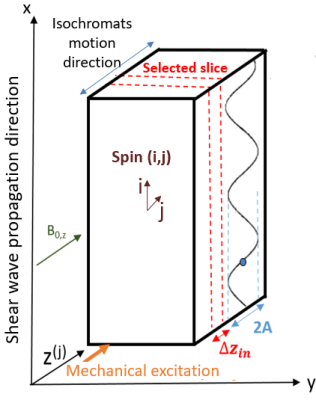
Optimal control theory was applied to MRE to design the optimized RF pulses. The computation is performed with the GRAPE algorithm⁴. The OC algorithm provides the control parameter (OC pulse) which manipulates the isochromats from the equilibrium state towards a desired target state. Bloch equations are used to simulate magnetization trajectories.
The RF pulse is simultaneously applied with a constant gradient to perform slice selectivity while a dual-frequency (f₁,f₂) shear wave produces static field variations given by ΔB₀^(i,j)(t)=G($$$\sum_{k=0}^2$$$[A_ksin(-2πf_kt+θ⁽ⁱ⁾)]+z^(j)), where z^(j) represents the isochromat (i,j) location in the slice (Figure 1). Different target states are attributed whether the isochromat is located in the slice (Δz_in) or out of the slice (Δz_out). The isochromats phase is directly linked to the phase of the wave motion they are undergoing⁵: $$$\vec{T}^{(i,j)}=\rho(cos\phi^i,sin\phi^i,0)$$$ if j$$$\inΔz_{in}$$$, $$$\vec{T}^{(i,j)}=\rho(0,0,1)$$$ if j$$$\inΔz_{out}$$$.
OC dual-frequency was compared to the classical MRE method. All the experiments were carried on a 75% plastisol (polyvinyl chloride particles in a liquid plasticizer) phantom with relaxation times values [T1,T2]=[420,35]ms. MRI measurements were performed on a preclinical Bruker 7T MRI-system with modified RARE sequences. For the OC technique, the pulse was optimized for excitation frequencies of 400 and 600Hz, a 30ms T2, a duration of 20ms, a maximum amplitude of 94μT, a bandwidth of 7kHz and a constant gradient of 164mT/m. For the conventional MRE, MEGs with 261mT/m maximum amplitude were added. The fixed parameters were: TR=1500ms, RARE factor=4, slice thickness=1mm, FOV=40x40mm², matrix size=128x128. Shear waves at 400 and 600Hz were generated with a piezoelectric actuator (CEDRAT Technologies) with equal relative amplitudes. They were separately sent during sequential monofrequency acquisitions and simultaneously for the multifrequency acquisition. More details are shown in Table 1. Two acquisitions with inversion of the MEG polarity were acquired for phase images subtraction and removal of static phase offsets.
The temporal Fourier transform was applied to the multifrequency acquisitions dataset along the phase offsets direction to separate the different frequency components. Separate inversions were then performed using a 2D Helmholtz algorithm to determine the viscoelastic parameters for each frequency.
In order to validate the motion encoding efficacy, the Phase-to-Noise Ratio (PNR) was compared among all acquisition modes (mono- and dual-frequency excitations). PNR was defined as the ratio between the average value of phase encoding in presence of mechanical excitation (Δ) and the phase encoding in its absence (σ) (PNR=Δ/σ)³. Shear storage modulus (G’) were also computed for comparison.

Results

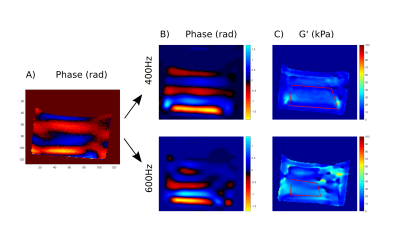
The phase image of the dual-frequency excitation is shown in Figure 2A, as well as phase images obtained from the separation of the two frequency components after temporal Fourier transform (Figure 2B). All vibrations are correctly encoded. Likewise, the G’ elastograms are computed for each excitation frequency. ROIs chosen for the analysis are also shown on the maps (Figure 2C). Table 1 summarizes Δ, σ, PNR and the mean and the standard deviation values of G’ calculated for the different excitation frequencies and acquisition modes.

Discussion and Conclusion

The PNRs are of the same order of magnitude for the different acquisition modes. Shear waves patterns obtained with the OC pulse (Figure 2B) correspond well to those found with the classical MRE. A good match is found between classical and OC strategies for the 600Hz G’ mean value. However, it is underestimated for 400Hz with OC.
A gain in time is obtained with the multifrequency OC method since only 7 phase offsets are acquired, compared to the 8 needed to repeat two monofrequency acquisitions with 4 phase shifts. It could be possible to apply an undersampling method in order to further reduce the total acquisition time.
Although the underestimation of G’ at 400Hz need to be further investigate, we demonstrated the ability of OC-based pulses to simultaneously encode two frequencies without the application of oscillating MEGs. This could overcome the limitation for high frequencies due to the slew rate of the gradient system and as we have short TEs, we could encode motion of low frequencies while preserving the SNR.
The application of OC pulses to perform multifrequency MRE with more than two frequencies is being studied.

Acknowledgements

This work was performed within the framework of the LABEX PRIMES (ANR-11-LABX-0063) of Université de Lyon, within the program "Investissements d'Avenir" (ANR-11-IDEX-0007) operated by the French National Research Agency (ANR). Experiments were performed on the PILoT platform, member of France Life Imaging infrastructure (ANR-11-INBS-0006).