Introduction

Magnetic Resonance Elastography (MRE) is a phase-contrast MRI technique that allows non-invasive assessment of tissue mechanical properties by imaging the propagation of shear waves through a tissue of interest¹. In MRE, inversion algorithms convert the acquired wave propagation images to the desired mechanical property estimates. Most inversion algorithms assume that the underlying tissue is homogeneous², or are regularized in a way that promotes piecewise-constant material property estimates³. We have recently shown that a machine-learning inversion algorithm with an inhomogeneous material property assumption offers improved resolution over algorithms assuming homogeneity⁴. The impact of the type of inhomogeneity assumption on in vivo stiffness estimates, and the influence of that choice on exam repeatability and observed biological effects, is unknown. In this study we leverage the flexibility of the machine learning inversion framework to train algorithms on simulated wave data with four different underlying material spatial property assumptions: homogeneous, piecewise constant, smooth, or piecewise smooth. The four inversion algorithms are evaluated in a brain simulating phantom with stiff inclusions, a test-retest repeatability dataset, and an Alzheimer’s disease dataset. We hypothesize that the most complex assumption – piecewise smooth material properties – will produce the highest inclusion contrast in the phantom and will be most sensitive to biological effects in the Alzheimer’s disease dataset, as it encompasses the widest range of possible wave behavior.

Methods

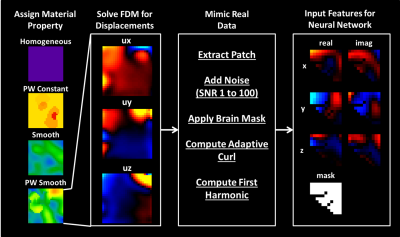
Training data: Simulated datasets were generated using a finite difference model (FDM) of the governing equation of motion for linear, elastic, isotropic materials in response to a harmonic driving force:
$$∇∙[ μ ( ∇u+(∇u) ^T )+ λ(∇∙u)I]=-ρω^2 u$$
where u is displacement, µ and λ are Lamé parameters, ρ is density, and ω is frequency. The FDM assumed near incompressibility (Poisson’s ratio of 0.49) and was solved using 30,000 iterations of the conjugate gradient method. Each simulation was a 34x34x34 cube at 3mm isotropic resolution with fixed boundaries and 1-10 60Hz harmonic force generators with randomly assigned x, y, and z components placed one voxel off the boundary. Simulated stiffness and damping ratio values ranged from 0.5-5kPa and 0-0.7 respectively. Smoothly varying components of material property maps were generated by smoothing uniformly distributed random noise with 3D Gaussian kernels of variable dimensions. A random-walk algorithm with subsequent dilations and erosions was used to produce a variety of convex and non-convex inclusion shapes and sizes.
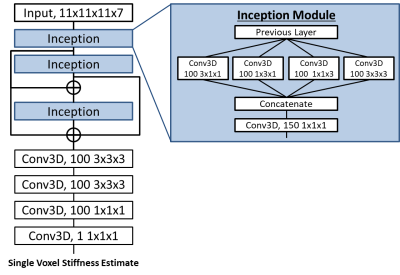
Learned Inversion Framework: All models were trained on 11x11x11 voxel training patches extracted from the larger simulated examples. Each patch passed through pre-processing steps to mimic our real data processing pipeline (Figure 1). The output of the neural network (architecture in Figure 2) is the stiffness of the voxel at the center of the training patch.
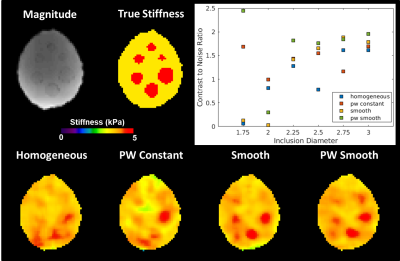
Phantom: The brain simulating phantom is made of PVC gel inside of a PVC skull with a background stiffness of ~3.4 kPa and inclusion stiffness of ~7.1 kPa. The phantom was scanned at 2mm isotropic resolution at 60Hz vibration frequency as previously reported4. The phantom data was resampled to 3mm isotropic resolution to allow use of the same inversion algorithms on the phantom and in vivo data. The contrast to noise ratio (CNR) is reported for each inclusion with each inversion.
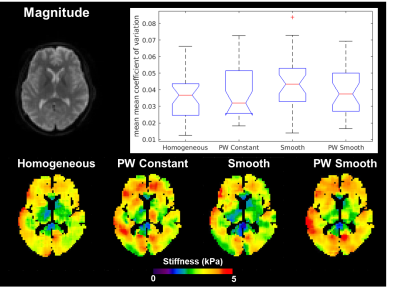
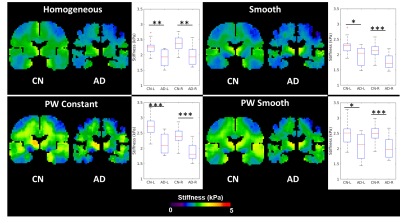
In Vivo Brain Data: All included brain MRE data comes from previously published studies, and was acquired at 3mm isotropic resolution and 60Hz vibration frequency. A test-retest repeatability dataset⁵ was used to evaluate the impact of inversion choice on exam repeatability, and an Alzheimer’s disease (AD) dataset⁶ was used to evaluate the impact on an observed biological effect in a diffuse disease. In the test-retest repeatability study, the coefficient of variation (CV) is calculated in 35 gray matter regions of interest (ROIs) derived from a previously published T1-weighted imaging based segmentation pipeline⁵. Differences in CV for each ROI are evaluated using a one-way ANOVA. In the AD study, differences in stiffness between 32 cognitively normal (CN) controls and 8 AD subjects were evaluated in left and right medial temporal lobe gray matter ROIs using a generalized linear model (response variable: stiffness, prediction variables: disease status, age, and sex).

Results

The piecewise smooth inversion algorithm produced stiffness estimates with the highest CNR for inclusions in the brain simulating phantom (Figure 3). Example stiffness maps in a single subject from the repeatability study are shown in Figure 4. There was no significant difference in the CV between inversions in any of the 35 gray matter ROIs. All four inversion algorithms detected a stiffness decrease in medial temporal lobe gray matter in the AD subjects (Figure 5).

Conclusions

This study evaluated the impact of an inversion’s assumed material property on stiffness estimates in MRE for inversions with a 3.3x3.3x3.3cm spatial footprint. The piecewise smooth inversion algorithm provided the highest CNR in the phantom, matching our observation with a different simulation model⁴. While in vivo stiffness maps changed appreciably with each inversion algorithm, inversion material property assumption had no impact on test-retest repeatability or sensitivity to softening of the medial temporal lobe in Alzheimer’s disease. Future work will assess the impact of inversion material property assumption in focal lesions, where the phantom result suggests the difference in performance may be more significant.