1019

Optimal multiple motion encoding in phase contrast MRI

Helge Herthum¹, Hugo Carrillo², Axel Osses², Sergio Uribe³, Ingolf Sack¹, and Cristóbal Bertoglio⁴
¹Experimentelle Radiologie, Charité Universitätsmedizin Berlin, Berlin, Germany, ²Center for Mathematical Modeling, Universidad de Chile, Santiago, Chile, ³Department of Radiology, School of Medicine, Pontificia Universidad Católica de Chile, Santiago, Chile, ⁴Bernoulli Institute, University of Groningen, Groningen, Netherlands

Synopsis

Optimal multiple motion encoding (OMME) for phase-contrast MRI was developed with application to magnetic resonance elastography for unwrapping motion images. OMME is formulated as a least-squares problem using multiple phase-contrast measurements with different motion encoding gradients (MEG). OMME is applied to phantom and in vivo human brain experiments. The wrap-free motion images are further used to reconstruct shear-wave-speed maps and compared to conventional phase unwrapping methods. OMME generates wrap free phase-contrast images with the wrap limit determined by the smallest MEG used, while maintaining the signal-to-noise ratio(SNR) of the largest MEG, which makes OMME especially suitable for high SNR applications.

Introduction

In magnetic resonance elastography(MRE), harmonic motion is encoded in the phase of the complex MR signal proportional to the encoding efficiency of the motion encoding gradient (MEG)[1-3]. Because the phase can only be measured in the half-open interval [-pi,pi), phase wraps occur if the encoded phase exceeds this limit. Unfortunately, selecting a large dynamic range leads to poor quality images since the “motion-to-noise-ratio"(MNR) in the phase image is inversely proportional to the dynamic range.
Phase wraps can be removed by unwrapping algorithms, which may fail if the wrapped regions are highly heterogeneous or noisy. The true motion cannot be recovered[4].
Another possibility is voxelwise motion reconstruction using dual-encoding strategies, which are based on unwrapping low dynamic-range data by exploiting high-dynamic range data[5-7] at the cost of additional measurements. We extended the mathematical framework of optimal dual-encoding to optimal multiple motion encoding(OMME). The basic idea of OMME is to include additional measurements with larger MEGs while keeping the dynamic range of the motion-sensitive phase image large. OMME presents a superior performance with respect to noise compared to standard dual encoding unwrapping and succeeds where other methods fail.
Applying the OMME method to MRE allows obtaining high motion-to-noise ratio wrap-free phase-contrast images. Reconstructed shear wave speed maps show better detail resolution by overcoming the unwrapping problem.

Theory and methods

OMME is formulated as a least-squares problem for the motion using an arbitrary number of phase-contrast measurements N with different motion encoding gradients (MEG) with corresponding dynamic range , i.e. the inverse of the encoding efficiency. The global minimization of the cost functional J gives the multiple motion encoding reconstruction u*.
$$J_N (u) = \sum_{j=1}^N \left( 1 - \cos\left( \frac{\pi}{d_j} (u_j - u)\right) \right),$$
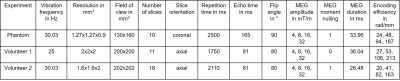
OMME’s performance was assessed on MRE data from heparin phantom experiments and two vivo human brain experiments for the most robust MEG combination obtained by the theory. The imaging parameters for the single-shot, spin-echo EPI sequence at the 3T Siemens Magnetom Lumina scanner are given in Table 1. OMME offers wrap-free phase images with MNR corresponding to the largest MEG used for OMME phase recovery. To calculate MNR for experimental data we used the blind noise estimation method of Donoho et al.[8].
The unwrapped wave images were further used to reconstruct shear-wave-speed(SWS) maps based on phase-gradient wavenumber recovery k-MDEV[9] and compared to the ones obtained using conventional phase unwrapping methods like Flynn[10] and Laplacian[11] unwrapping. Original k-MDEV was adapted to the brain by replacing the linear radial filter in the spatial frequency domain by a radial bandpass Butterworth filter (third order, highpass threshold:15 1/m, lowpass threshold:250 1/m).

Results

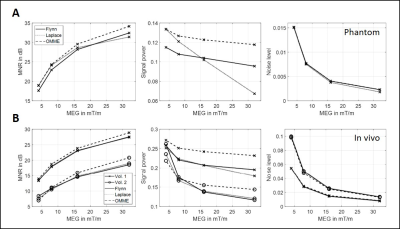
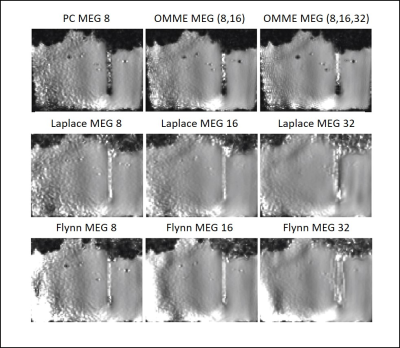
Figure 1 shows the results of the noise analysis for the phantom and in vivo data for the wrap-free phase images recovered from Laplacian, Flynn and OMME based unwrapping. MNR increases with increasing MEG as noise levels decrease as predicted by theory. OMME based unwrapping outperforms the other methods in terms of MNR.
Figure 2 presents the waves for the phase contrast cases and OMME. The dynamic range for the phase contrast images lowers as MEG increases, resulting in more wraps. The OMME methods show the dynamic range of the smallest MEG and are fully unwrapped.
Figure 3 presents SWS maps obtained by single and OMME reconstructions compared with Laplace and Flynn unwrapping applied to the single encoding images. The SWS maps are more homogeneous towards the center of the phantom and noisier far from the probe. Increasing the MEG reduces the noise in the SWS maps. Both conventional phase unwrapping algorithms exhibit different drawbacks. Laplacian based unwrapping smooths image details as it can be seen from the disappeared air inclusions in the reconstructed SWS map for the phantom data. The inclusions also disappear with Flynn since it cannot solve correctly the phase jump at the air-heparin boundary.
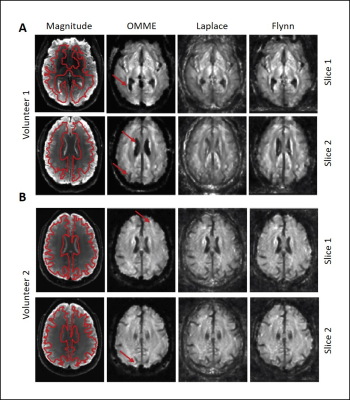
Figure 4 shows SWS maps for volunteer 1 and 2, reconstructed from OMME phase images using four MEGs, and Laplacian based unwrapping as well as Flynn unwrapping with the strongest MEG. MRE magnitude images are shown for anatomical reference. Red arrows indicate areas where OMME based reconstruction shows higher level of details than unwrapping procedures by fully recovering fluid/tissue boundaries between brain tissue and either ventricles or gyri. The transition between the skull and the brain tissue is also properly reconstructed, while the unwrapping methods smooth that region leading to spurious stiffness values.

Discussion

OMME allowed to successfully combine three and four MRE wave images with different dynamic ranges in the phantom and volunteer data, respectively. This leads to improved motion-to-noise ratio (MNR) in the measured waves and therefore to SWS maps with greater resolution of details than obtained with conventional unwrapping methods. While conventional unwrapping methods perform well for a lower amount of phase wraps, thus low MNR, OMME extends the dynamic range in phase contrast MRI towards high-MNR wrap-free motion encoding.

Conclusion

The proposed OMME method allows for an effective increase in the dynamic range of phase-contrast images with respect to the number of MEGs while maintaining the MNR of the image with the lowest dynamic range. The method may be especially suitable for applications where high-resolution MRE images with high MNR are needed.

Acknowledgements

H.H. and I.S. acknowledge the funding from the German Research Foundation (GRK 2260 BIOQIC, SFB1340 Matrix inVision) and from the European Union’s Horizon 2020 Program (ID 668039, EU FORCE – Imaging the Force of Cancer). C.B. acknowledges the funding from the European Research Council (ERC) under the European Union’s Horizon 2020research and innovation programme (grant agreement No 852544 - CardioZoom). A.O. acknowledge the funding of Conicyt Basal Program PFB-03, Fondecyt 1151512 and Fondap CR2-1511009. A.O and S.U. acknowledge funding from ANID Millennium Science Initiative Program – NCN17–129.

References

1 Hirsch, S., Braun, J. & Sack, I. Magnetic Resonance Elastography: Physical Background And Medical Applications. (Wiley-VCH, 2017).

2 Singh, S., Venkatesh, S. K., Wang, Z., Miller, F. H., Motosugi, U., Low, R. N., Hassanein, T., Asbach, P., Godfrey, E. M., Yin, M., Chen, J., Keaveny, A. P., Bridges, M., Bohte, A., Murad, M. H., Lomas, D. J., Talwalkar, J. A. & Ehman, R. L. Diagnostic Performance of Magnetic Resonance Elastography in Staging Liver Fibrosis: A Systematic Review and Meta-analysis of Individual Participant Data. Clin Gastroenterol Hepatol (2014).

3 Klatt, D., Hamhaber, U., Asbach, P., Braun, J. & Sack, I. Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: A study of brain and liver viscoelasticity. Phys Med Biol 52, 7281–7294 (2007).

4 Barnhill, E., Kennedy, P., Johnson, C. L., Mada, M. & Roberts, N. Real-time 4D phase unwrapping applied to magnetic resonance elastography. Magn Reson Med, [Epub ahead of print] doi: 10.1002/mrm.25332 (2014).

5 Carrillo, H., Osses, A., Uribe, S. & Bertoglio, C. Optimal Dual-VENC Unwrapping in Phase-Contrast MRI. IEEE Trans Med Imaging 38, 1263-1270, doi:10.1109/tmi.2018.2882553 (2019).

6 Lee, A. T., Pike, G. B. & Pelc, N. J. Three-point phase-contrast velocity measurements with increased velocity-to-noise ratio. Magn Reson Med 33, 122-126, doi:10.1002/mrm.1910330119 (1995).

7 Yin, Z., Sui, Y., Trzasko, J. D., Rossman, P. J., Manduca, A., Ehman, R. L. & Huston, J., 3rd. In vivo characterization of 3D skull and brain motion during dynamic head vibration using magnetic resonance elastography. Magn Reson Med 80, 2573-2585, doi:10.1002/mrm.27347 (2018).

8 Donoho, D. L., Johnstone, I. M., Kerkyacharian, G. & Picard, D. Wavelet shrinkage: asymptopia? Journal of the Royal Statistical Society: Series B (Methodological) 57, 301-337 (1995).

9 Tzschatzsch, H., Guo, J., Dittmann, F., Hirsch, S., Barnhill, E., Johrens, K., Braun, J. & Sack, I. Tomoelastography by multifrequency wave number recovery from time-harmonic propagating shear waves. Med Image Anal 30, 1-10, doi:10.1016/j.media.2016.01.001 (2016).

10 Flynn, T. J. Two-dimensional phase unwrapping with minimum weighted discontinuity. JOSA A 14, 2692-2701 (1997).

11 Schofield, M. A. & Zhu, Y. Fast phase unwrapping algorithm for interferometric applications. Optics letters 28, 1194-1196 (2003).

Figures

MNR (left), signal power (center) and noise (right) levels estimated from wavelet decomposition for all MEG strengths with Flynn and Laplacian unwrapping and OMME for A) phantom data and B) in vivo data. Signal and noise levels were averaged over all slices and components. For OMME, the data points indicate largest MEG used, i.e. at MEG 8, OMME used MEG 8 and 4 mT/m; at MEG 16, OMME used MEG 16, 8 and 4 mT/m; at MEG 32, OMME used MEG 32, 16, 8 and 4 mT/m.

Multiple motion encoding reconstruction in the phantom for two MEGs 8 and 16 mT/m and three MEGs 8, 16 and 32 mT/m in comparison to phase contrast images. Color scale is set in the interval 80% of the dynamic range of the MEG=8 image. Large positive values are colored in yellow and negative values in blue, while green being zero. The bottom left image shows the T2 weighted MRE magnitude as geometric reference.

SWS maps reconstructed from k-MDEV at 30.03 Hz vibration frequency for a selected slice in the phantom. The excitation plate is visible on the right side. First row shows OMME results with one to four MEGs combined. The second row shows SWS recovered from Laplacian based unwrapped phase images with MEG of different strength. Last row shows SWS recovered from Flynn unwrapped phase images. Grayscale for SWS maps ranges from 0 to 1 m/s.

SWS maps for OMME (MEGs=4,8,16,32mT/m) and Laplace and Flynn unwrapping (MEG=32mT/m) at different slices. The anatomical reference from MRE magnitude is included (region of interest demarcated in red for noise estimation). Red arrows indicate where OMME shows greater contrast in the SWS map. A) Volunteer 1 for vibration frequency 25Hz at two different slices. Grayscale ranges from 0.3-1.8m/s. B) Volunteer 2 for vibration frequency 30Hz at two different slices. Grayscale ranges from 0.2-2.2 m/s.

Table 1: MRI sequence parameters for phantom and in vivo experiments.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1019