1014
Viscoelastic MRE Phantoms with Tunable Damping Ratio Independent of Shear Stiffness1Biomedical Engineering, University of Delaware, Newark, DE, United States, 2Thayer School of Engineering, Dartmouth College, Hanover, NH, United States
Synopsis
This study validates the use of LPAA/PAA gels as viscoelastic MRE phantoms with tunable damping ratio independent of shear stiffness. PAA concentration was 6wt% across all phantoms while LPAA concentration ranged from 0 to 6wt%. High-resolution MRE scans were conducted with 600, 700, 800, and 900 Hz vibrations. For each frequency, storage modulus and shear stiffness were constant while loss modulus and damping ratio increased with increasing LPAA concentration. For each LPAA concentration, loss modulus increased with increasing frequency indicating viscoelastic behavior. These results verify the independent tunability of damping ratio and shear stiffness.
Introduction
Physiologically accurate test samples, with known properties and characteristics, are essential for developing sensitive, repeatable, and accurate quantitative MRI techniques. Phantoms for magnetic resonance elastography (MRE) need to resemble tissue mechanical properties, specifically shear stiffness and damping ratio, as they reflect tissue microstructural composition and organization in vivo. Tunable shear stiffness materials are commonly used as MRE phantoms1,2, however, these materials do not often exhibit strong viscous properties and thus have very low damping ratios that are not tunable. Damping ratio is becoming an important MRE parameter for several applications, including cancer and memory function relationships3-5, but it remains more challenging to estimate than stiffness.6 Therefore, phantoms with independently tunable shear stiffness and damping ratio are important for developing and benchmarking the quantitative performance of MRE methods.One promising candidate is a viscoelastic gel made from linear polyacrylamide (LPAA) entrapped in a polyacrylamide (PAA) network, where viscosity is controlled by LPAA concentration. While the viscoelastic tunability of these gels was verified on the microscale, there has yet to be a study analyzing damping ratio, its tunability on larger gels, and its suitability for use in MRE phantoms.7 In this study, we evaluate the use of LPAA/PAA gels as physiologically accurate and tunable phantoms via high-resolution MRE.
Methods
Phantom PreparationLPAA/PAA phantoms (n = 4) were prepared in 50 mL conical tubes following a similar procedure as previously published.7 LPAA solution was created by polymerizing acrylamide, then mixed with acrylamide and bis-acrylamide as a cross-linking agent, then polymerized to create the LPAA/PAA gels. This process keeps the LPAA from crosslinking into the network that in turn introduces a viscous component to the material. The elastic component for all phantoms was a solution of 6wt% PAA, and the viscous component was varied across the phantoms between 0, 2, 4, and 6wt% LPAA. The final phantom volume was 25 mL.
MRE Imaging
To measure their mechanical properties, each of the four phantoms underwent a frequency sweep of MRE scans. All scans were conducted on a 9.4T Bruker BioSpec preclinical imaging system (Bruker Corporation, Billerica, MA). Vibrations were applied to the phantoms via a nonmagnetic, piezoelectric actuator (APA150M; Cedrat Technologies, Meylan, France) at 600, 700, 800, and 900 Hz. A custom MRE-EPI sequence was used in these experiments with motion encoding gradients applied in three directions, with four phase offsets and positive and negative gradient polarities to capture 3D wave motion. All scans were acquired using the following imaging parameters: TE/TR = 60/2000 ms, slices = 20, slice thickness = 0.5 mm, FOV = 32 x 32 mm2, matrix = 64 x 64, resolution = 0.5 mm isotropic.
Mechanical Property Estimation
The isotropic, nearly incompressible, nonlinear inversion algorithm (NLI) was used to estimate mechanical properties from MRE displacement data.6,8 NLI outputs storage modulus (G') and loss modulus (G'') which are the real and imaginary components of complex shear modulus (G = G' + G''). These parameters were then used to calculate shear stiffness $$$(µ = 2|G|^2/(G' + |G|))$$$ and damping ratio $$$(ξ = G''/(2G'))$$$.9,10 ROI-based analyses were conducted to assess the trends in G', G'', μ, and ξ with respect to LPAA concentration and actuation frequency.
Results & Discussion
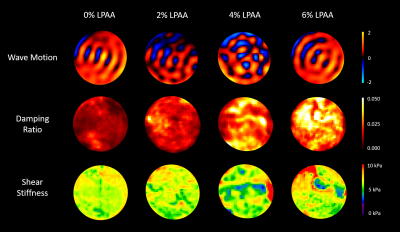
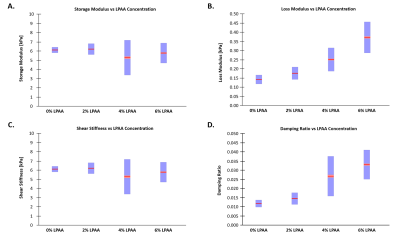
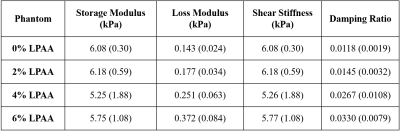
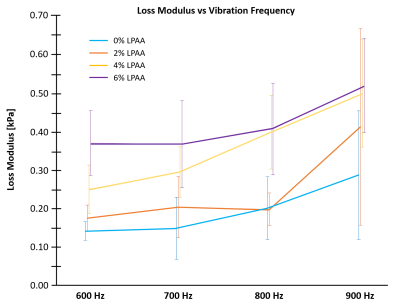
Figure 1 shows a representative slice for all four phantoms actuated at 600 Hz. For all phantoms, there was substantial wave motion and strong MR signal. While the shear stiffness remained relatively constant across the four phantoms, the damping ratio increased progressively with increasing LPAA concentration. Figure 2 quantifies these parameters with the damping ratio increasing from 0.012 for the 0wt% LPAA phantom to 0.033 for the 6wt% LPAA phantom. The storage modulus remained constant with LPAA concentration, similar to shear stiffness, while the loss modulus increased. Table 1 summarizes the observed values. These results suggest that the increases in loss modulus were responsible for increases in damping ratio, while the constant storage modulus was likely responsible for the consistency in shear stiffness. However, there was some heterogeneity in the property maps, especially in the 4wt% LPAA phantom, which may be attributed to imperfections during the gelling process. A larger sample size could help confirm these observations.From the frequency sweep, we observe a clear increase in loss modulus across the four actuation frequencies tested in all four phantoms (Figure 3). These results reflect the relationship between applied vibration and shear rate, which is intrinsic to viscoelastic materials. In future work, we will model these trends quantitatively using frequency dependence parameters such as the power law coefficient (α).11
Conclusion
From this preliminary study, we concluded that LPAA/PAA gels are suitable for use as MRE phantoms with tunable damping ratio independent of shear stiffness. We verified that LPAA/PAA gels have sufficient MR signal and that damping ratio could be tuned via changes in LPAA concentration without altering the shear stiffness. While the damping ratios measured were below the physiological range in brain tissue (0.1-0.4),12 these results suggest that larger damping ratios within this range could be achieved by further increasing the LPAA concentration. These gels may facilitate the creation of heterogeneous phantoms with damping ratio contrast that more accurately model soft tissue viscoelasticity.Acknowledgements
NIH grants R01-EB027577 and R01-AG058853 and the Delaware INBRE program P20-GM103446.References
1. McIlvain G, Ganji E, Cooper C, Killian ML, Ogunnaike BA, Johnson CL. Reliable Preparation of Agarose Phantoms for Use in Quantitative Magnetic Resonance Elastography. J Mech Behav Biomed Mater. 2019;97(Sep):65-73.
2. Kashif AS, Lotz TF, McGarry MD, Pattison AJ, Chase JG. Silicone Breast Phantoms for Elastographic Imaging Evaluation. Med Phys. 2013;40(6):063503.
3. Schwarb H, Johnson CL, McGarry MDJ, Cohen NJ. Medial temporal lobe viscoelasticity and relational memory performance. Neruoimage. 2016;132(May):534-541.
4. Yin M, Glaser KJ, Manduca A, et al. Distinguishing between hepatic inflammation and fibrosis with MR elastography. Radiology. 2017;284(3):694-705.
5. Balleyguier C, Lakhdar A Ben, Dunant A, Mathieu MC, Delaloge S, Sinkus R. Value of whole breast magnetic resonance elastography added to MRI for lesion characterization. NMR Biomed. 2018;31(1):1-10.
6. McGarry MDJ, Van Houten EEW, Johnson CL, Georgiadis JG, Sutton BP, Weaver JB, Paulsen KD. Multiresolution MR elastography using nonlinear inversion. Med Phys. 2012;39:6388–6396.
7. Charrier EE, Pogoda K, Wells RG, Janmey PA. Control of cell morphology and differentiation by substrates with independently tunable elasticity and viscous dissipation. Nat Commun. 2018;9(1):1-13.
8. Van Houten EEW, Miga MI, Weaver JB, Kennedy FE, Paulsen KD. Three-dimensional subzone-based reconstruction algorithm for MR elastography. Magn Reson Med. 2001;45(5):827-837.
9. Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, et al. Magnetic Resonance Elastography: Non-invasive Mapping of Tissue Elasticity. Med Image Anal. 2001;5(4):237-254.
10. McGarry MDJ and Van Houten EEW. Use of a Rayleigh damping model in elastography. Med Biol Eng Comput. 2008;46(8):759-766.
11. Testu J, McGarry MDJ, Dittmann F, et al. Viscoelastic power law parameters of in vivo human brain estimated by MR elastography. J Mech Behav Biomed Mater. 2017;74(April):333-341.
12. Hiscox LV, McGarry MDJ, Schwarb H, et al. Standard-space atlas of the viscoelastic properties of the human brain. Hum Brain Mapp. 2020;41(18):5282-5300.
Figures