1013
MR Elastography Reconstruction Based on a Linear Integral Equation Derived from the Helmholtz Identity
Motofumi Fushimi1, Naohiro Eda1, and Takaaki Nara1
1The University of Tokyo, Tokyo, Japan
1The University of Tokyo, Tokyo, Japan
Synopsis
This paper presents a novel reconstruction method for MR Elastography. Unlike most conventional methods that solve Navier's partial differential equation (PDE), the proposed approach solves a linear integral equation derived from Helmholtz’s identity. The proposed method can reconstruct the complex shear modulus without calculating higher-order derivatives of the measured displacement data, nor solving a nonlinear minimization problem that could result in local minima. Our preliminary study by numerical simulations demonstrated that the proposed method could robustly estimate the complex shear modulus. Future work is to compare the effectiveness of the proposed method with the PDE-based conventional methods.
Introduction
The core part of MR elastography (MRE) involves reconstructing the complex shear modulus from displacement field data1,2. Most of the conventional MRE reconstruction methods are based on Navier's partial differential equation (PDE), which directly relates the elastic moduli $$$λ$$$ and $$$μ$$$ to the displacement field $$$\boldsymbol{u}$$$. The AIDE method3 ignores the spatial variations of the elastic moduli in Navier's PDE to derive a simple algebraic reconstruction formula, resulting in severe artifacts in boundary regions of different tissues. To overcome this, several methods have been proposed. The direct methods4,5 solving the PDE for $$$μ$$$ are sensitive to noise due to numerical calculation of higher-order differentials of $$$\boldsymbol{u}$$$. On the other hand, the iterative methods6,7 perform a nonlinear minimization of the difference between the measured and calculated $$$\boldsymbol{u}$$$ from a given $$$μ$$$, possibly resulting in local minima. In this paper, we propose a novel MRE reconstruction method that solves a linear integral equation (IE) of $$$μ$$$ and the other Lame's parameter $$$λ$$$ derived from Helmholtz's identity for the stress tensor fields. The proposed method estimates $$$μ$$$ without calculating higher-order derivatives of the measured data, nor iteratively updating the estimate.Method
The time-harmonic displacement field $$$\boldsymbol{u}$$$ measured in MRE and the stress field $$$\boldsymbol{σ}$$$ are governed by the following equation of motion (1) and Hooke's law (2): $$\nabla\cdot\boldsymbol{σ}=-ρ_{0}ω_{0}^{2}\boldsymbol{u},\tag{1}$$ $$\boldsymbol{σ}=λ\nabla\cdot\boldsymbol{u}\boldsymbol{I}+μ\check{\nabla}\boldsymbol{u},\tag{2}$$ where $$$ω_{0}$$$ is the frequency of the external mechanical excitation, $$$ρ_{0}$$$ is the mass density of water, and $$$\check{\nabla}\boldsymbol{f}\equiv\nabla\boldsymbol{f}+\nabla\boldsymbol{f}^{\top}$$$. In the conventional methods, $$$\boldsymbol{σ}$$$ is eliminated from Eqs. (1) and (2) to derive Navier's PDE that directly relates the measured data to the elastic moduli. We derive a linear IE of $$$λ$$$ and $$$μ$$$ based on Helmholtz's identity for the stress tensor fields by exploiting the fact that Eq. (1) constraints its divergence.As discussed in [8], Helmholtz's identity also holds for tensor fields. A smooth tensor field $$$\boldsymbol{f}$$$ defined in a bounded region of interest (ROI) $$$Ω$$$ can be represented by its divergence and curl as follows: $$\boldsymbol{f}(\boldsymbol{r})=-\oint_{{\partial}Ω}{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r})(\boldsymbol{n}\cdot\boldsymbol{f})\mathrm{d}S^{\prime}+\int_{Ω}{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r})(\nabla\cdot\boldsymbol{f})\mathrm{d}V^{\prime}+\oint_{{\partial}Ω}{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r})(\boldsymbol{n}\times\boldsymbol{f})\mathrm{d}S^{\prime}-\int_{Ω}{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r})\times(\nabla\times\boldsymbol{f})\mathrm{d} V^{\prime},\tag{3}$$ where $$$G(\boldsymbol{r}^{\prime};\boldsymbol{r})=1/(4π\lvert\boldsymbol{r}^{\prime}-\boldsymbol{r}\rvert)$$$. By applying integration by parts to the last term of Eq. (3), we obtain $$\boldsymbol{f}(\boldsymbol{r})=-\oint_{{\partial}Ω}{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r})(\boldsymbol{n}\cdot\boldsymbol{f})\mathrm{d}S^{\prime}+\int_{Ω}{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r})(\nabla \cdot \boldsymbol{f})\mathrm{d}V^{\prime}+\int_{Ω}((\boldsymbol{f}^{\top}\times\nabla)\times{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r}))^{\top}\mathrm{d}V^{\prime},\tag{4}$$ which represents a tensor field using its divergence and itself instead of its curl. Now, let us consider Helmholtz's identity for the stress tensor. Letting $$$\boldsymbol{f}$$$ in Eq. (4) be $$$\boldsymbol{σ}$$$ and substituting Eqs. (1) and (2) into Eq. (4) yields $$λ\nabla\cdot\boldsymbol{u}\boldsymbol{I}+μ\check{\nabla}\boldsymbol{u}=-\oint_{{\partial}Ω}{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r})(\boldsymbol{n}\cdot(λ\nabla\cdot\boldsymbol{u}\boldsymbol{I}+μ\check{\nabla}\boldsymbol{u}))\mathrm{d}S^{\prime}-\int_{Ω}{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r})ρ_{0}ω_{0}^{2}\boldsymbol{u}\mathrm{d}V^{\prime}+\int_{Ω}(((λ\nabla\cdot\boldsymbol{u}\boldsymbol{I}+μ\check{\nabla}\boldsymbol{u})^{\top}\times\nabla)\times{\nabla}G(\boldsymbol{r}^{\prime};\boldsymbol{r}))^{\top}\mathrm{d}V^{\prime}.\tag{5}$$ Given the elastic moduli values on $$${\partial}Ω$$$, the surface integrals can be calculated. Then, Eq. (5) is a linear IE for $$$λ$$$ and $$$μ$$$ including only first-order derivatives of $$$\boldsymbol{u}$$$, which can be calculated using the Savitzky-Golay filter9 and efficiently solved by the FFT-CG method10.
We tested the proposed method by numerical simulations and compared the results with the incompressible-AIDE method3. The simulation was performed using FEM software COMSOL Multiphysics 5.5 (COMSOL Inc.). We constructed a cylinder and a sphere model for the simulations as shown in Fig. 1. An external force oscillating at $$$ω_{0}=2π\times30~\mathrm{Hz}$$$ and oriented in the $$$y$$$-direction was applied to the red plane and the displacement field was obtained on eight slices (the blue planes) with a resolution of $$$1.4\times1.4\times5~\mathrm{mm^{3}}$$$. The fixed boundary condition was set on the green plane.
Results and Discussion
Figure 2 shows the reconstructed storage and loss moduli maps of the cylinder model when no noise was added. The results of the incompressible-AIDE method contain severe artifacts at the boundary of the background region and the inclusion due to the local homogeneity assumption. The values of the inclusion are further distorted because the incompressible assumption $$$\nabla\cdot\boldsymbol{u}=0$$$ is violated. In contrast, the proposed method gives accurate and stable results for both shear modulus and viscosity since it does not depend on local homogeneity or incompressibility assumptions. The proposed method has the lower L2 error as shown in the table. The error of shear viscosity is higher than that of shear modulus. This is because $$$\mathrm{Re}[μ]>\mathrm{Im}[μ]$$$ holds at the simulated frequency and the shear modulus contributes more to the displacement. Thus, using a higher frequency could improve shear viscosity estimation, but at the cost of attenuating the shear wave.Figure 3 shows the reconstruction results of the same model when 1% Gaussian noise was added. Using the incompressible-AIDE method, the resulting images are noisy due to the numerical calculation of higher-order derivatives of the measured data. The proposed method yields better results and total variation (TV) regularization further stabilize reconstruction while preserving contrast.
Figure 4 shows the reconstruction results of the sphere model. The proposed method is shown to be feasible for reconstructing three-dimensional objects.
Conclusion
We proposed a novel MRE reconstruction method that solves a linear IE of shear modulus derived from Helmholtz's identity for tensor fields. This method can reconstruct the shear modulus directly without calculating higher-order derivatives of the measured data. Our preliminary study by numerical simulations demonstrated that the proposed method could estimate the shear modulus more stably than the incompressible-AIDE method. Future work is to compare the proposed method with other conventional methods based on Navier's PDE.Acknowledgements
This work was financially supported by Canon Medical Systems Corporation.References
- H. Dong, R. D. White, and A. Kolipaka, "Advances and Future Direction of Magnetic Resonance Elastography," Topics Magn. Reson. Imag., 27(5):363-384, 2018.
- D. Fovargue, S. Kozerke, R. Sinkus, and D. Nordsletten, "Robust MR elastography stiffness quantification using a localized divergence free finite element reconstruction," Med. Imag. Anal., 44:126--142, 2018.
- T. E. Oliphant, A. Manduca, R. L. Ehman, and J. F. Greenleaf, "Complex-valued stiffness reconstruction for magnetic resonance elastography by algebraic inversion of the differential equation," Magn. Reson. Med., 45(2):299--310, 2001.
- M. Honarvar, R. Sahebjavaher, R. Sinkus, R. Rohling, and S. E. Salcudean, "Curl-Based Finite Element Reconstruction of the Shear Modulus Without Assuming Local Homogeneity: Time Harmonic Case," IEEE Trans. Med. Imag., 32(12):2189--2199, 2013.
- M. Honarvar, R. Rohling, and S. E.Salcudean, "A comparison of direct and iterative finite element inversion techniques in dynamic elastography," Phys. Med. Biol., 61(8):3026--3048, 2016.
- E. E. W. Van Houten, M. I. Miga, J. B. Weaver, F. E. Kennedy, and K. D. Paulsen, "Three-dimensional subzone-based reconstruction algorithm for MR elastography," Magn. Reson. Med., 45(5):827--837, 2001.
- A. A. Oberai, N. H. Gokhale, and G. R. Feijóo, "Solution of inverse problems in elasticity imaging using the adjoint method," Inv. Probl., 19(2):297--313, 2003.
- T. McGraw, T. Kawai, I. Yassine, and L. Zhu, "Visualizing High-Order SymmetricTensor Field Structure with Differential Operators," J. App. Math., 2011(142923):1-27, 2011.
- A. Savitzky, and M. J. E. Golay, "Smoothing and Differentiation of Data by Simplified Least Squares Procedures," Anal. Chem., 36(8):1627-1639, 1964.
- M. F. Cátedra, J. G. Cuevas, and L. Nuno, "A scheme to analyze conducting plates of resonant size using the conjugate-gradient method and the fast Fourier transform," IEEE Trans. Antennas Propag., 36(12):1744-1752, 1988.
Figures
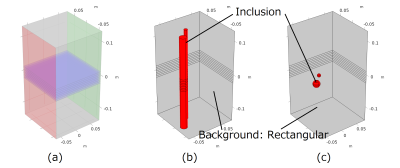
Figure1: (a) The simulation system (red: excitation plane, green: fixed surface, blue: measurement planes), (b) the cylinder model, and (c) the sphere model used in the numerical simulations. Inclusions in red color have different elastic moduli from those of the background.
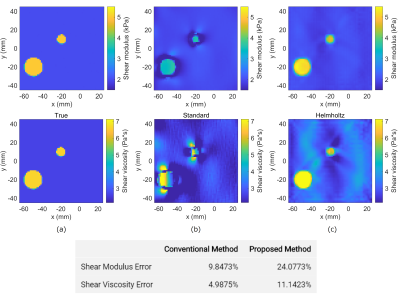
Figure 2: Shear modulus and viscosity maps for the cylinder model when no noise is added. (a) The true maps, (b) the reconstruction results of the conventional method, and (c) the reconstruction results of the proposed method. The table at the bottom shows the normalized L2 errors associated with each method.
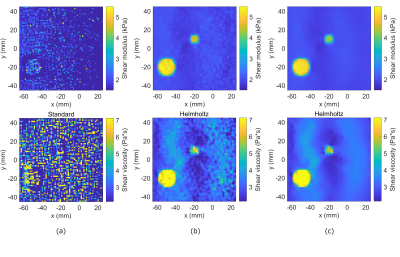
Figure 3: Shear modulus and viscosity maps for the cylinder model when 1% Gaussian noise is added. The reconstruction results of (a) the conventional method, (b) the proposed method with no regularization, and (c) the proposed method with TV regularization.
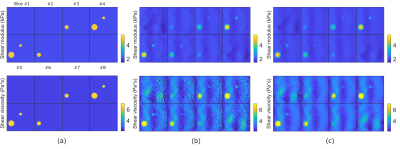
Figure 4: Shear modulus and viscosity maps for the sphere model when 1% Gaussian noise is added. Each figure shows results for all eight slices. (a) The true maps, (b) the reconstruction results of the proposed method with no regularization and (c) the reconstruction results of the proposed method with TV regularization.