1012
A Learned Phase Correction Algorithm Outperforms a Conventional Filter for 3D Vector MRE
Jonathan M Trevathan1, Jonathan M Scott1, Joshua D Trzasko1, Armando Manduca1, John Huston1, Richard L Ehman1, and Matthew C Murphy1
1Mayo Clinic, Rochester, MN, United States
1Mayo Clinic, Rochester, MN, United States
Synopsis
Bulk motion during the motion encoding of multi-slice spin-echo EPI pulse sequences used to acquire 3D MRE data creates a slice-to-slice phase jitter. A 3D convolutional neural network was trained to estimate a phasor corresponding to noise-free displacements given noisy, complex-valued MRE data. The net outperformed its filtering counterpart in noisy and noise-free simulation data, and decreased test-retest repeatability error in vivo.
Introduction
Full 3D wavefield magnetic resonance elastography (MRE) data are usually acquired with multi-slice spin-echo planar sequences. Bulk motion during the motion encoding causes spurious phase jitter from slice to slice. The curl calculation that is often used to remove the effects of longitudinal waves amplifies untreated jitter. Currently, phase jitter is reduced using in-plane filtering techniques that either subtract away slowly varying in-plane phase,1 or subtract a constant phase from each slice to minimize second-order differences in phase across slices.2 Our experience is with the former method, referred to here as low-pass subtraction (LPS). We observe that artifact is incompletely mitigated in some cases, causing errors in stiffness images generated by 3D inversion processing. We hypothesized that higher performance would be achieved by a neural network trained to recognize and remove slice-to-slice phase discontinuities, while simultaneously denoising the data.Method
Algorithm trainingAn Inception-like convolutional network was trained to learn a phasor corresponding only to the shear displacements. Training data were complex-valued image patches generated according to a prescribed forward model. For each training example, the magnitude was taken from in vivo brain MRE data while the phase was prescribed by 6 components:
- Simulated shear wave field (u) computed using an analytical wave equation (maximum stiffness of 5 kPa, maximum damping ratio of 0.6)
- Simulated background phase field (3rd order 3D polynomial) modeling the composite effects of B0 inhomogeneity, eddy currents, and concomitant fields
- Slice-to-slice perturbation (max of 25%) of the background phase
- Linear phase ramp (max range of ±70 radians) in the slice direction
- Slice-to-slice perturbation of the linear phase ramp (corresponding to motion up to 3 mm)
- Random constant (0-2π) to shift the location of phase wrapping.
Simulation experiment
A simulated data set was generated to test the algorithm against known displacements. Displacements were computed using a finite difference model (FDM) of the governing equation for linear, elastic, isotropic materials with brain geometry derived from the T1-weighted image of a 55-year-old healthy male volunteer.3 Brain voxels were assigned a stiffness of 2 kPa and a damping ratio of 0.25; cerebrospinal fluid (CSF) voxels were assigned 0.15 kPa stiffness and 0.7 damping ratio. Using Dirichlet boundary conditions, a 60-Hz harmonic bulk displacement in the anterior-posterior direction was applied to CSF voxels, excluding the ventricular system, and the FDM was solved using 20,000 iterations of the conjugate gradient method. The forward model described above was applied to create a simulated MRE data set with known displacements. The SNR (10-50) and background phase field (3rd polynomial, max of 0-2pi) were random for each motion direction and time offset. A second simulated data set without i.i.d. noise was generated in the same manner to separate the effects of artifact removal and denoising. Displacement images were computed in three ways:
- Phase subtraction of positive and negative encoding directions → phase unwrapping4 → temporal Fourier transform
- LPS → phase subtraction of encoding directions → phase unwrapping → temporal Fourier transform
- Net denoising → phase unwrapping → temporal Fourier transform
In vivo experiment
This experiment used previously acquired data from a brain MRE repeatability study in which 10 volunteers were scanned 3 times each.5 First, displacement images were computed in three ways, as in the simulation experiment. The curl was then computed with a neural network trained to perform numerical differentiation, and stiffness maps were computed by neural network inversion.6 For each filtering method, repeatability of global brain stiffness was summarized as the coefficient of variation (CV) in each volunteer. Differences in CV between filtering methods were tested with a linear mixed-effects model (P<0.05 significant).
Results
Correlation coefficients of the first harmonics of the displacements (Fig 1&2) were calculated and plotted for each of the processing methods: no filter, LPS filter, and neural net denoising. This was done for both the noisy and noise-free simulated data. Example in vivo curl images are shown in Fig 3. Both filtering methods significantly reduced CVs relative to no filtering, but the two filters did not have significantly different CVs (Fig 4).Conclusion
The neural net-based phase correction best reproduced the true displacement values in simulation (Fig 1&2). The improvement in performance for both noisy and noise-free data suggests the higher correlation given by the net is due to improved slice to slice dejittering. In vivo, the net further reduces jitter artifact relative to LPS (Fig 3). Moreover, an examination of the CV in the repeatability study shows that the net reduces CV relative to LPS, though not to a statistically significant degree in this sample.Acknowledgements
This work was supported by NIH grants EB001981 and EB027064.References
- Murphy, M. C., Huston 3rd, J., Glaser, K., Manduca, A. & Felmlee, J. Phase correction for interslice discontinuities in multislice EPI MR elastography. Montreal, 3426 (2012).
- Barnhill, E. et al. Fast Robust Dejitter and Interslice Discontinuity Removal in MRI Phase Acquisitions: Application to Magnetic Resonance Elastography. IEEE Trans Med Imaging 38, 1578-1587, doi:10.1109/TMI.2019.2893369 (2019).
- Arani, A. et al. Measuring the effects of aging and sex on regional brain stiffness with MR elastography in healthy older adults. Neuroimage 111, 59-64, doi:10.1016/j.neuroimage.2015.02.016 (2015).
- Bioucas-Dias, J. M. & Valadao, G. Phase unwrapping via graph cuts. IEEE Trans Image Process 16, 698-709 (2007).
- Murphy, M. C. et al. Measuring the characteristic topography of brain stiffness with magnetic resonance elastography. PLoS One 8, e81668, doi:10.1371/journal.pone.0081668 (2013).
- Murphy, M. C. et al. Artificial neural networks for numerical differentiation with application to magnetic resonance elastography in Proceedings of the ISMRM (2020).
Figures

Simulated data with noise. Top) Left: Correlation with no filter.
Middle: Correlation with LPS filter. Right: Correlation with neural net
denoising. Bottom) from left to right: Original displacements, no filter, LPS filter,
neural net denoising.
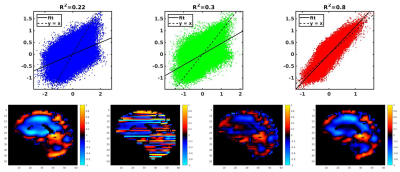
Simulated data without noise. Top) Left:
Correlation with no filter. Middle: Correlation with LPS filter. Right:
Correlation with neural net denoising. Bottom) from left to right: Original
displacements, no filter, LPS filter, neural net denoising.

Sagittal view of calculated x component
of the curl from in vivo data. Left: No Filter. Middle: LPS filter. Right:
Neural net denoised.
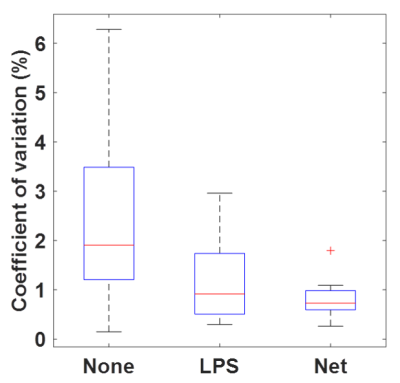
Coefficient of variation for no filter, low-pass
subtraction (LPS) filter, and neural net denoiser for in-vivo data.