0917

RF-encoding for improved multi-voxel separation in MR spectroscopy

Adam Berrington¹, Penny Gowland¹, and Richard Bowtell¹
¹Sir Peter Mansfield Imaging Centre, School of Physics and Astronomy, University of Nottingham, Nottingham, United Kingdom

Synopsis

The simultaneous acquisition and separation of signals from multiple voxels using receive sensitivities can accelerate MRS acquisition. However, separation is ill-conditioned when signals are acquired from voxels with similar receive-coil sensitivities. We propose a new approach which improves reconstruction using the transmitted RF to modulate the signals from different voxels. Simulations showed that for a small number of encoding steps, M, the g-factor of the reconstruction problem was reduced (~3-fold, M=2 for 5 regions). Reconstructed phantom data from two-voxels, acquired using phase-modulation, were of higher SNR than coil-encoding, indicating the potential of the proposed method for multi-voxel measurement in MRS.

Introduction

Multi-voxel acquisition allows for acceleration of MRS by simultaneously acquiring signals from several regions. The separation of resulting signals using receive-coil sensitivities¹ has been demonstrated for two voxel MRS^2,3. However, its application is challenging in regions where sensitivity profiles are similar, leading to high g-factors, and this prevents extension to multiple- or closely spaced voxels. In simultaneous multi-slice imaging, shifting of the transmitted RF phase can lower g-factors for higher accelerations⁴. A framework for selective excitation to encode signals has been suggested in MRI^5,6. Thus, we propose signal modulations, using the transmitted RF, to improve the conditioning of reconstruction for multi-voxel MRS, and provide an initial demonstration of this approach at 7 T.

Theory

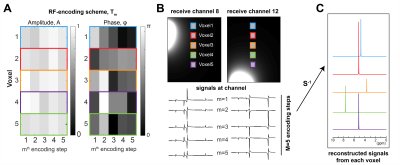
The proposed method generalises multi-voxel excitation by modulating the signal in each desired voxel, $$$n$$$, by a complex weighting, $$$T_{m}$$$, using the applied RF pulse. For a multichannel receive-coil, the measured signal $$$C_{l,m}$$$ in the $$$l^{th}$$$ coil arising from $$$N$$$ discretised regions can thus be written,

$$C_{l,m} = \sum_{n=1}^N x(n)r_{l}(n)T_{m}(n)$$

where the desired signals, $$$x$$$, are weighted by the coil’s receive sensitivity at the voxel location, $$$r_{l}$$$. If acquisition is repeated over $$$M$$$ encoding steps, the signal equation can be concatenated into matrix form such that,

$$\bf C = Sx$$

where $$$\bf S$$$ is the system matrix, which can be inverted⁵ to determine the signals from each region, $$$\bf x$$$. As in SENSE coil-encoding, effective geometry factors, g, are calculated from $$$\bf S$$$ to quantify the signal-to-noise (SNR) penalty of unfolding^1,2, where

$$g = \sqrt{(\bf{S}^{H}S)^{-1}(S^{H}S)}$$

assuming receiver noise covariance is equal to unity.

Methods

Simulations of the proposed method were performed on 5 voxels (20x20mm²) using a 2D computational phantom⁷ with 16 receive channels (256x256mm²). At each voxel position, a signal was modelled by a complex exponential decay at a single frequency (0.1, 0.5, -1, 0.5, 3) ppm for voxels 1 to 5 with variable amplitude. To simulate RF-encoding, the signal phase and amplitude within each voxel were modulated over M steps according to the encoding scheme shown in Fig. 1A and the signals received by different channels were evaluated. Noise covariance was set to unity. Experiments were repeated with M=1…5, where M=1 corresponds to pure coil-encoding. The SNR penalty was calculated as the maximum g-factor divided by the mean amplitude modulation over all encoding steps.

To verify the approach experimentally, dual-band RF waveforms were generated by frequency-shifting an asymmetric single-band pulse (max. B₁=9 μT, dur=4.4 ms) [8] using a time-dependent phase modulation, and then summing this with the original single-band pulse. A total of 5 RF-modulated pulses were generated by introducing an incremental static phase, $$$\phi_m$$$, on the frequency-shifted band, such that $$$\phi_m = 30^{\circ}(m-1)$$$ with $$$m=1...5$$$.

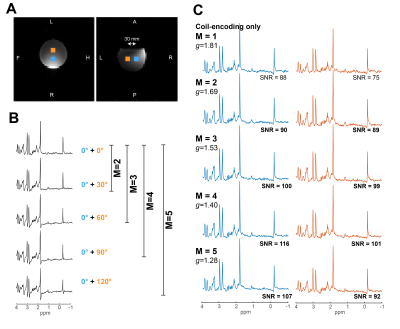
MR scanning was performed on a Philips 7 T Achieva MR system with 32-channel receive-array head coil. MRS data from two voxels (15x15x15cm³) were acquired in a homogeneous phantom containing standard brain metabolites using semi-LASER (TE/TR=31ms/3s, NT=64). The excitation pulse was switched each TR using the dual-band pulses according the encoding scheme. A total of 5 experiments were performed, each with a different number of encoding steps, M=1…5 (M=1 corresponds to pure coil-encoding). No phase cycling was performed. Sensitivity maps were obtained using a 2D-GRE sequence normalised to data recorded using the volume coil for receive. Spectral SNR (peak NAA height over noise -5 to -2 ppm) and maximum g-factors were calculated and compared to coil-encoding alone.

Results

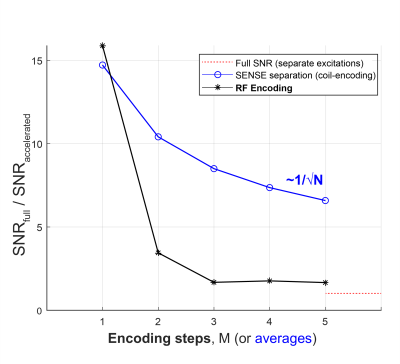
Fig. 1 shows simulated spectra from 5 regions reconstructed using amplitude and phase-weighted RF-encoding (Fig. 1). As expected, the maximum g-factor was high for the 5 adjacent voxels g=14.72, limiting source separation without RF-encoding (Fig. 2). However, there was a considerable theoretical SNR improvement after including only M=2 encoding steps (g=3.44, ~3-fold vs. coil-encoding) with the increase in SNR plateauing from M=3 to M=5.

The dual-band RF pulses were observed to impart phase modulation in the second band (Fig. 3). Pulses were 4.4 ms duration (max. B₁=17 μT) with 1.5 kHz bandwidth. Data from the phantom revealed good separation of two voxels using RF-encoding (M=2 to 5), yielding spectra of high quality from both regions (Fig. 4). The g-factor decreased from 1.81 (coil-encoding only, M=1) to 1.28 (RF-encoding, M=5). The spectral SNR increased with M (apart from M=5) and was higher than that produced using coil-encoding alone with the same number of averages.

Discussion & Conclusion

We have proposed a method to improve the separation of multi-voxel MRS data using modulation of the signal in each region with RF excitation. Signals reconstructed from 5 voxels in simulation had lower g-factor penalties compared to coil-encoding through improved conditioning of signal unfolding, even after only 2 RF-encoding steps. Phantom data from two voxels were separated with higher SNR compared to coil-encoding alone, using small phase modulations (30º) and a small number of encoding steps M≤5. This method may be optimised; for instance, RF-encoding schemes may be tailored to complement measured sensitivity profiles. Since multiple averages are commonly acquired in MRS, the encoded approach requires no increase in scan time. Further work, however, is needed to investigate suitable high-bandwidth low-power pulses suitable for RF-encoding⁹. Future work will explore the approach with more voxels in vivo and in inhomogeneous phantoms.

Acknowledgements

The authors would like to thank the support of the Precision Imaging Beacon, University of Nottingham.

References

¹ K. P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger, “SENSE: sensitivity encoding for fast MRI.,” Magn. Reson. Med., vol. 42, no. 5, pp. 952–62, Nov. 1999.

² V. O. Boer, D. W. J. Klomp, J. Laterra, and P. B. Barker, “Parallel reconstruction in accelerated multivoxel MR spectroscopy,” Magn. Reson. Med., vol. 74, no. 3, pp. 599–606, Sep. 2015.

³ G. Oeltzschner, N. A. J. Puts, K. L. Chan, V. O. Boer, P. B. Barker, and R. A. E. Edden, “Dual-volume excitation and parallel reconstruction for J-difference-edited MR spectroscopy,” Magn. Reson. Med., vol. 77, no. 1, pp. 16–22, 2017.

⁴ F. A. Breuer, M. Blaimer, R. M. Heidemann, M. F. Mueller, M. A. Griswold, and P. M. Jakob, “Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging,” Magn. Reson. Med., vol. 53, no. 3, pp. 684–691, Mar. 2005.

⁵ W. E. Kyriakos, W. S. Hoge, and D. Mitsouras, “Generalized encoding through the use of selective excitation in accelerated parallel MRI,” NMR Biomed., vol. 19, no. 3, pp. 379–392, 2006.

⁶ W. E. Kyriakos et al., “Sensitivity profiles from an array of coils for encoding and reconstruction in parallel (SPACE RIP),” Magn. Reson. Med., vol. 44, no. 2, pp. 301–308, 2000.

⁷ Guerquin-Kern, M., Lejeune, L., Pruessmann, K. P. & Unser, M. Realistic Analytical Phantoms for Parallel Magnetic Resonance Imaging. IEEE Trans. Med. Imaging 31, 626–636 (2012).

⁸ Z. Starcuk, K. Bartusek, and Z. Starcuk, “Asymmetric Amplitude-Modulated Radiofrequency Pulses and Their Application to Band-Selective Decoupling,” J. Magn. Reson. Ser. A, vol. 104, no. 3, pp. 340–344, Oct. 1993.

⁹ M. Barth, F. Breuer, P. J. Koopmans, D. G. Norris, and B. A. Poser, “Simultaneous multislice (SMS) imaging techniques,” Magn. Reson. Med., vol. 75, no. 1, pp. 63–81, 2016.

Figures

Fig.1: RF-encoding simulated with unique spectral peaks assigned to 5 voxel ‘locations’ (coloured regions). A) Encoding scheme applied to each voxel at each encoding step, $$$m=1…5$$$. Amplitude was weighted randomly between 0.8 and 1 and phase modulated between 0 and 180$$$^{\circ}$$$. B) Receive sensitivities (shown for two coils), which are combined with (A) to generate weighted signals at each channel for each encoding step, $$$m$$$. Signals are concatenated over M=5 steps. C) Inversion of the system matrix, $$$\bf S$$$, reveals reconstructed signals from each voxel.

Fig. 2: Simulated SNR penalty defined as the ratio of full SNR following separate excitations ($$$SNR_{full}$$$) compared to the accelerated cases ($$$SNR_{accelerated}$$$) for the 5 voxel acquisition. Encoding was increased from M=1 (coil-encoding only with m=1) to M=5. Since coil-encoding is performed without encoding steps, the SNR penalty is weighted by the number of additional averages acquired, $$$\sqrt{N}$$$, for comparison. For the encoded case, the SNR penalty is equal to the maximum g-factor divided by the mean amplitude modulation accounting for signal loss.

Fig 3: Dual-band pulses for RF encoding designed to excited two voxels 30 mm apart by complex modulation of an existing single band pulse. Pulse waveforms (left) and transverse magnetisation (right) are shown. The phase of the second band was manipulated in 30° increments to generate a series of m=1…5 dual-band excitation pulses for RF-encoding for use during scanning. The slice rephasing gradient is not simulated.

Fig. 4: Data acquired from two voxels (voxel 1=blue; voxel 2=orange) in a phantom (A) using proposed RF-encoded technique with an increasing number of encoding steps, M. (B) Combined signal (not unfolded) from all receive coils shows shot-to-shot variation in phase from (0°,30°,60°,90°,120°) modulation on voxel 2 using the dual-band pulses. (C) Reconstructed data using RF-encoding (steps M=2-5) are shown below coil-encoding only (M=1). The spectral SNR and effective g-factor values are stated next to each encoding.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0917