0913
Efficient NUFFT Backpropagation for Stochastic Sampling Optimization in MRI1Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States, 2Electrical Engineering and Computer Science, University of Michigan, Ann Arbor, MI, United States
Synopsis
Optimization-based k-space sampling pattern design often involves the Jacobian matrix of non-uniform fast Fourier transform (NUFFT) operations. Previous works relying on auto-differentiation can be time-consuming and less accurate. This work proposes an approximation method using the relationship between exact non-uniform DFT (NDFT) and NUFFT, demonstrating improved results for the sampling pattern optimization problem.
Introduction
There is growing interest in learning k-space sampling patterns for MRI using stochastic gradient descent optimization approaches [1-3]. For non-Cartesian sampling patterns, reconstruction methods typically involve non-uniform FFT (NUFFT) operations [4]. A typical FFT method involves frequency domain interpolation using Kaiser-Bessel kernel values that are retrieved by nearest-neighbor look-up in a finely tabulated kernel [5]. That look-up operation is not differentiable w.r.t. the sampling pattern, complicating auto-differentiation routines for back-propagation (gradient descent) for sampling pattern optimization. This paper describes an efficient and accurate approach for computing approximate gradients with respect to the sampling pattern for learning k-space sampling patterns.Methods
Here we consider the MRI measurement model: $$$\boldsymbol{y}=\boldsymbol{A}(\boldsymbol{\omega}) \boldsymbol{x}+\boldsymbol{\varepsilon}$$$, where $$$\boldsymbol{y} \in \mathbb{C}^{M}$$$ is the acquired data, $$$\boldsymbol{x} \in \mathbb{C}^{N}$$$ is the image. System matrix $$$\boldsymbol{A}=\boldsymbol{A}(\boldsymbol{\omega}) \in \mathbb{C}^{M \times N}$$$ has entries $$$a_{i j}=\mathrm{e}^{-\imath \vec{\omega}_{i} \cdot \vec{r}_{j}}$$$ for $$$\vec{\omega}_{i} \in \mathbb{R}^{D}$$$ and $$$\vec{r}_{j} \in \mathbb{R}^{D}$$$ where $$$D \in\{1,2,3, ...\}$$$ denotes the image dimensions. $$$\boldsymbol{\omega}=\left[\boldsymbol{\omega}^{[1]} \ \boldsymbol{\omega}^{[2]} \ \ldots \boldsymbol{\omega}^{[D]}\right]$$$ is the $$$M \times d$$$ vector representation of the non-Cartesian sampling pattern. Usually $$$\boldsymbol{A}$$$ is approximated by a NUFFT [4]. In the current setting, field inhomogeneity is not considered.With recent advances of auto-differentiation software such as TensorFlow and PyTorch, stochastic gradient descent has found wide application in the MRI community, including training reconstruction networks, optimization of RF pulses [6] and sampling patterns [1-3].
For sampling pattern optimization problem, usually the loss function has the following form, considering a single training example (or mini-batch) for simplicity:
$$L(\boldsymbol{\omega}) = \left\|f_{\boldsymbol{\theta}}(\boldsymbol{A}(\boldsymbol{\omega}) \boldsymbol{x})-\boldsymbol{x}\right\|,$$ where $$$f_{\boldsymbol{\theta}}(\cdot)$$$ corresponds to a differentiable reconstruction algorithm with parameters $$$\theta$$$ and $$$\boldsymbol{x}$$$ is the ground truth image. The update w.r.t loss function $$$L(\boldsymbol{\omega})$$$ usually involves gradients w.r.t. NUFFT operations. Previous methods [3] use the chain-rule and auto-differentiation, which can be potentially slow and inaccurate because of the interpolation operation. Here we investigate a different approach where we analyze on paper the gradient using the exact (slow) Fourier transform expression (NDFT) and then implement that gradient expression using NUFFT approximations.
Forward operator: For $$$\boldsymbol{x}$$$, $$$\frac{\partial \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{x}}=\boldsymbol{A}$$$ because $$$\boldsymbol{A} $$$ is a linear operator. For the $$$d$$$th column of $$$\boldsymbol{\omega} $$$, $$\left[\frac{\partial \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{\omega}^{[d]}}\right]_{i l} =\frac{\partial[\boldsymbol{A} \boldsymbol{x}]_{i}}{\partial \omega_{l}^{[d]}} =\frac{\partial}{\partial \omega_{l}^{[d]}} \sum_{j=1}^{N} \mathrm{e}^{-\imath \vec{\omega}_{i} \cdot \vec{r}_{j}} x_{j} =\left\{\begin{array}{ll}-\imath \sum_{j=1}^{N} \mathrm{e}^{-\imath \vec{\omega}_{i} \cdot \vec{r}_{j}} x_{j} r_{j}^{[d]}, & i=l \\0, & \text { otherwise. }\end{array}\right.$$ The summation is equal to the product of the $$$i$$$th row of $$$\boldsymbol{A}$$$ with $$$\boldsymbol{x} \odot \boldsymbol{r}^{[d]}$$$. Thus, the $$$M \times M$$$ Jacobian for the partial derivative of $$$\boldsymbol{A} \boldsymbol{x}$$$ w.r.t. $$$\boldsymbol{\omega}^{[d]}$$$ is $$$\frac{\partial \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{\omega}^{[d]}}=-\imath \operatorname{diag}\left\{\boldsymbol{A}(\boldsymbol{\omega})\left(\boldsymbol{x} \odot \boldsymbol{r}^{[d]}\right)\right\}$$$. For efficient computation, we approximate $$$\boldsymbol{A}$$$ by a NUFFT operator, and the Jacobian calculation is accomplished by simply applying the NUFFT operation to $$$\boldsymbol{x} \odot \boldsymbol{r}^{[d]}$$$.
Adjoint operator: Similar to the forward operator, $$$\frac{\partial \boldsymbol{A}^{\prime} \boldsymbol{y}}{\partial \boldsymbol{y}}=\boldsymbol{A}^{\prime}$$$ and $$$\frac{\partial \boldsymbol{A}^{\prime} \boldsymbol{y}}{\partial \boldsymbol{\omega}^{[d]}}=\imath \operatorname{diag}\left\{\boldsymbol{r}^{[d]}\right\} \boldsymbol{A}^{\prime} \operatorname{diag}\{\boldsymbol{y}\}$$$.
Frame operator: Combining the forward and adjoint operator and using the product rule yields $$$\frac{\partial \boldsymbol{A}^{\prime} \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{x}}=\boldsymbol{A}^{\prime} \boldsymbol{A}$$$ and $$$\frac{\partial \boldsymbol{A}^{\prime} \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{\omega}^{[d]}}=-\imath \boldsymbol{A}^{\prime} \operatorname{diag}\left\{\boldsymbol{A}\left(\boldsymbol{x} \odot \boldsymbol{r}^{[d]}\right)\right\}+\imath \operatorname{diag}\left\{\boldsymbol{r}^{[d]}\right\} \boldsymbol{A}^{\prime} \operatorname{diag}\{\boldsymbol{A} \boldsymbol{x}\}$$$. Again, as a fast approximation, we replace each $$$\boldsymbol{A}$$$ here with a NUFFT operator.
Experiments: We validated the accuracy and speed of different methods using two simple test cases: $$$\frac{\partial\left\|\boldsymbol{A}^{\prime} \boldsymbol{A} \boldsymbol{x}\right\|_{2}^{2}}{\partial \boldsymbol{\omega}^{[d]}}$$$ and $$$\frac{\partial\left\|\boldsymbol{A}^{\prime} \boldsymbol{A} \boldsymbol{x}\right\|_{2}^{2}}{\partial \boldsymbol{x}}$$$, where $$$\boldsymbol{x}$$$ is a cropped Shepp–Logan phantom with random additional phase, and the sampling pattern is an undersampled radial trajectory. We compared three settings: (1) auto-differentiation of NUFFT [7]. The table look-up operation is replaced by bi-linear interpolation to enable auto-differentiation, (2) auto-differentiation of NDFT, and (3) our approximation. (2) is the accurate gradient of NDFT because the gradient calculation only involves one exponential and one sum operation, with no accumulation error. Since NUFFT is only an approximation of NDFT, we cannot directly regard NDFT's Jacobian as NUFFT's Jacobian. If the NUFFT operation is accurate enough, however, (2) can be a good approximation of NUFFT's Jacobian matrix.
We also applied (1) and (3) to the sampling pattern optimization problem. The optimization workflow is similar to the one described in [3].
Results
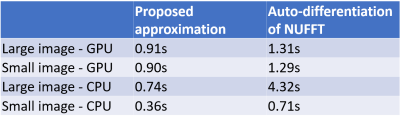
One example of the validation experiment is shown in Figure 1 and 2. For the gradient w.r.t. the image $$$\boldsymbol{x}$$$, three methods yield similar results. While for the kspace sampling pattern $$$\boldsymbol{\omega}$$$, the auto-differentiation has large deviance from the exact NDFT. If the phase of the complex-valued image $$$\boldsymbol{x}$$$ is not purely random, the three methods still have similar results.Table 1 compares the computation time. The CPUs and GPUs deployed are Intel Xeon Gold 6138 and Nvidia RTX2080Ti.
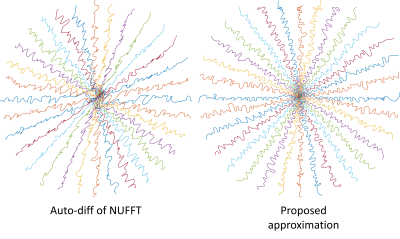
In Figure 3, our approximation leads to a learned trajectory consistent with intuition: sampling points should not be clustered or too distant from each other. We also compared the reconstruction quality of the two trajectories. The training and test set are from the fastMRI initiative [8] brain dataset and the reconstruction algorithm is the non-Cartesian version of MoDL [9]. The quantitative reconstruction results also demonstrate significant improvement (average SSIM: 0.930 vs. 0.957).
Conclusion
The proposed approximation method achieved improved speed and accuracy for the Jacobian calculation of the NUFFT operation. For further study, field inhomogeneity should also be incorporated into the model.Acknowledgements
This work is supported in part by NIH Grants R01 EB023618 and U01 EB026977, and NSF Grant IIS 1838179.References
[1] Aggarwal HK, Jacob M. Joint Optimization of Sampling Patterns and Deep Priors for Improved Parallel MRI. InICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2020 May 4 (pp. 8901-8905). IEEE.
[2] Bahadir CD, Dalca AV, Sabuncu MR. Learning-based optimization of the under-sampling pattern in MRI. In International Conference on Information Processing in Medical Imaging 2019 Jun 2 (pp. 780-792).
[3] Weiss T, Senouf O, Vedula S, Michailovich O, Zibulevsky M, Bronstein A. PILOT: Physics-informed learned optimal trajectories for accelerated MRI. arXiv preprint arXiv:1909.05773. 2019 Sep.
[4] Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE transactions on signal processing. 2003 Jan 22;51(2):560-74.
[5] Dale B, Wendt M, Duerk JL. A rapid look-up table method for reconstructing MR images from arbitrary k-space trajectories. IEEE transactions on medical imaging. 2001 Mar;20(3):207-17.
[6] Luo T, Noll DC, Fessler JA, Nielsen JF. Joint Design of RF and gradient waveforms via auto-differentiation for 3D tailored excitation in MRI. arXiv preprint arXiv:2008.10594. 2020 Aug 24.
[7] Muckley MJ, Stern R, Murrell T, Knoll F. TorchKbNufft: A High-Level, Hardware-agnostic Non-Uniform Fast Fourier Transform. ISMRM Workshop on Data Sampling & Image Reconstruction. 2020.
[8] Zbontar J, Knoll F, Sriram A, Murrell T, Huang Z, Muckley MJ, Defazio A, Stern R, Johnson P, Bruno M, Parente M. fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:1811.08839. 2018 Nov 21.
[9] Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging. 2018 Aug 13;38(2):394-405.
Figures
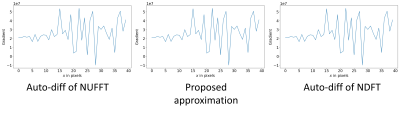
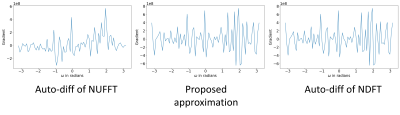
Figure 2. The gradient w.r.t. $$$\boldsymbol{\omega}$$$. The proposed approximation better matches the gradient of the NDFT.