Introduction

3D MP-SSFP has recently been introduced as an imaging sequence for use with inhomogeneous magnetic fields¹. While MP-SSFP is highly tolerant to the magnetic field inhomogeneity, it requires a broadband excitation RF pulse to cover the widely distributed frequency range over the 3D imaging volume, which limits achievable flip angles (i.e, SNR) due to severe SAR limitations. In this study, we introduce optimal flip angle and RF phase in 3D MP-SSFP to maximize SNR under the SAR limitations.

Methods

In MP-SSFP, one RF pulse in every N_MP pulses is replaced with an acquisition window to acquire refocused spin- and stimulated echoes, and as such, each repetition period contains N_MP-1 RF pulses. To constrain SAR in MP-SSFP, SAR regularization was introduced in the numerical optimization; optimal flip angle, $$$\mathbf\alpha = (\alpha_0, ..., \alpha_{N_{MP}-2})$$$, and RF phase, $$$\mathbf\phi = (\phi_0, ..., \phi_{N_{MP}-2})$$$, were determined by solving the following:
$$\mathbf\alpha , \mathbf\phi =arg\min_{\hat{\mathbf\alpha},\hat{\mathbf\phi}}F(\hat{\mathbf\alpha}, \hat{\mathbf\phi})$$,
$$ F(\mathbf\alpha,\mathbf\phi)=-|M_{ss}|+\lambda\alpha_{std}^2$$,
$$ \alpha_{std}=\sqrt{\sum_{i=0}^{N_{MP}-2}\alpha_i^2/N_{MP}}$$,
where M_ss is the steady-state transverse magnetization computed with extended phase graph simulation^2,3, α_std is the “standardized” flip angle representing RF energy per unit time (α_std² $$$\propto$$$ SAR) and λ is a regularization parameter to enforce the SAR constraint. The minimization problem was solved with a simplex search method⁴.

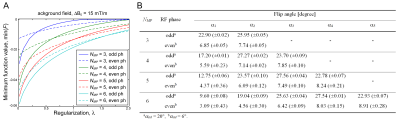
Two types of optimal RF phase $$$\mathbf\phi$$$ were obtained depending on λ: $$$\phi_i=2n\pi\cdot i/N_{MP}$$$ and $$$\phi_i=(2n-1)\pi\cdot i/N_{MP},(^\forall n\in \mathbb{Z})$$$ with strong and weak regularization, respectively. The two phase conditions were referred to as “even” and “odd” phase hereafter. The even and odd optimal phase conditions were consistently observed regardless of the background inhomogeneous field and the missing pulse interval N_MP tested in this study (Fig.1A). Optimal flip angle α was set to the solution that provided α_std=6º and 20º for the even and odd phase, respectively (Fig.1B).

MRI studies were conducted with a Siemens Prisma 3T MRI using a 64ch head/neck coil. The optimal flip angle and phase were first tested with an agar gel phantom. Then, in vivo human brain imaging was performed with healthy volunteers under an IRB approved protocol. The MP-SSFP sequence parameters used in MRI experiments (and the optimization of flip angle and phase) were: τ=5 ms, N_MP=3-6, α_std=6º and 20º, flattened hyperbolic secant pulse (HS2)⁵ with 1.6-ms duration and 12 kHz bandwidth and readout bandwidth=46 kHz. A linear inhomogeneous field ΔB₀ of 10, 15 or 20 mT/m was turned on during the entire MP-SSFP scan with the z channel of the gradient coil set. The linear inhomogeneous field was partly compensated during excitation and readout by modulating the z gradient amplitude. MP-SSFP scans with a constant flip angle for all RF pulses were conducted for comparison.

Results

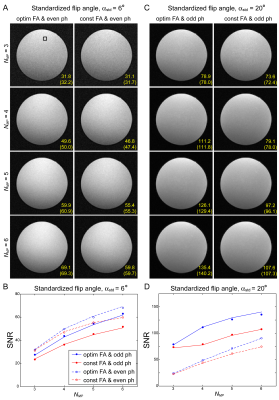
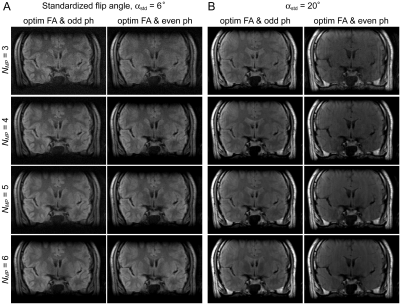
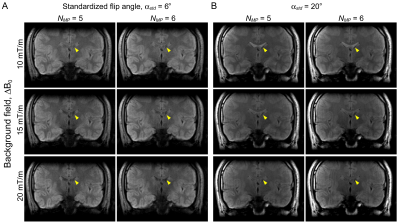
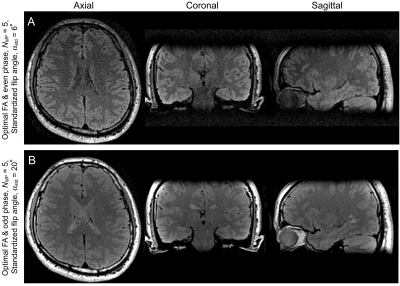
With α_std=6º, SNR was 1.02/1.06/1.08/1.14 times higher for N_MP = 3/4/5/6 with optimal flip angles than with constant flip angles, which matched well with the simulation results (Fig.2A). As observed in simulation, even RF pulse phase provided higher SNR than odd RF phase in the low flip angle/SAR condition (Fig.2B). With the high flip angle of α_std=20º, optimal flip angles improved SNR by a factor of 1.07/1.41/1.30/1.26 relative to constant flip angles for N_MP = 3/4/5/6 (Fig.2C). In the high flip angle/SAR condition, odd RF phase achieved higher SNR than even RF phase (Fig.2D).

To demonstrate image contrasts, brain imaging was conducted with optimal flip angle of α_std=6º or 20º and odd or even RF phase (Fig.3). SAR was 5-6% and 50-60% of the limit with the vendor provided SAR monitor for α_std=6º and 20º, respectively. With α_std=6º, although SNR increased along with an increase of N_MP, image contrast was similar regardless of RF phase and N_MP (Fig.3A). With α_std=20º, odd phase provided stronger contrasts between gray and white matters (Fig.3B). Image contrasts with α_std=20º and even RF phase were mostly T1-weighted. The background inhomogeneous field, ΔB₀, tested herein made minimal impact on image contrasts of brain tissues regardless of RF phase, but CSF signal intensities decreased along with an increase of ΔB₀ due to its high ADC value (Fig.4). High resolution imaging was performed with the SNR optimal setting for α_std=6º and 20º (Fig.5). While the low flip angle (α_std=6º) achieved stronger image contrasts in brain tissues, SNR was conspicuously higher with α_std=20º than with α_std=6º.

Discussion

The standardized flip angle α_std is an SAR-based function (α_std² $$$\propto$$$ SAR) such that MP-SSFP scans with a constant α_std entails identical SAR. Therefore, the optimal flip angle and phase herein achieved an up to 41% increase of SNR under the fixed SAR conditions.

In previous works^1,6, two RF phase settings were introduced: constant and alternate phase. When N_MP is odd, the even and odd RF phase from optimization in this study matches constant and alternate RF phase in the previous works, respectively. With N_MP = an even number, either constant or alternate RF phase matches the even RF phase such that the two RF phase settings resulted in an identical |M_ss| in the previous report¹.

Conclusion

Optimal flip angle and RF phase numerically determined in this study improved SNR under the fixed SAR conditions and provided strong image contrasts in brain tissues at 3T.

Acknowledgements

This work was supported by NIH grants U01EB025153 and P41EB027061.