0900
B1-gradient based MRI using Frequency-modulated Rabi Encoded Echoes (FREE)
Efraín Torres1,2, Taylor Froelich2, Lance DeLaBarre2, Michael Mullen2, Gregory Adriany2, Alberto Tannús3, Daniel Cosmo Pizetta3, Mateus Jose Martins3, and Michael Garwood2
1Biomedical Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Centro de Imagens e Espectroscopia por Ressonância Magnética - CIERMag - Sao Carlos Physics, São Carlos, Brazil
1Biomedical Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Centro de Imagens e Espectroscopia por Ressonância Magnética - CIERMag - Sao Carlos Physics, São Carlos, Brazil
Synopsis
Gradient coils reduce available bore space, incur costs, and create acoustic noise, but their encoding ability requires them to be present in MRI. The encoding strategy introduced here (FREE) removes the reliance on these coils by using a B1-gradient to create a spatially-dependent nutation frequency. Double spin-echoes created with adiabatic full-passage pulses generate magnetization phase proportional to the difference in their time-bandwidth products (R). Modulating the R-value of one of these π pulses traverses k-space similar to standard MRI. Adiabatic pulses make this approach highly tolerant to B0 and B1 inhomogeneity. A family of new sequences using FREE is presented.
Purpose
The MRI scanner is an invaluable clinical tool, yet there are great health care disparities with this technology. Due to its cost and infrastructure requirements, MRI is often inaccessible to people with lower socioeconomic status. In an effort to reduce cost and increase portability, we have pursued techniques that eliminate the need for certain expensive, large components of the MRI scanner. Specifically, with only RF field (B1) gradients for spatial encoding, B0 gradient coils and amplifiers can be eliminated. Previous RF imaging methods1, 2, 3 have been limited by their intolerance to resonance offset and B0 inhomogeneity, which is incompatible with the goal of employing small magnet configurations. Here, a family of B1-encoded spin-echo sequences are presented as a solution to this problem. The method is dubbed FREE for Frequency-modulated Rabi Encoded Echoes.Methods
In FREE, spatial information is encoded similar to conventional phase-encoding, although the gradient is in B1, rather than B0. FREE is accomplished by exploiting properties of any frequency-modulated adiabatic full-passage (AFP) pulse (e.g., Hyperbolic Secant (HS)4). AFP pulses produce uniform flip angle of π, even with large variations in the magnitudes of B1 and B05. When AFP pulses of differing time-bandwidth products (R) are used in a double spin-echo sequence, the phase of the echo signal can be made to be proportional the amplitude of the B1 field6. In FREE, the R-value of the generated pulse patterns are increased by increasing the pulse duration (Tp), while holding the pulse’s bandwidth (BW) constant. The maximum Rabi nutation frequency during the pulse is $$$\omega_{1}^{max} = \gamma B_{1}^{max}$$$ , where $$$\gamma$$$ is the gyromagnetic ratio. When $$$\omega_{1}^{max}$$$ is spatially dependent (i.e., in a B1 gradient), a spatially-dependent phase is imprinted on the spin-echo signal. Due to the AFP’s sweeping effective field, the total phase accrued by the end of a given π rotation is$$ \phi_{HS} = \pm \frac{Tp}{2}\int_{-1}^{1}\sqrt{(\omega_{1}^{max})^{2}sech^{2}(\beta \tau) + (\Omega - A \cdot tanh(\beta \tau))^{2}} d\tau \:(1)$$
where β is a truncation factor, set to sech( β ) = 0.01, Ω is resonance offset in rad/s, A = BW/2 in rad/s, τ is normalized time defined as 2t/Tp - 1 for 0 ≤ t ≤ Tp, and R = ATp/π. The sign of in Eq. 1 depends on the direction of the frequency sweep (e.g., from low to high). When varying the R of AFP pulses in a double spin-echo sequence (Fig. 1), the effect of B0-inhomogeneity (accounted for by Ω) is negated, while only a linear dependence on remains. The dependence of $$$\phi_{HS}$$$on $$$\omega_{1}^{max}(x)$$$ for double echoes produced with different R values is shown in Fig. 2. A direct relationship exists between the difference in R values (∆R) and the amount of phase encoding achieved, as described by Eqs. 2 and 3. For given field-of-view (FOV) and known B1 gradient, the value of ∆R that satisfies the Nyquist criterion can be determined. A k-space trajectory is achieved by repeated incrementation of ∆R. For given FOV and, ∆R for Cartesian sampling is calculated as
$$\Delta R = \frac{A}{\frac{d}{dx}[-C(\omega_{1}^{max}(x))]\cdot2 FOV} \: (2)$$
where
$$C(\omega_{1}^{max}(x)) =\left[ A^{2}\left(\frac{1}{\beta} log(\omega_{1}^{max}(x)) - 1 \right) + \frac{A}{2\beta}\left(\sqrt{(\omega_{1}^{max}(x))^2 - A^2}\right) tan^{-1}\left(\frac{2A \sqrt{(\omega_{1}^{max}(x))^2 - A^2}}{-2A^2 + (\omega_{1}^{max}(x))^2}\right) \right] \: (3)$$
Using multiple shots (Fig 1a), k-space is sampled by keeping the R of one of the pulses constant and varying the other by integer multiples of ∆R. The first shot has the greatest difference in R-values (Ro - Rmin). Defining N as the number of samples to be collected, and Ro as the R value of the non-changing pulse, then
$$R_{min} = R_{o} - \frac{N}{2} \Delta R \: (4)$$
Experimental and simulated studies utilized the following parameters: linear B1-gradient having $$$\omega_{1}^{max}(x)$$$ ranging from 0.25 to 2.5 kHz (simulations), and 0.25 kHz to 3.56 kHz (experiments), HS8 pulses (BW = 4 kHz), with maximum Tp = 10 ms, and R from 24.25 to 40, with ∆R = 0.25. Experiments were performed with the sequence seen in Fig. 1a. Data were acquired with a CIERMag Digital Magnetic Resonance Spectrometer8, configured for two Tx/Rx channels and operating at 1.5 Tesla (63.8 MHz), controlled by Python Magnetic Resonance Framework (PyMr9, 10, 11) and ToRM-Console12. Gradient-echo (GRE) and FREE reconstructions are compared.
Results
Simulated results (Fig. 4) demonstrate the ability of FREE to produce reconstructions which are similar to that of standard phase-encoding, until a large resonance offset (±2kHz) exists across the object. Experimental 1D images of the phantom (Fig. 5) show excellent agreement between FREE and frequency-encoded projections of the object, at least for positions nearest the coil.Discussion
The distortions observed in the simulation with large offset (±2kHz) are due to limited pulse bandwidth, and thus, simply increasing BW would remedy this. At locations far from the coil, the phantom was not visualized well with FREE, most likely due to poor adiabatic condition in this low region. In addition, the reconstruction was affected by the non-linear B1 of the surface coil. To remedy this, image distortion-correction algorithms might be applied in the future7.Conclusion
FREE enables phase-encoding with no B0 gradient coil. The sequences presented here show the potential for a new approach that enables the removal of gradient coils in future MRI system designsAcknowledgements
This work was supported by National Institute of Health grants P41 EB027061 and U01 EB025153, Schott Family Foundation, and the Minnesota Lions.References
- Hoult, D. I. "Rotating frame zeugmatography." Journal of Magnetic Resonance (1969) 33.1 (1979): 183-197.
- Canet, Daniel. "Radiofrequency field gradient experiments." Progress in Nuclear Magnetic Resonance Spectroscopy 30.1-2 (1997): 101-135.
- Sharp, Jonathan C., and Scott B. King. "MRI using radiofrequency magnetic field phase gradients." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 63.1 (2010): 151-161.
- Silver, Michael S., Richard I. Joseph, and David I. Hoult. "Highly selective π2 and π pulse generation." Journal of Magnetic Resonance (1969) 59.2 (1984): 347-351.
- Garwood, Michael, and Lance DelaBarre. "The return of the frequency sweep: designing adiabatic pulses for contemporary NMR." Journal of magnetic resonance 153.2 (2001): 155-177.
- Lee, Yoojin, et al. "New phase‐based B1 mapping method using two‐dimensional spin‐echo imaging with hyperbolic secant pulses." Magnetic resonance in medicine 73.1 (2015): 170-181.
- Mullen, Michael, and Michael Garwood. "Contemporary approaches to high-field magnetic resonance imaging with large field inhomogeneity." Progress in Nuclear Magnetic Resonance Spectroscopy 120 (2020): 95-108.
- Martins, M.J. ; Vidoto, Edson Luiz Gea ; Tannus, Alberto . Patent: “Espectrômetro para uso em sistemas de ressonância magnética e sistemas de ressonância magnética”. Process: BR102015000624-1, INPI - Instituto Nacional da Propriedade Industrial. Deposit date: 12 jan. 2015
- Pizetta D, Lourenço G, Silva D, Vidoto E, Martins M, Tannús A. “Magnetic resonance system configuration and editing tools”. (2015); Toronto, Canada, p667-668.
- Pizetta D, Shimada D, Falvo M, Souza P, Silva L,Bittencourt H,, Vidoto E, Martins M, Tannús A. Revista da Propriedade Industrial – RPI, n.2538, p.23. Software registry: “PyMR - a framework for programming magnetic resonance systems”. Process: BR512019001829-0. Registry date: 18 aug. 2017
- Pizetta, Daniel Cosmo. PyMR: a framework for programming magnetic resonance systems [thesis]. São Carlos: , Instituto de Física de São Carlos; (2018). doi:10.11606/T.76.2019.tde-06052019-103714.
- TANNÚS, A.; PIZETTA, D. C.; SILVA, D.M.D.D; VIDOTO, E.L.G; MARTINS, M. J. Revista da Propriedade Industrial – RPI, n.2365, p.350. Software registry: “Subsistema multiplataforma para controle de aquisição, visualização e organização de dados de espectrômetro digital de RM: ToRM Console”. Process: BR512015001485-4. Registry date: 07 dec. 2015.
Figures
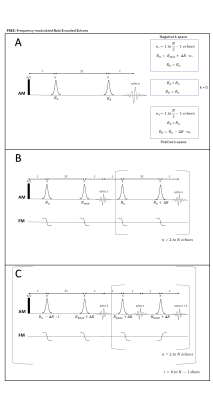
Fig. 1a) Multi-shot approach of FREE 1b) is a
single-shot approach. First double spin-echo pair has the greatest R-difference.
Subsequent π pulse pairs have a
difference of exactly ∆R incrementally
adding phase at each echo acquired. 1c) Multi-shot version of FREE, in
which all (odd and even) echoes are acquired. All pulses, except for the first, have Rbase +
∆R, where Rbase is any adiabatic R value. Further shots reduce the R value of the first pulse (Ro) by integer values of ∆R. The k-space
matrix is created by concatenating the data columns (shot number) with rows as
echo number.
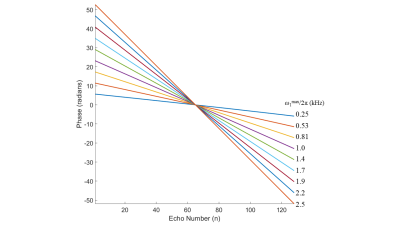
Linear increase in phase in accordance with echo number and
. Echo numbers correspond to differences in Ro
and the second R value used in the π pulse pair. The difference in
the values is equal to integer multiples of ∆R. Complete refocusing
is seen at echo 64, where the R values are equal (sampling k = 0). Sequence
in Fig. 1a was used.
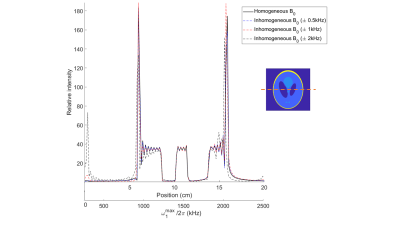
FREE simulated reconstruction (sequence Fig 1a) with varying resonance
offsets. The reconstruction has no significant errors until the bandwidth of
the pulse is reached.
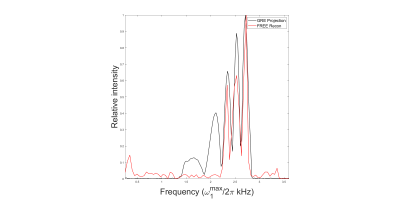
Phantom is a NMR tube with ~15 cm water doped with copper sulfate. Structure
was created in the phantom by purposefully creating a flip angle range. Comparison
of the GRE projection and FREE reconstruction. The x-axis represents nutation
frequency which has positional dependence due to the surface coil’s B1
gradient. The plane of surface coil is located on the right where
is the largest. Linearity of the B1
gradient decreases with distance from the coil. Good agreement between GRE and
FREE reconstructions is achieved except at the deeper location.