Introduction

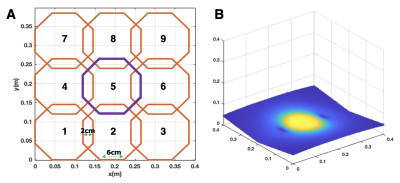
Recently, there has been a renewed interest in low-field MRI with the aim of building low cost systems to increase accessibility.^1,2 The cost and complexity of MRI systems can be reduced by eliminating B₀-gradient coils.³ To this end, we have developed a novel, low-field, open (Table-top) MRI system (Figure 1A) that allows for gradient-free imaging in a nonuniform B₀-field at 24mT. The low-field readout yields T2s long enough to obtain up to 800 echoes in 1 second (Figure 1B). This provides significant flexibility in designing RF encoding patterns that maximize scan efficiency. In the proposed system, we independently control the amplitude and phase of the RF transmit pulse to each element in a 3x3 planar array, to define encoding patterns analogous to that of nonlinear projections. Considering combinations that only apply RF pulses to 8 channels with amplitudes of 0 or 100%, and phase 0 or π leads to 2304 possible patterns, making it challenging to choose an appropriate subset for image encoding. Here we propose a metric for ranking and assembling a set of encodings with minimal correlation. Images simulated with this encoding set demonstrate the feasibility of performing Bloch-Siegert shift⁴ spatial encoding with typical nonlinear RF coil profiles.

Methods

Slice selection: The B₀-field of the Table-top system is generated by an electromagnet that can be dynamically controlled to achieve nonplanar slice selection. A single nonplanar slice containing uniform magnetic field strength (1MHz), that was on average 5cm from the bottom of the flat plane of the magnet was used in our 2D simulations.

Encoding scheme calculation: A 3x3 planar RF array coil was designed for Bloch-Siegert shift based encoding (Figure 2A). The B1-field generated by each coil element ($$$B1_c$$$) was computed using the “Biot-Savart magnetic Toolbox” in MATLAB.⁵ Figure 2B shows the B1-field of a coil element across the slice-profile used in our simulations. Using these B1-fields, encoding patterns were calculated according to the following equation:
$$B_1=\sum_1^nB1_c*A$$ where $$$n$$$ is the total number of transmit channels, and $$$A$$$ is a vector defining the amplitude and phase of the current passed to each channel.

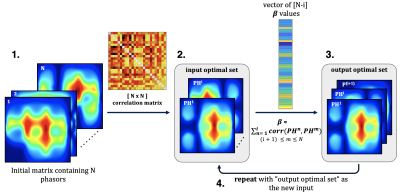
Data analysis and optimization: Bloch simulations were used to compute the phasors generated by each encoding pattern. The L2 norm of the unwrapped phasor in a 20cmx20cm area in the center of the FOV was used to quantify the total amount of encoding provided by each candidate phasor. After thresholding by L2 norm, an optimal set was built by recursively choosing the pattern that minimized β, a metric which reflects how much a pattern would increase the L2 norm of the overall correlation matrix (Figure 3). This was intended to choose a distinctive set of encodings, while minimizing redundancy in the acquired encodings.

Image reconstruction: We performed algebraic reconstruction of the MR signal generated by the encoding patterns using the conjugate gradient method for nonlinear encoding fields.⁶ The measured MR signal was calculated as:
$$s_n (τ)= ∫p(r)*C_n (r)*e^{i*ϕ_{BS}(r,τ) } dr$$ where $$$C_n (r)$$$ is the complex coil sensitivity profile, $$$p(r)$$$ is the phantom image, and $$$ϕ_{BS}$$$ is the phase distribution of the encoding pattern.

Results

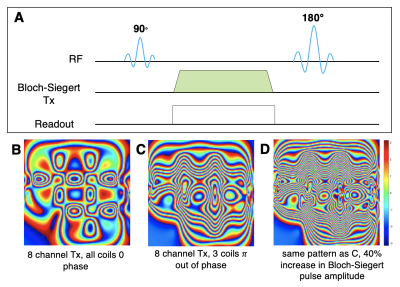
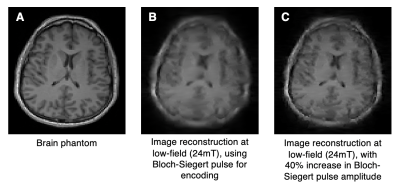
For the Bloch simulation experiments we used a spin-echo sequence with TE=16ms, T1=3000ms, T2=250ms, sampling rate of 0.023ms, and matrix size 128x128 voxels. The Bloch-Siegert transmit pulse was applied for 6ms (Figure 4A). As seen in Figure 4B-D, changing the phase offset or the amplitude of the applied Bloch-Siegert RF pulse creates distinct phase maps, with varying amounts of phase windings. We can also change the spatial shape of these patterns by selecting different subsets of coils for Bloch-Siegert transmission. These different patterns assign a signature phase evolution to each voxel in the image, that can then be recovered using our nonlinear reconstruction technique. 128 of the 2304 encoding patterns were selected (analogous to 128 projections), using the method described in the previous section, for image reconstruction. Figure 5 shows the reconstructed images of a high resolution brain scan.

Discussion

We have demonstrated the feasibility of performing nonlinear Bloch-Siegert shift based imaging on our low-field Table top MRI scanner, through simulation experiments. The overall image quality of the reconstructed images is excellent, with minimal blurring at the peripheries. The lower resolution at the edges is due to the fact that the encoding patterns were optimized for a region in the center of the FOV, and as such the phase winds more slowly outside this region. We can address this issue by either selecting encoding patterns that have been optimized for the entire FOV, or by increasing the amplitude of the applied Bloch-Siegert transmit pulse.

The simulation algorithm developed in this study allows us to robustly assess various encoding patterns, build optimal encoding schemes, and reconstruct MR images. This provides us with the freedom to generate and evaluate encoding patterns from any RF array coil. We are currently extending this to evaluate encoding patterns created from transmitting on different numbers of coils (3, 4, or 5 coils etc.), as well as expanding the range of phase offsets between coil elements.

Conclusion

In this study we have shown that Bloch-Siegert shift based nonlinear spatial encoding can be used to perform low-field MR imaging in a nonuniform B₀-field.

Acknowledgements

No acknowledgement found.