0894
The Design of an Acentric Cartesian Spiral Sampling with Partial Fourier for Highly Accelerated Single-breath-hold Isotropic 3-D Cardiac Cine
Yu Ding1, Qi Liu1, Jingyuan Lyu1, Yuan Zheng1, and Jian Xu1
1UIH America, Inc, Houston, TX, United States
1UIH America, Inc, Houston, TX, United States
Synopsis
We design a novel acentric spiral pattern and combine with partial Fourier to form a new sampling strategy in 3-D Cartesian acquisition. This new strategy was implemented and tested in isotropic 3-D single breath hold cardiac cine imaging with isotropic spatial resolution and whole heart coverage. Volunteer study shows that this new sampling strategy greatly reduced the number of samples and have acceptable image quality.
Introduction
Cardiac cine magnetic resonance imaging (MRI) is an important tool for the assessment of cardiac morphology and function [1]. Recently, the feasibility of highly accelerated 3-D single breath hold cine imaging has been demonstrated using a 3-D Cartesian spiral phyllotaxis acquisition pattern [2]. Partial Fourier is a common imaging technique to reduce MRI scan time by using k-space conjugate symmetry. It would be desirable to combine Cartesian spiral pattern with partial Fourier technique in pursuit of further acceleration. However, design of such imaging strategy is nontrivial because of conflicts between centric spiral patterns and acentric partial Fourier pattern in k-space. In fact, to the best of our knowledge, there is no publication attempting to combine these two techniques. In this study, a novel acentric Cartesian spiral pattern is designed and combined with partial Fourier to form a new acquisition strategy for single-breath-hold isotropic 3-D cardiac cine. This new acquisition strategy has been tested in volunteer study.Methods
The proposed method is illustrated in four sub-sections:Acentric spiral pattern generation:
Recall that traditional Archimedean spiral can be described by the equation in polar coordinate: $$$r = b + aθ$$$, where $$$r$$$ is the distance to the center of k-space; $$$θ$$$ is the angle; $$$a$$$ and $$$b$$$ are two parameters, which controls the curvature and the angular offset, respectively. The acentric spiral is generated using the following four steps: 1) generate an acentric grid corresponding to the k-space with partial Fourier; 2) apply an affine transform to the half space that partial Fourier is used, and move the geometric center of the grid to the center of k-space; 3) draw the Archimedean spiral described above on the transformed grid; and 4) apply an inverse affine transform to squeeze the centric spiral curve to acentric spiral curve. Then the centric spiral becomes acentric spiral. Figure 1 shows an example of the acentric spiral pattern.
Variable density sampling and k-space down-sampling:
The variable density sampling principle is adopted. The sampling probability density $$$\rho$$$ of each k-space point is inversely proportional to the distance to the k-space center $$$r$$$, i.e. $$$ρ = 1/(r + c)$$$, where $$$c$$$ is an adjustable parameter. The k-space is partitioned into 25 spiral arms, each arm is further partitioned into 15 segments. A simple criterion to determine the boundaries between partitions is used: make the sum of the sampling probability ρ for all points in each segment identical. After partition, the down-sampling pattern is generated by random selection of one point in each segment. The above process is repeated multiple times to generate a series of pre-determined down-sampling patterns for dynamic imaging.
ECG-gated acquisition and image reconstruction:
The data acquisition is prospectively ECG-triggered. In each RR interval, one arm is collected continuously according to the pre-determined pattern. After data acquisition, all k-space data is averaged to form a fully sampled center of k-space. The coil sensitivity map is calculated using the ESPIRiT method [3]. The raw data is reconstructed using compressed sensing, and the spatial-temporal TV is used as $$$L1$$$ regularization.
Volunteer study setup:
The proposed technique was implemented with a bSSFP sequence. All the studies were conducted on a 3.0 T scanner (uMR 790, United Imaging Healthcare, Shanghai, China) with a 24-channel cardiac coil. The volunteer was instructed to hold breath during the scan for 25 heart beats. Imaging parameters are: FA = 45 deg, FOV = 300×280×130 mm , matrix = 144×128×64 (interpolated to 144×134×64, with 75% Partial Fourier in phase-encoding and partition-encoding direction), bandwidth = 1200Hz/pixel, TR/TE = 2.85/1.31 ms.
Results
In the current study setup, 3-D cardiac cine was acquired in 20 seconds, achieving whole heart coverage with 2.1 mm3 isotropic spatial resolution in the volunteer study without significant visible artifacts. The effective acceleration rate was more than 17-fold. Figure 2 shows eight mid-short axis slices in systole and diastole of a volunteer.Discussion
We have developed a new sampling strategy in 3-D Cartesian acquisition using the combination of acentric spiral trajectory and partial Fourier. The new sampling strategy greatly reduced the total number of samples. Comparing to centric spiral trajectory without partial Fourier, the proposed method reduces the total number of samples by more than 40%. Preliminary volunteer test shows that the proposed method has acceptable image quality, which shows it is a promising approach for highly accelerated 3-D cardiac cine imaging with isotropic resolution and whole heart coverage. In this study, a relatively long breath-hold (25 heart beats, approximately 20 sec) was used. In the future study, we plan to further reduce the breath hold to around 15 seconds by increasing acceleration rate to improve patient comfort and increase compliance. More studies on volunteer and patients are warranted before it can be applied to clinical practice.Acknowledgements
No acknowledgement found.References
- Carr, James C, et al. Radiology 219.3 (2001): 828-834.
- Wetzl J, et al. MRMPBM, 2018, 31(1): 19-31.
- Uecker, M, et al. MRM 71.3 (2014): 990-1001.
Figures
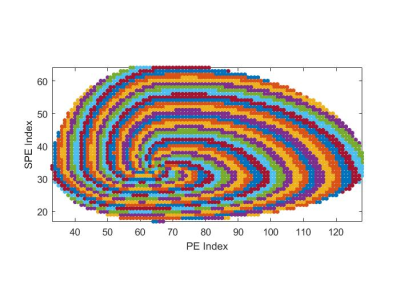
Figure 1. The acentric Cartesian spiral pattern in PE-SPE plane, with matrix size
128 x 64, 75% partial Fourier in both directions.

Figure 2. The upper row are eight short axis slices at the end of systole; the
lower row are the corresponding eight slices at the end of diastole. The
distance between two adjacent slices shown is 8.4 mm (four slice thickness).