0890

Towards Accelerating 3D ¹H-MRSI Using Randomly Undersampled Spatial and Spectral Spirals with Low-rank Subspaces

Yamin Arefeen¹, Borjan Gagoski^2,3, and Elfar Adalsteinsson^1,4,5
¹Massachusetts Institute of Technology, Cambridge, MA, United States, ²Fetal-Neonatal Neuroimaging and Developmental Science Center, Boston Children’s Hospital, Boston, MA, United States, ³Department of Radiology, Harvard Medical School, Boston, MA, United States, ⁴Harvard-MIT Health Sciences and Technology, Cambridge, MA, United States, ⁵Institute for Medical Engineering and Science, Cambridge, MA, United States

Synopsis

¹H Magnetic Resonance Spectroscopic Imaging (MRSI) suffers from low signal-to-noise ratio (SNR) and long acquisition times. Time-varying gradient trajectories reduce acquisition time by more efficiently sampling the k-space data. Meanwhile, a subspace approach to high-resolution MRSI (SPICE) elegantly enables high resolution MRSI despite low SNR. To accelerate 3D MRSI, we propose a randomly undersampled, time-varying, 3D-trajectory that synergizes with the SPICE-subspace framework by inducing incoherent aliasing across all four imaging dimensions. This enables ~3x acceleration in analytic experiments and ~2x acceleration in retrospectively undersampled phantom experiments with minimal degradation in image quality in comparison to fully sampled 3D-spiral MRSI.

Introduction

¹H Magnetic Resonance Spectroscopic Imaging (MRSI) suffers from low signal-to-noise-ratio (SNR) and long acquisition times. Time varying gradient trajectories,^1-4 compressed sensing,^5-7 and parallel imaging^8,9 reduce acquisition time; while, SPICE elegantly enables high resolution MRSI despite low SNR through low-rank priors.^10-12

Towards accelerating 3D-MRSI, we propose a randomly undersampled 3D-spiral trajectory that induces incoherent aliasing across all four imaging dimensions that can be resolved with subspace priors. Compared to fully sampled 3D-spiral MRSI, our method enables ~3x acceleration in single-channel analytic 3D MRSI experiments and ~2x acceleration in retrospectively undersampled phantom experiments with minimal degradation in image quality without parallel imaging.

Methods

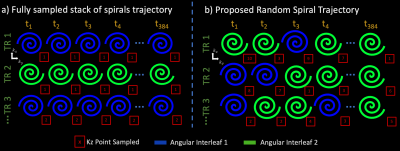
3D Randomly Undersampled Spiral MRSI Trajectory

Let $$$TR = A × T × P$$$ be the number of repetitions in a full 3D-spiral MRSI trajectory.^1,2 $$$k_x$$$ and $$$k_y$$$ are sampled with $$$A$$$ spiral angular interleaves, $$$k_z$$$ is sampled with $$$P$$$ cartesian partitions, and $$$t$$$ (time axis) is sampled by repeating each interleaf at a particular $$$k_z$$$ partition. The entire acquisition is repeated at $$$T$$$ shifted temporal interleaves.

To accelerate by a factor of $$$R$$$, the proposed trajectory samples $$$TR_{und} = \frac{TR}{R}$$$ repetitions. We build the proposed trajectory at a particular repetition:

Trajectory begins at $$$t_n$$$.
Pick one of the $$$A$$$ angular interleaves and a $$$k_z$$$ partition randomly.
At the current time sample $$$t_n$$$ and the chosen $$$k_z$$$ partition, acquire ($$$k_x$$$, $$$k_y$$$) samples with the chosen angular interleaf.
Set $$$t_{n+1} = t_n + timeSpiralAngularInterleaf$$$.
Repeat 2-4 until a measurement trajectory has been specified for the entire repetition.

We repeat until a trajectory has been specified for $$$TR_{und}$$$ repetitions. All $$$(k_x,k_y,k_z)$$$ points are measured at different temporal samples, inducing 4D-incoherent aliasing. Figure 1 compares schematic representations of the fully sampled and proposed trajectory.

SPICE Framework

$$$x(r,f) \in C^{M × N × P × F}$$$, the MRSI signal of interest, exists in a subspace:¹¹
$$x(r,f) = \sum_{m=1}^M s_m(r) \Phi_m(r) + \sum_{n=1}^N s_n(r) \Phi_n(r)$$
where $$$[\Phi_m(f)]_{m=1}^M$$$ / $$$[\Phi_n(f)]_{n=1}^N$$$ and $$$[s_m(r)]_{m=1}^M$$$ / $$$[s_n(r)]_{n=1}^N$$$ represent the subspaces and spatial coefficients for metabolite and nuisance signals.¹³ Subspaces are estimated from a calibration scan or learned from training data.^11,12 Typically $$$M,N << F$$$; thus SPICE resolves $$$x(r,f)$$$ amidst remarkably noisy measurements.

We accelerate by resolving the noise-like aliasing artifacts induced by our random 3D-spiral trajectory through subspace priors.

Forward Model

Let $$$F_{traj}$$$ be the operator which evaluates fourier measurements on our 3D randomly undersampled trajectory. Then solving,
$$argmin_{[s_m(r)]_{m=1}^M / [s_n(r)]_{n=1}^N} ||y - F_{traj}( \sum_{m=1}^M s_m(r) \Phi_m(r) + \sum_{n=1}^N s_n(r) \Phi_n(r))||_2$$
yields $$$x(r,f)$$$.

Experiments

Point-spread Function (psf) Experiments

Consider an acquisition with 160 × 160 × 80 mm field-of-view, 4 × 4 × 4 mm isotropic voxels, 1000 Hz spectral bandwidth, and 5.28 Hz spectral resolution. We compare psfs generated from full 3D-spiral MRSI (280 repetitions with 2 temporal interleaves, 7 angular interleaves, 20 partitions) to a uniformly undersampled spiral trajectory (by reducing angular interleaves) and our proposed trajectory; both with $$$R = 3$$$ (93 repetitions).

Analytic Phantom Experiments

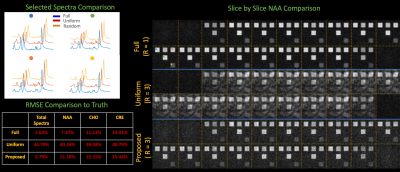
We compare reconstructions using the aforementioned trajectories on an analytic phantom with added noise. We specify 30 × 30 × 60 mm rectangular prisms doped with realistic concentrations of water, N-Acetylaspartate (NAA), creatine (Cr), and choline (Cho) amidst water suppression.

Subspaces were calibrated from a rapid 160 × 160 × 80 mm field-of-view, 10 × 10 × 10 mm resolution, full 3D-spiral acquisition (10 repetitions).

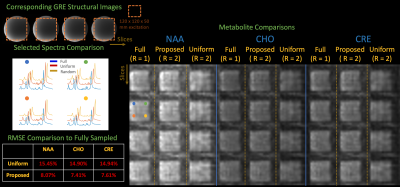
Scanner Phantom Experiments

We acquired fully sampled 3D-spiral spectroscopy data from a GE MRSI phantom¹⁴ with the following parameters: 160 × 160 × 80 mm field-of-view, 1 cc voxels, 1200 Hz spectral bandwidth, TR/TE = 30 / 1800 ms, 48 TR’s (1 average, 3 angular and 2 temporal interleaves, 8 partitions, 86 second acquisition), water suppression, and 120 × 120 × 50 mm volume-of-interest excitation using semiLASER pulses.¹

Fully sampled reconstructions are compared to uniform undersampling and our proposed trajectory, both with $$$R = 2$$$. Subspaces are calibrated retrospectively, from a full 3D-spiral acquisition with 160 × 160 × 80 mm field-of-view and 4cc isotropic voxels.

Note, we evaluate $$$R = 2$$$ (and not $$$R=3$$$) in the scanner phantom experiments, since we are currently constrained to lower imaging resolutions in which aliasing artifacts are more coherent using the chosen undersampling scheme.

Results

Figure 2 illustrates coherent aliasing of 15-20% from uniform undersampling, while the proposed trajectory spreads aliasing along all encoding dimensions with maximum and mean aliasing of .41% and .04%.

In Figure 3, the proposed trajectory achieves NAA maps and spectra which qualitatively match the fully sampled regime and achieves lower RMSE in comparison to uniform undersampling.

Scanner phantom experiments in Figure 4 illustrate that the proposed technique produces faithful metabolite maps and spectra and achieves at least ~2x reduction in RMSE across the metabolites

Conclusions

Combining SPICE and the proposed random 3D-spiral trajectory yields further acceleration compared to the fully sampled 3D-spiral MRSI acquisition by exploiting 4D-incoherent aliasing and temporal priors. We will further improve acceleration with parallel imaging and evaluate our technique in the presence of fat signals, and more realistic B₀ inhomogeneity, which will pave the way towards applying our methods to in-vivo experiments. Future work will also explore trajectories in this vast space of 4D-undersampling.

Acknowledgements

This work was supported in part by research grants NIH R01 EB017337, U01 HD087211, R01HD100009, and the NVidia Corporation for computing support. In addition, this material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. 1122374. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

References

1. Andronesi OC, Gagoski BA, Sorensen AG. Neurologic 3D MR spectroscopic imaging with low-power adiabatic pulses and fast spiral acquisition. Radiology. 2012;262: 647–661.

2. Adalsteinsson E, Irarrazabal P, Topp S, Meyer C, Macovski A, Spielman DM. Volumetric spectroscopic imaging with spiral-based k-space trajectories. Magn Reson Med. 1998;39: 889–898.

3. Posse S, Dager SR, Richards TL, Yuan C, Ogg R, Artru AA, et al. In vivo measurement of regional brain metabolic response to hyperventilation using magnetic resonance: proton echo planar spectroscopic imaging (PEPSI). Magn Reson Med. 1997;37: 858–865.

4. Steel A, Chiew M, Jezzard P, Voets NL, Plaha P, Thomas MA, et al. Metabolite-cycled density-weighted concentric rings k-space trajectory (DW-CRT) enables high-resolution 1 H magnetic resonance spectroscopic imaging at 3-Tesla. Scientific Reports. 2018. doi:10.1038/s41598-018-26096-y

5. Cao P, Wu EX. Accelerating phase-encoded proton MR spectroscopic imaging by compressed sensing. J Magn Reson Imaging. 2015;41: 487–495.

6. Nassirpour S, Chang P, Avdievitch N, Henning A. Compressed sensing for high-resolution nonlipid suppressed 1 H FID MRSI of the human brain at 9.4T. Magnetic Resonance in Medicine. 2018. pp. 2311–2325. doi:10.1002/mrm.27225

7. Chatnuntawech I, Gagoski B, Bilgic B. Accelerated 1H MRSI using randomly undersampled spiral‐based k‐space trajectories. Magnetic resonance. 2015. Available: https://onlinelibrary.wiley.com/doi/abs/10.1002/mrm.25394

8. Lin F-H, Tsai S-Y, Otazo R, Caprihan A, Wald LL, Belliveau JW, et al. Sensitivity-encoded (SENSE) proton echo-planar spectroscopic imaging (PEPSI) in the human brain. Magnetic Resonance in Medicine. 2007. pp. 249–257. doi:10.1002/mrm.21119

9. Tsai S-Y, Otazo R, Posse S, Lin Y-R, Chung H-W, Wald LL, et al. Accelerated proton echo planar spectroscopic imaging (PEPSI) using GRAPPA with a 32-channel phased-array coil. Magnetic Resonance in Medicine. 2008. pp. 989–998. doi:10.1002/mrm.21545

10. Ma C, Lam F, Ning Q, Johnson CL, Liang Z-P. High-resolution 1H-MRSI of the brain using short-TE SPICE. Magn Reson Med. 2017;77: 467–479.

11. Lam F, Ma C, Clifford B, Johnson CL, Liang Z-P. High-resolution 1H-MRSI of the brain using SPICE: data acquisition and image reconstruction. Magn Reson Med. 2016;76: 1059–1070.

12. Lam F, Li Y, Guo R, Clifford B, Liang Z-P. Ultrafast magnetic resonance spectroscopic imaging using SPICE with learned subspaces. Magn Reson Med. 2020;83: 377–390.

13. Ma C, Lam F, Johnson CL, Liang Z-P. Removal of nuisance signals from limited and sparse 1H MRSI data using a union-of-subspaces model. Magn Reson Med. 2016;75: 488–497.

14. Imaging B. 2152220 MRS Sphere with Solution Phantom for GE Closed MRI. [cited 6 Dec 2020]. Available: https://parts.blockimaging.com/2152220-mrs-sphere-with-solution-phantom-for-ge-closed-mri

Figures

Figure 1: Schematic view of (a) the fully sampled 3D-spiral MRSI trajectory and (b) our proposed randomly undersampled trajectory. For demonstration purposes, we assume 1 temporal interleaf. In (a), the same angular interleaf and $$$k_z$$$ point is sampled at each timepoint in a TR. The proposed (b) trajectory samples random angular interleaves and $$$k_z$$$ points during each TR and can be accelerated by reducing the number of TR’s. Our proposed trajectory takes advantage of the 4D-encoding space by spreading incoherent aliasing across spatial and spectral dimensions.

Figure 2: Impulse responses of the fully sampled, uniformly undersampled ($$$R = 3$$$), and proposed undersampling trajectory ($$$R = 3$$$). Both the full and the uniform acquisition schemes sample the temporal dimension at the Nyquist rate, thus making their impulse response to be concentrated around the center (DC) partition and spectral point. The uniformly undersampled trajectory exhibits large structured aliasing, while the proposed trajectory well matches the fully sampled impulse around DC, by spreading incoherent aliasing amongst all dimensions.

Figure 3: Visualization of NAA, RMSE comparison of metabolites and total spectra on image support, and illustration of example spectra comparing subspace-based reconstructions with full 3D-spiral MRSI, uniform undersampled (R = 3) stack of spirals, and the proposed trajectory (R = 3) simulated from the analytic phantom. The proposed trajectory yields similar spectra and NAA maps to the fully sampled acquisition and achieves significantly reduced RMSE values in comparison to uniform undersampling.

Figure 4: Metabolites maps, RMSE on image support, and example spectra from subspace reconstructions of fully sampled , uniformly undersampled (R = 2), and undersampled with the proposed trajectory (R = 2) on a spectroscopy phantom containing physiological concentrations of the major brain metabolites. The proposed trajectory yields similar spectra and metabolite maps to the fully sampled acquisition and achieves ~2x reduction in RMSE across the metabolites in comparison to uniform undersampling.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0890