0888
Elliptical shells: a fast single-shot 3D readout for Arterial Spin Labeling perfusion imaging
Joseph G. Woods1, Divya Bolar1, and Eric C. Wong1
1Department of Radiology, University of California San Diego, San Diego, CA, United States
1Department of Radiology, University of California San Diego, San Diego, CA, United States
Synopsis
Single shot 3D acquisitions are ideal for ASL because they provide insensitivity to motion and allow for effective background suppression. Current state of the art implementations use stack-of-spiral FSE based imaging for time efficiency and insensitivity to resonance offsets. We introduce here a further improvement in time efficiency by using spirals that are designed to approximate a spherically symmetrical variable density function. Spirals are constrained to elliptical shells, and are numerically optimized for time efficiency. An example trajectory is twice as fast as a cylindrical stack-of-spirals with similar density parameters (excluding refocusing time), and results in high quality ASL images.
Introduction
Arterial spin labeling is ideally acquired with a 3D readout, ensuring uniform background suppression and a single post-labeling delay across the image volume. Segmented fast spin-echo (FSE) 3D readouts are recommended, because the long acquisition times of single-shot 3D readouts can result in severe T2-related through-plane blurring.1 However, readout segmentation limits temporal resolution and increases sensitivity to subject motion. Recent approaches to reduce the readout duration of single-shot 3D readouts include 3D variable-density stack-of-spirals2 and 3D-GRASE with 2D-CAPIRINHA sampling3 using parallel imaging reconstruction. Further improvements have been achieved by varying the undersampling patterns across averages to create temporal incoherence of undersampling aliasing, which can then be exploited by compressed sensing reconstructions4,5. In this work, we introduce a time-efficient single-shot 3D FSE readout with a spherically symmetrical variable density and spiral in-out shells to more efficiently cover k-space than previous trajectories.Methods
The proposed trajectory approximates a spherically symmetrical variable density function. Any density function can be used, but we have used a density function with a central sphere r<rFS that is fully sampled, with a Gaussian transition to a minimum density ρmin given by ρ(r>rFS)=ρmin+(1-ρmin)e-(r-rFS)2/(σ*σ) for normalized radius r. The geometry of the trajectory is outlined in Figure 1. Each spiral arm is constrained to an ellipsoid of revolution about the z axis. XY and Z axes of the ellipsoids are defined by sets Kxymax and Kzmax and each ellipsoid is described by kxy=Kxymax*sin(θ) and kz=Kzmax*cos(θ) where θ is an elliptical parameterization of the polar angle. The pitch of the spirals was adjusted at every point such that the voronoi patch (approximated by a rectangle) was of size (dkxy*dkz)/ρ(r) where dkxy=1/FOVxy and dkz=1/FOVz. For given sets Kxymax and Kzmax, the local radial dimension of the patch (dkr in the Figure) is fixed by the geometry of the ellipsoids, and the local spiral pitch (dkθ in the Figure) is calculated to produce a voronoi patch of the size noted above. The set Kzmax was fixed with spacing dkz for r<rFS, with the remaining elements evenly distributed between r=rFS and r=1. The set Kxymax was initialized to the range [1,1.2], but was then numerically optimized so that the minimum duration6 of every spiral was equal. The spherical distributed spiral7 is a special case of this trajectory in which the density is uniform and Kxymax of all ellipses are set to kmax.Two trajectories were generated for this proof of principle, and are shown in Figure 2. One follows the resolution, FOV, and density parameters from2: FOV=216x216x144mm3, rFS=0.2, σ=0.2, Rkmax=12.5; while the other uses more uniform density with lower acceleration: FOV=151x151x101mm3, rFS=0.01, σ=0.2, Rkmax=4. For both, the target resolution was 3x3x3mm3, echo-train-length (ETL) 24, and excited slab thickness 144mm. These were compared to a commercial fully sampled stack-of-spirals acquisition with 8 segments, FOV 216x216x144mm3, resolution 4x4x4mm3, ETL 44 (4x slice-oversampling)8.
In vivo data was acquired at 3T using a 32-channel head-coil on a single volunteer with PCASL labeling: 1.45s label duration, 1.525s post-labeling delay. 14 tag/control pairs were acquired for the elliptical shell trajectories, while 1 tag/control pair was acquired for the stack-of-spirals readout. The scan durations were approximately 2 minutes each and included an M0 scan.
The data was reconstructed with the BART toolbox9 and non-Cartesian GRAPPA10. First, complex subtraction and averaging was performed. The stack-of-spirals data was reconstructed using the FFT across partitions and non-uniform fast Fourier transform (NUFFT) with sampling density weighting11 in-plane, before root-sum-of-squares (rss) coil combination. Two approaches were used for the elliptical shells data: (1) non-Cartesian GRAPPA with rss coil combination and (2) compressed sensing using the FISTA algorithm12 with l1-wavelet regularisation (λ=0.005) with ESPIRiT13 derived coil sensitivities. A 4s low-resolution Cartesian prescan was used for GRAPPA calibration and coil sensitivity estimation.
Results
ASL difference images are shown in Figure 3. Preliminary results show better image quality using the CS reconstruction than the GRAPPA reconstruction for both trajectories. Images acquired using the elliptical spirals were comparable to the fully sampled segmented stack of spirals, except for signal dropout that was prevalent in the inferior slices.Discussion
We report here an initial implementation of a new spherical spiral FSE based trajectory for single shot whole brain imaging at 3mm isotropic resolution. The spiral duration for trajectory 1 was 5.1ms, which is less than half of the spiral duration for a similar cylindrical stack of spiral implementation2, and should therefore reduce the T2 related signal modulation (and hence blurring) associated with long echo trains. We plan a more direct comparison with this approach in ongoing work.Acknowledgements
This work was partially funded by GE Healthcare. Thanks to Marc Lebel of GE Healthcare for providing base source code. Divya S. Bolar is supported by an RSNA Resident/Fellow Grant.References
- Alsop DC, Detre JA, Golay X, et al. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn. Reson. Med. 2015;73:102–116 doi: 10.1002/mrm.25197.
- Chang Y V., Vidorreta M, Wang Z, Detre JA. 3D-accelerated, stack-of-spirals acquisitions and reconstruction of arterial spin labeling MRI. Magn. Reson. Med. 2017;78:1405–1419 doi: 10.1002/mrm.26549.
- Boland M, Stirnberg R, Pracht ED, et al. Accelerated 3D-GRASE imaging improves quantitative multiple post labeling delay arterial spin labeling. Magn. Reson. Med. 2018;80:2475–2484 doi: 10.1002/mrm.27226.
- Munsch F, Taso M, Zhao L, et al. Rotated spiral RARE for high spatial and temporal resolution volumetric arterial spin labeling acquisition. Neuroimage 2020;223:117371 doi: 10.1016/j.neuroimage.2020.117371.
- Spann SM, Shao X, Wang DJ, et al. Robust single-shot acquisition of high resolution whole brain ASL images by combining time-dependent 2D CAPIRINHA sampling with spatio-temporal TGV reconstruction. Neuroimage 2020;206:116337 doi: 10.1016/j.neuroimage.2019.116337.
- Lustig M, Kim S-J, Pauly JM. A fast method for designing time-optimal gradient waveforms for arbitrary k-space trajectories. IEEE Trans. Med. Imaging 2008;27:866–873 doi: 10.1109/TMI.2008.922699.
- Turley DC, Pipe JG. Distributed spirals: A new class of three-dimensional k -space trajectories. Magn. Reson. Med. 2013;70:413–419 doi: 10.1002/mrm.24475.
- Dai W, Robson PM, Shankaranarayanan A, Alsop DC. Reduced resolution transit delay prescan for quantitative continuous arterial spin labeling perfusion imaging. Magn. Reson. Med. 2012;67:1252–1265 doi: 10.1002/mrm.23103.
- Tamir JI, Ong F, Cheng JY, Uecker M, Lustig M. Generalized Magnetic Resonance Image Reconstruction using The Berkeley Advanced Reconstruction Toolbox. ISMRM Work. Data Sampl. Image Reconstr. 2016.
- Luo T, Noll DC, Fessler JA, Nielsen J. A GRAPPA algorithm for arbitrary 2D/3D non‐Cartesian sampling trajectories with rapid calibration. Magn. Reson. Med. 2019;82:mrm.27801 doi: 10.1002/mrm.27801.
- Fessler JA, Sutton BP. Nonuniform fast fourier transforms using min-max interpolation. IEEE Trans Signal Process 2003;51:560–574.
- Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009;2:183–202 doi: 10.1137/080716542.
- Uecker M, Lai P, Murphy MJ, et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71:990–1001 doi: 10.1002/mrm.24751.
Figures
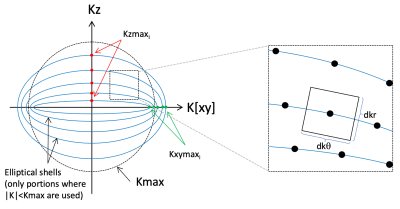
Generation of elliptical shells trajectory. Each spiral is confined to the surface of an ellipsoid of revolution about the Z axis. Ellipsoid i is defined by axes Kzmaxi and Kxymaxi. The dimensions of the voronoi patch are dkr*dkθ, as shown. For a given set of Kzmax and Kxymax, dkr is determined by the local geometry of the elliptical shells, and the spiral pitch dkθ is adjusted to produce a voronoi patch of the desired area for the local sampling density (see text).
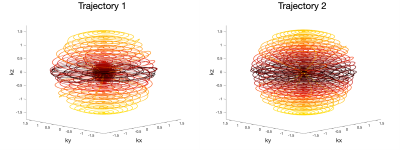
The two elliptical shells trajectories generated. Centric ordering was used across the FSE echo train, so echoes proceed form dark to light in these plots.
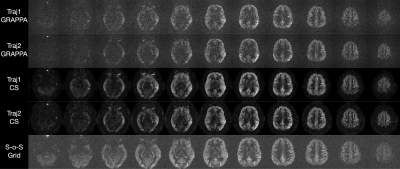
PCASL difference images from the two
trajectories shown in Figure 2, as well as a fully sampled segmented
stack of spiral acquisition.