0885
Mono-planar T-Hex EPI1Institute for Biomedical Engineering, ETH Zurich, Zurich, Switzerland
Synopsis
In this work, we show high-resolution stacks of EPIs on a tilted hexagonal grid. The scheme provides flexibility in balancing readout and scan time, thereby allowing for high-quality images in a temporal resolution regime suitable for fMRI. 0.7 mm whole-brain coverage is achieved in below 5s.
Introduction
Time-efficient MR scanning of 3D volumes with high spatial resolution is aimed at in a variety of applications like QSM, generic T2* weighted imaging, ASL, or functional MRI(1–7). 3D Fourier encoding lends itself to this task: it provides high SNR due to data acquisition from the entire volume while being amenable to undersampling by optimal PI acceleration in all three dimensions. One straightforward and widespread encoding strategy for this purpose is to stack EPI readouts in 3D k-space(8), covering one k-space plane at a time by a 2D trajectory. This is possible up to a certain resolution limit, beyond which covering an entire k-space plane would take too long for a single shot. The reasonable readout duration is limited by T2* decay(9) and intra-voxel dephasing due to static B0 non-uniformity. For higher resolution with stacks of EPIs, the common option is to cover each k-space plane by multiple, interleaved readouts. However, integer increments of the number of interleaves cause abrupt sequence changes as the targeted resolution increases, most so at few shots per plane. Furthermore, the overhead for other sequence modules such as RF excitation, saturation, and spoiling has to be repeated for every shot and makes a multiplication in the number of shots unattractive since this entails an increase in the total scan time. The described problem of covering each k-space plane with more than one shot is somewhat related to the challenge of sampling more than one k-space plane with each shot. The latter case has been tackled using tilted hexagonal grids as a basis for stacked spirals and EPIs (T-Hex)(10). It has been shown that the T-Hex concept in a slightly modified version can also be used in a high-resolution scenario – that is to say, to distribute k-space volume onto more spiral shots than one per plane. In this case, it serves as a method to balance readout length and scan-time more flexibly than it has been possible so far(11). In the present work, the mono-planar T-Hex concept is applied to EPIs achieving a 0.7x0.7x2mm3 resolved whole-brain scan in 4.3s.Methods
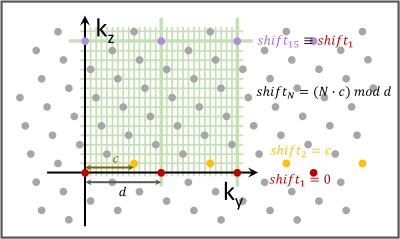
T-Hex: An excerpt of the tilted hexagonal grid(10,12) underlying a stack of EPIs is exemplarily shown in Figure 1.Hardware: Philips 7T Achieva system, 32 channel head array (Nova Medical), Field camera consisting of an array of 16 1H-based NMR field probes and a dedicated MR acquisition system(13).
GRE-Sequence: 0.7x0.7x2mm3 resolution, FOV=24x24x12cm3, 86shots, TE=20ms, TR=50ms, Total scan time=4.3s
Image reconstruction: Iterative 3D cg-SENSE reconstruction(10,14), multi-frequency-interpolation(15,16) for static off-resonance correction in each iteration, pre-monitored trajectories(17). Off-resonance and coil sensitivity maps from a 3D multi-echo, spin-warp pre-scan (6 echoes, TE 2-7 ms, 1.5x1.5x1.5mm3 resolution).
Post-processing: Removal of residual weighting by net array sensitivity using SPM12(18) (http://www.fil.ion.ucl.ac.uk/spm/software/spm12/). Removal of background phase using the STI Suite toolbox(19).
Results
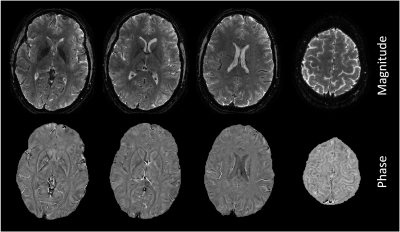
Figure 2 shows in-vivo results.Discussion
In this work, mono-planar T-Hex EPIs were introduced. The encoding concept is tailored to sampling per shot less k-space volume than one full k-space plane. Its main benefit in this regime is to gain flexibility when balancing readout and scan duration.The results of the in-vivo experiments corroborate the technical feasibility of the strategy. To achieve appealing image quality, image reconstruction was based on the expanded signal model described above. It proves to be well capable of dealing with long readouts. They come traditionally with challenges regarding eddy current effects on the field dynamics and, especially at high field, with respect to in-homogeneities of the static field. Those hurdles are here overcome here for the most part.
Just like its kindred T-Hex trajectories that sample more k-space volume than one k-space plane per shot(10), the encoding scheme provides a uniform undersampling and smooth T2* weighting. However, unlike them, it does not need time-consuming blips in the 2nd PE direction which sets it apart also from the approach presented in(20). Complementarily to multi-planar T-Hex trajectories, mono-planar T-Hex readouts are attractive in the high-resolution domain(21–23).
Compared to T-Hex spirals, T-Hex EPIs make, just like in 2D imaging, less efficient use of the gradient system and the available array encoding capabilities but offer more robustness against off-resonance artefacts. The lattice structure of the trajectory design might prove useful for future applications in two ways: First, the repetitiveness of the in-plane PE shifting for EPIs in the direction of the principal axis of the stack entails potential facilitation of trajectory calibration. As the repetitions of the first distinct set of EPIs differ only in the size of the prephaser gradient, this information might be exploited for the inference of field dynamics in a concurrently monitored experiment(21). Second, the fact that all tilting scenarios offered by T-Hex lead to the hexagonal grid being embedded in a finer rectangular grid, which is not tilted with respect to the stack's principal axis (Figure 1), may foster fast image reconstruction. Namely, mono-planar T-Hex EPI can be reconstructed on a FOV that is increased according to the T-Hex pattern using FFTs only instead of computationally expensive gridding operations. Alternatively, in this case, reconstruction may be performed using hexagonal FFTs(12,24). The image quality is in either case, however, limited by the accuracy of the applied gradient fields.
Acknowledgements
The authors thank Steffen Bollmann for his advice regarding the phase processing.References
1. Fernández‐Seara MA, Wang Z, Wang J, et al. Continuous arterial spin labeling perfusion measurements using single shot 3D GRASE at 3 T. Magn. Reson. Med. 2005;54:1241–1247 doi: 10.1002/mrm.20674.
2. Feinberg DA, Moeller S, Smith SM, et al. Multiplexed Echo Planar Imaging for Sub-Second Whole Brain FMRI and Fast Diffusion Imaging Valdes-Sosa PA, editor. PLoS ONE 2010;5:e15710 doi: 10.1371/journal.pone.0015710.
3. Borogovac A, Asllani I. Arterial Spin Labeling (ASL) fMRI: Advantages, Theoretical Constrains and Experimental Challenges in Neurosciences. International Journal of Biomedical Imaging. https://www.hindawi.com/journals/ijbi/2012/818456/. Published 2012. Accessed March 8, 2020 doi: https://doi.org/10.1155/2012/818456.
4. Vidorreta M, Wang Z, Rodríguez I, Pastor MA, Detre JA, Fernández-Seara MA. Comparison of 2D and 3D single-shot ASL perfusion fMRI sequences. NeuroImage 2013;0:662–671 doi: 10.1016/j.neuroimage.2012.10.087.
5. Balla DZ, Sanchez-Panchuelo RM, Wharton SJ, et al. Functional quantitative susceptibility mapping (fQSM). NeuroImage 2014;100:112–124 doi: 10.1016/j.neuroimage.2014.06.011.
6. Langkammer C, Bredies K, Poser BA, et al. Fast quantitative susceptibility mapping using 3D EPI and total generalized variation. NeuroImage 2015;111:622–630 doi: 10.1016/j.neuroimage.2015.02.041.
7. Özbay PS, Duerst Y, Wilm BJ, Pruessmann KP, Nanz D. Enhanced quantitative susceptibility mapping (QSM) using real-time field control. Magn. Reson. Med. 2018;79:770–778 doi: 10.1002/mrm.26735.
8. Poser BA, Koopmans PJ, Witzel T, Wald LL, Barth M. Three dimensional echo-planar imaging at 7 Tesla. NeuroImage 2010;51:261–266 doi: 10.1016/j.neuroimage.2010.01.108.
9. Engel M, Kasper L, Barmet C, et al. Single-shot spiral imaging at 7 T. Magn. Reson. Med. 2018;80:1836–1846 doi:10.1002/mrm.27176.
10. Engel M, Kasper L, Wilm B, et al. T-Hex: Tilted hexagonal grids for rapid 3D imaging. Magn. Reson. Med. n/a doi: https://doi.org/10.1002/mrm.28600.
11. Engel M, Kasper L, Patzig F, et al. Rapid whole-brain imaging with sub-mm resolution using sampling on tilted hexagonal grids (t-Hex). In: Proceedings of the 2020 ISMRM & SMRT virtual conference & exhibition. ; 2020. p. 3724.
12. Mersereau RM. The Processing of Hexagonally Sampled Two-Dimensional Signals. Proc. IEEE 1979;67:930–949.
13. Dietrich BE, Brunner DO, Wilm BJ, et al. A field camera for MR sequence monitoring and system analysis. Magn. Reson. Med. 2016;75:1831–1840 doi: 10.1002/mrm.25770.
14. Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn. Reson. Med. 2001;46:638–651 doi: 10.1002/mrm.1241.
15. Man L-C, Pauly JM, Macovski A. Multifrequency interpolation for fast off-resonance correction. Magn. Reson. Med. 1997;37:785–792 doi: 10.1002/mrm.1910370523.
16. Barmet C, Tsao J, Pruessmann KP. Sensitivity encoding and B0 inhomogeneity – A simultaneous reconstruction approach. In: Proceedings of the 13th Annual Meeting of ISMRM. Miami, Florida; 2005. p. 682.
17. Barmet C, Wilm BJ, Pavan M, et al. Concurrent higher-order field monitoring for routine head MRI: an integrated heteronuclear setup. In: Proceedings of the 18th Annual Meeting of ISMRM. Stockholm, Sweden; 2010. p. 216.
18. Stirnberg R, Stöcker T. Segmented K-space blipped-controlled aliasing in parallel imaging for high spatiotemporal resolution EPI. Magn. Reson. Med. 2021;85:1540–1551 doi: https://doi.org/10.1002/mrm.28486.
19. Kasper L, Engel M, Barmet C, et al. Rapid anatomical brain imaging using spiral acquisition and an expanded signal model. NeuroImage 2017 doi: 10.1016/j.neuroimage.2017.07.062.
20. Setsompop K, Fan Q, Stockmann J, et al. High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (gSlider-SMS): High-Resolution Diffusion Imaging with gSlider-SMS. Magn. Reson. Med. 2017 doi: 10.1002/mrm.26653.
21. Schwarz JM, Pracht ED, Stoecker T. GRAPPA Reconstructed 3D Wave-CAIPI TSE at 7 Tesla. In: Proceedings of the 27th Annual Meeting of ISMRM. Paris, France; 2018. p. 0938.
22. Rummelt NI. Array set addressing: Enabling efficient hexagonally sampled image processing. University of Florida; 2010.
Figures