0884
Variable Density Phase Encoding for High Resolution Single-Shot EPI
Mark Chiew1
1Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
1Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
Synopsis
A new variable density phase-encoding (vdPE) scheme for single-shot EPI is presented, in which phase encoding blips scale with a decaying exponential. This serves to reshape the signal decay envelope in the PE direction, resulting in shorter achievable TEs and reduced T2* blurring, without the need for partial Fourier sampling. We demonstrate this approach in high-resolution single-shot 2D EPI data, using a virtual-coil sensitivity encoded reconstruction, and show improved image fidelity and fewer artefacts compared to conventional EPI with ¾ partial Fourier. This approach could have utility for high-resolution, high-field brain imaging for applications such as layer-specific fMRI.
Introduction
High resolution single-shot gradient echo EPI can require long echo trains to adequately sample large matrix sizes, even with the use of parallel imaging. These long echo trains can limit the minimum achievable TE (time of k-space centre crossing), and are susceptible to T2* blurring effects1. As T2* decreases, these factors become more important, particularly when higher field strengths are being used to facilitate high resolution acquisitions by providing increased SNR. Furthermore, conventional high resolution EPI often relies on partial Fourier phase encoding to achieve desired TEs, at the cost of additional potential blurring incurred due to the reduced sampling window. As high resolution single-shot imaging at ultra-high field is becoming popular for applications such as layer-specific fMRI2, preserving spatial fidelity and specificity will also be increasingly important.Here, we propose an alternative phase-encoding scheme for single-shot EPI, which employs variable density phase encoding (vdPE) steps, which enables shorter TEs while retaining a full k-space sampling window, and reduced T2* blurring effects by modifying the signal decay envelope in the PE direction. In contrast to conventional phase-encoding steps, the vdPE approach scales ∆ky proportionally to an exponential decay. In this scheme, when the vdPE “decay” parameter matches the actual T2* of the measured data, the signal decay envelope is linear instead of exponential (Fig. 1). As larger steps are taken at the beginning of the readout, the k-space centre is reached sooner, resulting in lower achievable TEs.
Methods
In the proposed vdPE scheme, phase-encoding blips are scaled by a decaying exponential:$$k_{vdPE}\sim Ae^{-t/\alpha}+B$$
resulting in the envelope:
$$S(k_{vdPE})\sim e^{log((k-B)/A)/T2*}=((k-B)/A)^{\alpha/T2*}$$
which is linear in k when $$$\alpha$$$ = T2*. The factors A and B are defined to achieve a desired resolution (kmax) for a given echo train length (NPE). As $$$\alpha$$$ is changed, the envelope function $$$S(k_{vdPE})$$$ ranges from concave and nearly flat ($$$\alpha$$$ << T2*), to convex and exponential shaped ($$$\alpha$$$ >> T2*) (Fig. 2).
Data were acquired on a single subject at 7T (Siemens Magnetom) using a single-shot, 2D multi-slice gradient echo EPI acquisition with the following common parameters: TE = 30 ms, TR = 320 ms, 4 slices, 16 repetitions, 0.8x0.8x1.5 mm3 resolution with a 256x256 matrix size. Two different phase-encoding schemes with matched TE and readout durations were used:
[¾PF]: 3/4 partial Fourier, in-plane acceleration factor R=3, with 64 acquired PE lines
[vdPE]: vdPE with = 45 ms (chosen to match TE with ¾PF), 64 acquired PE lines
Image reconstruction was performed identically between both protocols in all cases, as a linear regularized least-squares virtual-coil (VC) SENSE reconstruction3:
$$x=||ESx-d||^{2}_{2}-\lambda||∇x||^{2}_{2}$$
where $$$E$$$ is the Fourier encoding operator with additional phase modulation derived from a separately acquired field-map to model off-resonance, $$$S$$$ are phase-modulated sensitivity maps (estimated via ESPIRiT4) and their conjugates, $$$x$$$ is the image estimate, and $$$d$$$ is the measured multi-channel k-space data with its conjugates. $$$∇x$$$ denotes the finite difference operator in the PE direction, and $$$\lambda$$$=1 was selected to produce the best ¾PF VC reconstruction, and used for all reconstructions. For the ¾PF protocol, reconstruction was also performed with zero-filling (without VC), for comparison.
Results
Figure 3 shows the impact of the point-spread function associated with different signal decay envelopes, on two sources representing structures like adjacent cortical layers. Considerable blurring and mixing of components is observed with the ¾PF envelope, whereas the vdPE shows significantly reduced component mixing in the real channel, whereas slightly more signal energy is distributed in the imaginary channel.Figure 4 shows mean reconstructed images of a single slice, across both protocols. The ¾PF zero-filled image shows characteristic blurring, which is significantly reduced using the phase constrained VC reconstruction in both datasets. The zoomed region in red highlights an example where ringing artefact is visible in the ¾PF data, but not present in the vdPE image. Furthermore, the VC-reconstructed ¾PF image, despite regularisation, shows more high-frequency artefacts (particularly in posterior regions). However, both VC-reconstructions do exhibit fringe-like artefacts in anterior regions, although they manifest quite differently in the ¾PF and vdPE data.
As the vdPE scheme has larger gaps in k-space sampling, noise amplification will typically be worse than uniform density sampling schemes. Figure 5 shows tSNR maps for the different reconstructions, in which the ¾PF zero-filled image shows the highest tSNR, whereas the VC reconstructions showed comparable tSNR in peripheral regions. The vdPE reconstruction, as expected, showed lowest tSNR in the centre of the brain.
Discussion
The proposed vdPE EPI sampling approach reshapes signal decay envelopes across single-shot EPI readout, resulting in lower TEs and reduced T2* blurring without requiring the use of partial Fourier. The scheme is simple, parameterised by a single parameter, and reconstruction is straightforward using conventional techniques. The variable density sampling exhibits image contrast and geometric distortions that are comparable to conventional EPI. While images acquired with vdPE do show reduced SNR centrally, this is balanced by reduced blurring and fewer apparent artefacts. This approach is demonstrated here in 2D single-shot EPI, but could also be applied to 3D methods such as EVI or 3D GRASE to reduce blurring in the second phase encode direction.Acknowledgements
MC is supported by the Royal Academy of Engineering (RF201617\16\23). The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z).References
- Haacke, E. M. ‘The Effects of Finite Sampling in Spin-Echo or Field-Echo Magnetic Resonance Imaging’. Magnetic Resonance in Medicine 4, no. 5 (1987): 407–21.
- Koopmans, Peter J., and Essa Yacoub. ‘Strategies and Prospects for Cortical Depth Dependent T2 and T2* Weighted BOLD FMRI Studies’. NeuroImage 197 (2019): 668–76.
- Blaimer, Martin, Marcel Gutberlet, Peter Kellman, Felix A Breuer, Herbert Köstler, and Mark A Griswold. ‘Virtual Coil Concept for Improved Parallel MRI Employing Conjugate Symmetric Signals.’ Magnetic Resonance in Medicine 61, no. 1 (2009): 93–102
- Uecker, M, P Lai, M J Murphy, P Virtue, M Elad, John M Pauly, S S Vasanawala, and M Lustig. ‘ESPIRiT - An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE Meets GRAPPA’. Magnetic Resonance in Medicine 71, no. 3 (2014): 990–1001.
Figures
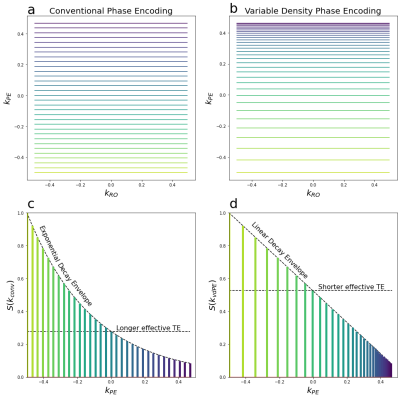
Figure 1 - (a) Conventional EPI phase encoding scheme showing uniform density coverage of k-space. (b) Proposed variable density EPI phase encoding, with larger PE blips at the beginning of the readout (yellow lines), and smaller blips towards the end (blue lines). (c) Conventional PE showing an exponential signal decay envelope. (d) Variable density PE with linear signal decay envelope ($$$\alpha$$$=T2*).
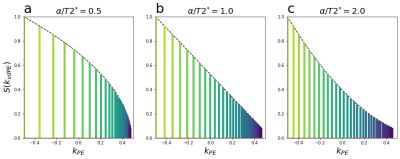
Figure 2 - (a) $$$\alpha$$$/T2* = 0.5, producing larger PE steps at the beginning of the readout, resulting in a shorter TE and a concave signal envelope. (b) $$$\alpha$$$/T2* = 1, as seen in Fig. 1, producing a linear signal envelope. (c) $$$\alpha$$$/T2* = 2.0, resulting in more uniform PE steps, a longer TE, approaching the expected exponential decay envelope for conventional sampling.
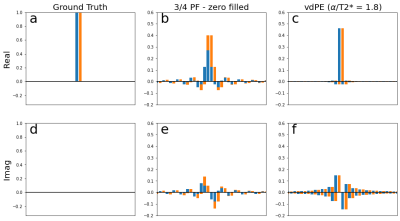
Figure 3 - Complex point spread functions showing the blurring effects of different sampling envelopes. (a,d) Two adjacent point sources (e.g. cortical layers) in blue and orange . (b,e) Blurring associated with a zero-filled, conventional phase-encoding readout, illustrating considerable mixing between components. (c,f) the vdPE readout shows considerably reduced blurring of components in the real-part, and slightly larger mixing in the imaginary part.
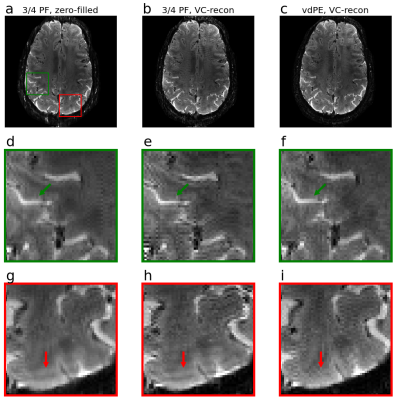
Figure 4 - Example reconstructions and zoomed insets. (a,d,g): Zero-filled reconstruction of the 3/4PF sampling, (b,e,h): VC reconstruction of the 3/4PF sampling, (c,f,i): VC reconstruction of the vdPE sampling. Green arrows denote a feature that is sharp in the VC reconstructions, and blurry in the zero-filled. Red arrows denote a ringing artefact visible in both 3/4PF data, but is not present in the vdPE reconstruction.
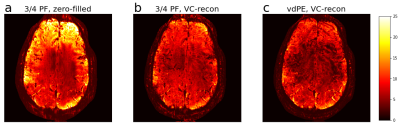
Figure 5 - tSNR maps. (a) 3/4PF, zero-filled, (b) 3/4PF, VC-reconstruction, (c) vdPE, VC-reconstruction.