0883
Boosting the SNR-efficiency of Free Gradient Waveform Diffusion MRI using Spiral Readouts and Ultra-Strong Gradients1CUBRIC, Cardiff University, Cardiff, United Kingdom, 2Image Sciences Institute, University Medical Center Utrecht, Utrecht, Netherlands, 3Siemens Healthcare Ltd, Camberly, United Kingdom, 4Siemens Healthcare GmbH, Erlangen, Germany, 5Mary McKillop Institute for Health Research, Faculty of Health Sciences, Australian Catholic University, Melbourne, Melbourne, Australia
Synopsis
Free gradient waveforms for diffusion MRI offer new insights in the underlying microstructure compared the classical Stejskal-Tanner linear encoding. A drawback of this approach is the prolonged echo time and thus decreased SNR. Here we present an approach to shorten the echo time by employing spiral readouts instead of echo-planar imaging and using the ultra-strong gradients of the Connectom scanner. The feasibility of this approach is demonstrated in a biomimetic phantom.
Introduction
An important goal pursued with diffusion MRI is the accurate characterization of the underlying tissue microstructure. Classical linear tensor encoding (LTE) is limited in its capabilities to do so as multiple microstructural configurations can give rise to the same signal and therefore degeneracies in the fitting1,2. These degeneracies can be resolved by incorporating additional diffusion gradient waveforms3,4,5 e.g. spherical tensor encoding (STE).Typically, free gradient waveforms need a longer echo time than pulsed-gradient LTE to reach reasonable diffusion weightings and thus lead to a lower SNR per unit b. This can be ameliorated by eliminating the part of the readout before the spin echo that is needed for echo-planar imaging, e.g. by switching to spiral readouts6,7,8. In combination with ultra-strong gradients (300 mT/m)9,10, this allows TE to be shortened considerably. In previous studies the spiral readout was only combined with LTE.
Here we present a free waveform diffusion sequence with spiral readouts and show first results in phantoms.
Methods
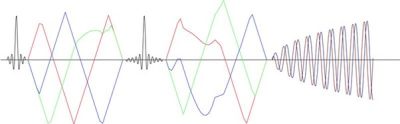
MR images were acquired on a Siemens Connectom Scanner (Siemens Healthcare GmbH, Erlangen, Germany) with a 300 mT/m maximum gradient amplitude. The sequence was developed in Siemens IDEA (starting with the MiniFlash), the programming platform for sequence development for Siemens scanners, and allows for the use of free gradient waveforms for diffusion encoding with a 2D spiral readout (Figure 1). The data were acquired with a 3 mm in-plane nominal resolution with a field of view of 210 mm and 3 times undersampling and constant k-space density.Diffusion encoding was achieved with two shells (b = [1, 2] ms/$$$\mu$$$m$$$ ^{2}$$$) and 30 directions for LTE and 3 directions for STE. The STE waveform was designed with the NOW toolbox11. The increased symmetry in timing of the diffusion gradients around the refocusing pulse gives higher possible b-values for concomitant field compensated waveforms. Those should be used to reduce artefacts12. To verify this, ten encodings were designed for two different settings with the same total encoding (46 ms) and pause time (6 ms) but different durations before and after the refocusing rf-pulse: 1. 23 and 17 ms, 2. 20 and 20 ms. The maximum gradient amplitude used was 220 mT/m and slew rate 60 T/m/s, which was lower than the hardware limits to minimise the chance of peripheral nerve stimulation and stay within the limits to avoid cardiac stimulation.
This acquisition gives a possible TE of 49 ms for STE with spiral readout, which was matched for LTE. This can be compared to the TE for an EPI readout of ~67 ms at similar imaging parameters. If the gradient amplitude is limited to 80 mT/m the TE for a spiral readout increases to ~70 ms and for an EPI to ~85 ms. Other imaging parameters were TR = 3.7 s, 15 slices with 2 mm thickness.
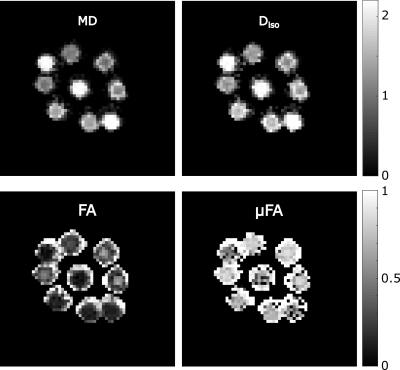
The k-space trajectory was measured with a field-camera (Skope Magnetic Resonance Technologies, Zurich, Switzerland), which was input to the expanded signal model reconstruction6. The reconstruction also included higher order extensions of k-space with terms up to third order spherical harmonics, concomitant fields and B0-inhomogeneities. The B0-map was calculated based on a fully sampled three echo gradient echo acquisition. STE and LTE images were combined to estimate mean diffusivity (MD), fractional anisotropy (FA), microscopic FA ($$$\mu$$$FA) and isotropic diffusion (Diso) in a biomimetic phantom13. The parameters were fitted in Matlab with self-written code and the help of the md-dmri toolbox14,15.
Results
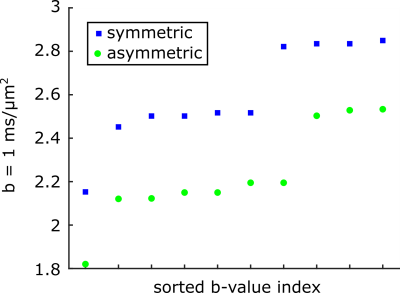
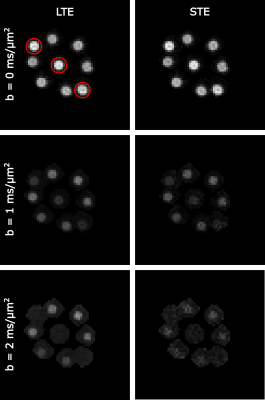
The b-values for the 10 STE waveforms with symmetric and asymmetric timing are shown in figure 3 in ascending order. There is an overlap in the b-value range that was achieved but the highest ones are consistently found for symmetric timing.Figure 3 shows the powder averaged signal for LTE and STE. A few vials only have water in the imaging slice and so the signal is gone for b=2 ms/$$$\mu$$$m$$$ ^{2}$$$).
The estimations for diffusion parameters are shown in figure 4. The values are in the expected range, except for the free water vials where the $$$\mu$$$FA is higher. The reason for this is that the signal is completely gone for the higher b-value.
Discussion
We demonstrate the feasibility of deriving microstructure measures, such as $$$\mu$$$FA and Diso, from free gradient waveform diffusion encodings with spiral readouts. The gain in echo time and SNR that was recently demonstrated8 can be translated to free gradient waveforms. The STE waveforms created with symmetric and asymmetric timing show a clear reduction in possible TE for a given b-value. For a constant encoding time, as used here, the TE is shorter for spirals since the readout starts with the spin echo in the k-space centre.Here we show the feasibility of estimating microstructure parameters with spiral readouts and free gradient waveform diffusion. In future work the results should be compared to the standard EPI readout.
When combined with multiple readouts, inversion-recovery, and slice-shuffling15, our approach can represent a very effective multimetric instrument to assess tissues microstructure by means of advanced multi-compartment models.
Acknowledgements
LM is supported by a Wellcome Trust Strategic Award (104943/Z/14/Z). CMWT is supported by a Sir Henry Wellcome Fellowship (215944/Z/19/Z) and a Veni grant (17331) from the Dutch Research Council (NWO). This work was supported by a Wellcome Trust Investigator Award (096646/Z/11/Z), a Wellcome Trust Strategic Award (104943/Z/14/Z), and an EPSRC equipment grant (EP/M029778/1) to DKJ. MM is supported by Siemens Healthcare Limited grant.
References
1 O. Jelescu, J. Veraart, E. Fieremans and D. S. Novikov, "Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue", NMR in Biomedicine, 29(1):33-47, 2016.
2 D. S. Novikov, J. Veraart, I. O. Jelescu and E. Fieremans, "Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI", NeuroImage, 174:518-538, 2018.
3 Lasič, S., Szczepankiewicz, F., Eriksson, S., Nilsson, M., Topgaard, D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics, 2:11, 2014.
4 Eriksson, S., Lasič, S., Nilsson, M., Westin, C. F., Topgaard, D. 2015. NMR diffusion-encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. The Journal of chemical physics, 142(10):104201, 2015.
5 Afzali, M., Tax, C. M., Chatziantoniou, C., & Jones, D. K. Comparison of different tensor encoding combinations in microstructural parameter estimation. In 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019):1471-1474. IEEE, 2019.
6 Wilm, B. J., Barmet, C., Gross, S., Kasper, L., Vannesjo, S. J., Haeberlin, M., ... & Pruessmann, K. P. Single‐shot spiral imaging enabled by an expanded encoding model: D emonstration in diffusion MRI. Magnetic resonance in medicine, 77(1):83-91, 2017.
7 Wilm, B. J., Hennel, F., Roesler, M. B., Weiger, M., & Pruessmann, K. P. Minimizing the echo time in diffusion imaging using spiral readouts and a head gradient system. Magnetic Resonance in Medicine, 84(6):3117-3127, 2020.
8 Lee, Y., Wilm, B. J., Brunner, D. O., Gross, S., Schmid, T., Nagy, Z., & Pruessmann, K. P. On the signal‐to‐noise ratio benefit of spiral acquisition in diffusion MRI. Magnetic Resonance in Medicine, 2020 (online preprint).
9 Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, and Wald LL. Pushing the limits of in vivo diffusion MRI for the human connectome project. NeuroImage, 80:220-233, 2013.
10 Jones, D. K., Alexander, D. C., Bowtell, R., Cercignani, M., Dell'Acqua, F., McHugh, D. J., ... & Tax, C. M. Microstructural imaging of the human brain with a ‘super-scanner’: 10 key advantages of ultra-strong gradients for diffusion MRI. NeuroImage, 182:8-38, 2013.
11 Sjölund, J., Szczepankiewicz, F., Nilsson, M., Topgaard, D., Westin, C. F., & Knutsson, H Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of magnetic resonance, 261:157-168, 2013.
12 Szczepankiewicz F, Westin CF, Nilsson M. Maxwell-compensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding. Magn Reson Med. 82(4):1424-1437, 2013.
13 Hubbard, P. L., Zhou, F. L., Eichhorn, S. J., & Parker, G. J. Biomimetic phantom for the validation of diffusion magnetic resonance imaging. Magnetic resonance in medicine, 73(1):299-305, 2015.
14 Markus Nilsson, Filip Szczepankiewicz, Björn Lampinen, André Ahlgren, João P. de Almeida Martins, Samo Lasic, Carl-Fredrik Westin, and Daniel Topgaard. An open-source framework for analysis of multidimensional diffusion MRI data implemented in MATLAB. Proc. Intl. Soc. Mag. Reson. Med. (26), Paris, France, 2018
15 Hutter, J., Slator, P. J., Christiaens, D., Teixeira, R. P. A., Roberts, T., Jackson, L., ... & Hajnal, J. V. Integrated and efficient diffusion-relaxometry using ZEBRA. Scientific reports, 8(1):1-13, 2018.
Figures