0882

Optimizing the fixed angular increment between k-space spokes can lead to improved SNR in radial imaging

S Sophie Schauman¹, Thomas W Okell¹, and Mark Chiew¹
¹Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom

Synopsis

Many dynamic MRI methods use golden ratio radial sampling. Here, we show that golden ratio sampling is not always ideal from an SNR point of view, and that optimizing the fixed angular increment between spokes can lead to more uniform coverage of k-space, which in turn can lead to lower g-factors in a non-Cartesian parallel imaging reconstruction. The method we present, the Set Increment with Limited Views Encoding Ratio method, SILVER, maintains the flexibility of reconstructing a single dataset at multiple temporal resolutions but improves SNR compared with the golden ratio method.

Introduction

Dynamic and fast MRI methods often use radial sampling because of its robustness to motion and noiselike undersampling artefacts[1]. A particularly common sampling approach is the golden ratio method (GR[2]), which allows for reconstruction at multiple temporal resolutions since approximately uniform coverage of k-space is achieved for any number of consecutively sampled spokes. This method provides great flexibility but is not as SNR-optimal as radial sampling with equidistant spokes because of the non-uniform coverage of k-space[3]. Here, we present a method (The Set Increment with Limited Views Encoding Ratio, SILVER) that retains the simplicity and flexibility of GR sampling but improves the uniformity of the sampling and thus SNR.

Methods

The golden angle increment leads to reasonable sampling uniformity for any numbers of spokes, and peak uniformity at numbers of spokes corresponding to Fibonacci numbers. Because data is often only reconstructed at a small number of temporal resolutions, a more optimal angular increment between spokes can be found by optimising the radial trajectory for uniformity only over a restricted set of reconstruction windows (spokes/frame). This trades off the complete flexibility of the GR increment for improved uniformity, while retaining enough flexibility to encompass a small number of different target window sizes.

The optimisation was set up to maximise the minimum sampling efficiency for a set of window sizes:
$$cost=\max_\alpha(\min_{N{\in}S}(U(\alpha,N)/U_{ref}(N)))$$
S is the set of window sizes that is optimised for, U is the uniformity that is achieved with a fixed angular increment $$$\alpha$$$ and N spokes. U_ref is the uniformity calculated for radially uniform sampling ($$$\alpha=1/N$$$).

The inverse of the sum of Cartesian distances from all spoke tips to each other was used as a uniformity metric, known as the electrostatic potential metric, EP.

The source code is available on https://github.com/SophieSchau/SILVER.

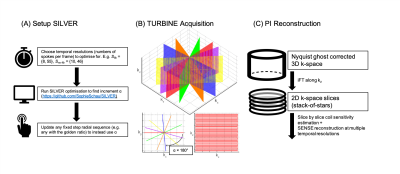
SILVER was used to optimize radial sampling for two sets of window sizes (navigator and imaging), S_fib = {8, 55}, and S_no-fib = {10,46}. S_fib corresponds to numbers in the Fibonacci sequence. S_no-fib is non-optimal for GR. 3T scans of a bottle phantom and one healthy volunteer were acquired using a 3D radial-Cartesian acquisition where each shot was a rotated Cartesian EPI blade (TURBINE[4], TR=50ms, TE=28ms, FA=15°). Data were reconstructed using an iterative SENSE reconstruction in MATLAB. Imaging resolution was set to 2mm², and the navigator data were downsampled to a resolution of 6.7mm². Coil sensitivity maps were generated from the temporal mean and estimated using the adaptive combine method[5]. Data acquisition and reconstruction is summarized in Figure 1.

Because the simple uniformity metrics do not take into account the effect of noise amplification due to parallel imaging and how the trajectory and the coil sensitivity profiles interact, g-factor maps were calculated using Monte Carlo simulations. Average g-factor maps were then generated by taking the root-mean-square across frames.

Results

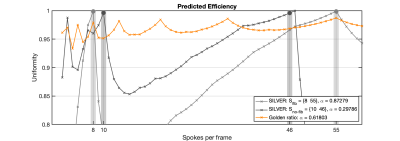
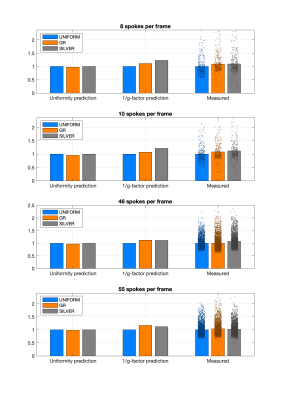
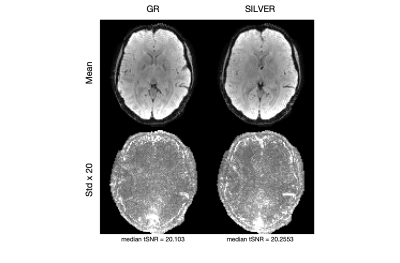
Figure 2 shows that when optimised for two temporal resolutions, SILVER is expected to produce better uniformity than GR both for S_fib and S_no-fib.

Predicted g-factor noise amplification for the various trajectories corresponded well with the empirical SNR. For 10 spokes/frame, SILVER produced 3.5% higher SNR than GR, and 12% higher than Uniform spokes (Figure 3).

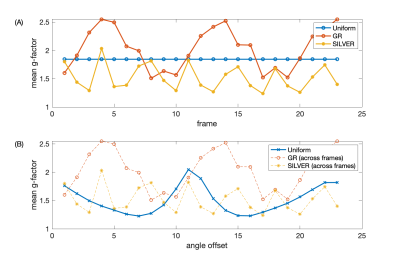
Figure 4(A) shows the mean g-factor frame by frame. For uniform sampling it is constant, GR and SILVER show oscillatory behaviour as the trajectory rotation interacts with the coil sensitivities. Figure 4(B) shows that if a range of starting angles are sampled, uniform sampling has lower g-factors on average, but without prior knowledge of the coil sensitivities it is impossible to optimise uniform sampling for the optimal starting angle.

In-vivo images acquired with GR, SILVER, and uniformly distributed spokes are shown in Figure 5 (55 spokes per frame). The stronger noise amplification in GR is highlighted using the red arrows.

Discussion

The SILVER method is a simple, single parameter optimisation that results in small improvements in uniformity compared to GR when a limited number of window sizes are targeted. The small improvement in uniformity results in larger improvements in reduced noise amplification in PI reconstruction. The results showed SILVER performing better than both GR and uniform sampling. The reason SILVER outperformed uniform sampling is because the trajectory is rotated frame by frame and thus achieves its average performance overall whereas uniform sampling has a fixed rotation (which might be better or worse than its average performance). Acquiring rotated trajectories in different frames can also be beneficial for temporally regularised reconstructions.

SILVER can be useful for generating multi-temporal resolution data e.g. for multi-shot self-navigation. SILVER could also be used in dynamic imaging where binning is performed retrospectively, and the number of spokes in each bin is unknown at the time of acquisition as long as a range of possible window sizes are optimized for. It could thus be useful in a range of dynamic imaging methods, eg. dynamic speech imaging[6], cardiac imaging[7], fMRI[4], and cerebral blood flow imaging[8].

Conclusion

We have shown that we can do better than GR when radial data is reconstructed at a limited number of window sizes. Even without knowledge of coil sensitivities, lower g-factors can be reached by optimizing for uniformity alone, thus showing the applicability of this simple optimization approach.

Acknowledgements

The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z).

SS was supported by funding from the Engineering and Physical Sciences Research Council (EPSRC) and Medical Research Council (MRC) (EP/L016052/1).

MC was supported by funding from the Royal Academy of Engineering (RF201617\16\23).

TO was supported by funding from the Wellcome Trust (Sir Henry Dale Fellowship).

References

1. Rasche V, Boer RWD, Holz D, Proksa R. Continuous radial data acquisition for dynamic MRI. Magn. Reson. Med. 1995;34:754–761 doi: 10.1002/mrm.1910340515.

2. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An Optimal Radial Profile Order Based on the Golden Ratio for Time-Resolved MRI. IEEE Trans. Med. Imaging 2007;26:68–76 doi: 10.1109/TMI.2006.885337.

3. Tsai C-M, Nishimura DG. Reduced aliasing artifacts using variable-density k-space sampling trajectories. Magn. Reson. Med. 2000;43:452–458 doi: 10.1002/(SICI)1522-2594(200003)43:3<452::AID-MRM18>3.0.CO;2-B.

4. Graedel NN, McNab JA, Chiew M, Miller KL. Motion correction for functional MRI with three-dimensional hybrid radial-Cartesian EPI: Motion Correction for TURBINE fMRI. Magn. Reson. Med. 2017;78:527–540 doi: 10.1002/mrm.26390.

5. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn. Reson. Med. 2000;43:682–690 doi: 10.1002/(SICI)1522-2594(200005)43:5<682::AID-MRM10>3.0.CO;2-G.

6. Kim Y-C, Narayanan SS, Nayak KS. Flexible retrospective selection of temporal resolution in real-time speech MRI using a golden-ratio spiral view order: Speech MRI using Golden-Ratio Spiral. Magn. Reson. Med. 2011;65:1365–1371 doi: 10.1002/mrm.22714.

7. Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing: XD-GRASP: Extra-Dimensional Golden-angle Radial Sparse Parallel MRI. Magn. Reson. Med. 2016;75:775–788 doi: 10.1002/mrm.25665.

8. Okell TW. Combined angiography and perfusion using radial imaging and arterial spin labeling. Magn. Reson. Med 2019;81:182–194 doi: 10.1002/mrm.27366.

Figures

Fig 1 - SILVER optimizes a single parameter, the angular increment, α, in the window sizes that are included in the optimisation set, S (A). In this project a TURBINE acquisition scheme, (B), was used (fig modified from [4]), and the data were reconstructed using 2D non-Cartesian SENSE (C).

Fig 2 - Predicted sampling efficiency for different numbers of spokes per frame. SILVER optimised regions highlighted in gray.

Fig 3 - The leftmost group shows the predicted efficiency for each trajectory using the EP metric. The middle group shows the prediction when including the coils used in the experiment. The rightmost group shows the measured data. The bars show means, and the scatter plot shows the SNR in individual pixels. All groups are normalised to the mean of the uniform sampling pattern.

Fig 4 - (A) shows the frame-wise g-factor for 8 spokes/frame using the different trajectories. (B) shows GR and SILVER from (A) in dashed thin lines for reference, but the focus is on showing that varying the starting angle of uniform sampling has a similar effect to that of GR and SILVER, but its average g-factor is lower than both GR and SILVER.

Fig 5 - In vivo comparison of SILVER and GR at 55 spokes per frame. Since it is a Fibonacci number, GR is optimal and the difference is small but still measurable in the tSNR. The top row shows the temporal average image. The bottom row shows the standard deviation across the frames.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0882