Introduction

Non-Cartesian MRI acquisitions, such as radial or spiral acquisitions, have several advantages. They are more robust to motion artifacts than Cartesian sampling because they oversample the center of k-space with each acquisition. Furthermore, they provide real-time reconstructions enabling retrospective motion correction or gating¹. Hence, they are promising for imaging fetuses, neonates, and non-cooperative subjects.

Traditionally, these acquisitions involve performing successive readout trajectories at regularly incremented angles, such as by the golden angle². However, one drawback with this implementation is the occurrence of clustering of readout trajectories after data is sorted into cardiac phases for CINE reconstruction. At certain combinations of acquisition repetition times (TRs) and heart rates (HRs), closely spaced trajectories are binned into the same cardiac phase resulting in coherent aliasing artifacts that degrade image quality. These artifacts become highly problematic when using accelerated imaging with reconstruction techniques such as compressed sensing³.

Here, we propose a technique to reduce trajectory clustering after gating is applied while also allowing uniform sampling for real-time reconstructions. It involves playing additional angles between blocks of traditional readouts. These angles are then optimized to minimize clustering artifacts for a given protocol.

Methods

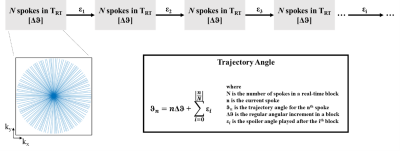
Design Constraints: Two design constraints must be addressed. Firstly, for the duration of a real-time image frame (T_RT), trajectories must cover k-space in a quasi-uniform distribution. Secondly, after cardiac gating, the trajectories must be resorted into cardiac phases with minimal clustering. To achieve this, trajectories are incremented with a constant angle (Δθ) over a block of duration T_RT. After each block, an additional angle (Ɛ_i after i^th block) is applied once to disrupt the pattern (Figure 1).

Appropriate values for Ɛ may be determined through numerical simulation, by finding a set of Ɛ that minimizes a metric for trajectory clustering over a physiological range of constant HRs. The metric chosen for this work is the standard deviation of trajectory angular differences (S). For example, uniform radial sampling of k-space has S being 0. In the presence of clustering, a skewed distribution of trajectory angular differences arises, and as clustering increases, S increases.

The loss function is calculated over a range of typical HRs and then summed over all HRs to give a global loss. The optimal Ɛ is then obtained by minimizing the global loss function:
$$ \min_{Ɛ}{\sum_{rr}{\sigma(R_{rr,c}(K(Ɛ))}}$$
where σ is the standard deviation operator, R_rr,c is the operator sorting the trajectories into c cardiac phases based on heart rate rr, and K is the calculated trajectory angles based on Ɛ. Particle swarm optimization (PSO) is used to minimize S as the landscape of the loss function is non-smooth and non-convex⁴. The PSO comprises 40 particles which are initially at random Ɛ values and iteratively converge towards a global minimum.

Optimization: This technique to reduce clustering is demonstrated in the use of radial acquisitions in fetal cardiac MRI through three simulations. In each simulation, radial trajectories were simulated with TR = 6.6 ms, T_RT = 422.4 ms, scan duration = 10 s, and in each block Δθ = golden angle. The CINE comprised 15 cardiac phases. The simulations differed only by the value of Ɛ: (1) traditional scanning: Ɛ = 0, (2) random: Ɛ ~ randomly distributed between 0 and 2π [performed 10 times], and (3) optimal: Ɛ optimized with the PSO above. The behaviors of the different sets of Ɛ were also analyzed using the entropy of the resulting point spread function (PSF). Representative reconstructions with compressed sensing were performed using each set of Ɛ to demonstrate reduction of artifacts.

Results

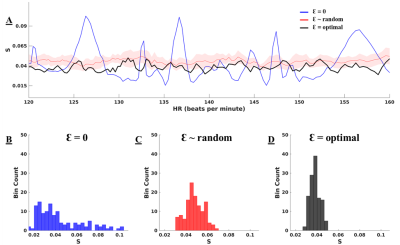
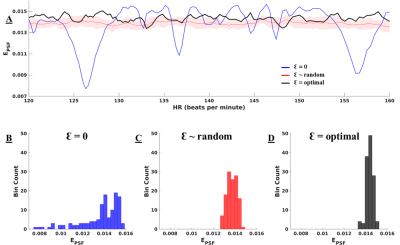
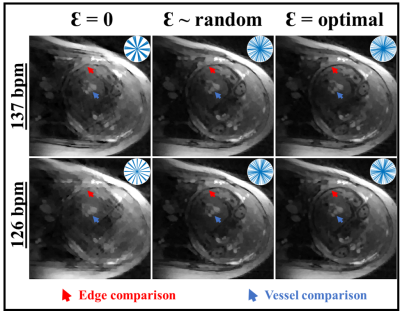
Figure 2A displays the values of S for each pattern of Ɛ, across a physiological range of fetal HRs. With Ɛ = 0 (blue line), peaks in S are evident at specific HRs, corresponding to high clustering in k-space. Conversely, these peaks are suppressed when using random (red) and optimal (black) Ɛ with reduced variability in S as in Figure 2B-D. The optimal set of Ɛ leads to the best overall reduction in S. Figure 3A displays the entropy of the PSF versus HR for the three sets of Ɛ with their histograms in Figure 3B-D. The optimized Ɛ has a consistently high entropy with low variation, denoting more incoherence in sampling. Figure 4 shows representative reconstructions in simulated k-space from a fetal slice showing the 3-vessel view. With Ɛ = 0, the reconstruction contains streaking artifacts that make the anatomy less conspicuous. With random Ɛ, there is visual improvement in the reconstruction. With optimal Ɛ, there is further improvement with some edges, such as the fetal surface, becoming less blurred.

Discussion

The method proposed here allows for a more incoherent k-space for CINE reconstructions and windows of acquisitions to be reconstructed into real-time series. While the optimization is performed over constant fetal HRs, variations in HR naturally improve incoherence in CINEs. Since optimization of Ɛ must be performed for a set of typical HRs for a given protocol setting (for instance, number of readouts or TR), random Ɛ provides a good alternative to minimize clustering for imaging requiring in-scan changes.

Conclusion

We have proposed and demonstrated a novel sampling pipeline to minimize coherence in non-Cartesian k-space.

Acknowledgements

No acknowledgement found.