0859

A generic framework for real-time 3D motion estimation from highly undersampled k-space using deep learning

Maarten Terpstra^1,2, Matteo Maspero^1,2, Tom Bruijnen^1,2, Joost Verhoeff¹, Jan Lagendijk¹, and Cornelis A.T. van den Berg^1,2
¹Department of Radiotherapy, University Medical Center Utrecht, Utrecht, Netherlands, ²Computational Imaging Group for MR diagnostics & therapy, University Medical Center Utrecht, Utrecht, Netherlands

Synopsis

Motion estimation from MRI is important for image-guided radiotherapy. Specifically, for online adaptive MR-guided radiotherapy, the motion fields need to be available with high temporal resolution and a low latency. To achieve the required speed, MR acquisition is generally heavily accelerated, which results in image artifacts. Previously we have presented a deep learning method for real-time motion estimation in 2D that is able to resolve image artifacts. Here, we extend this method to 3D by training on prospectively undersampled respiratory-resolved data showing that our method produces high-quality motion fields at R=30 and even generalizes to CT without retraining.

Introduction

Motion estimation from MRI is important for radiotherapy¹. In particular, for online adaptive MRI-guided radiotherapy (MRgRT) motion estimation is necessary to achieve a highly conformal irradiation of the target, sparing organs-at-risk². For this application, it is crucial that volumetric images are readily available with high temporal resolution. As 3D MR acquisition is time-consuming, it must be highly accelerated e.g., with undersampling; however, undersampling introduces image artifacts which hinders accurate motion estimation. Previously, we showed that a two-step approach where non-uniform Fourier reconstruction followed by a deep learning (DL) motion estimation model is able to resolve motion despite image artifacts, enabling real-time motion estimation from highly-undersampled 2D MRI³. In this work, we extend the 2D DL-based approach to perform real-time 3D motion estimation.

Materials and Methods

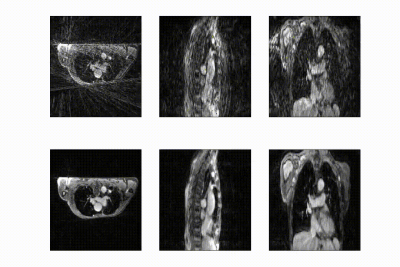
Free-breathing fat-suppressed golden-angle radial stack-of-stars (GA-SOS) T1-w GRE MRI of the thorax were acquired for 7.3 min in 27 patients with lung cancer on a 1.5T MRI (MR-RT Philips Healthcare) at 2.2x2.2x3.5mm³ with a FOV of 350x350x270mm³ during Gadolinium injection. As ground-truth time-resolved 3D motion is very hard to obtain, we employed respiratory-resolved four-dimensional image reconstruction as a surrogate for time-resolved data. K-space was retrospectively sorted into 20 respiratory phases (R~7) and reconstructed using the non-uniform Fourier transform⁴ (NUFFT). Ground-truth DVFs were obtained by computing optical flow⁵ (OF) on the NUFFT-reconstructed respiratory-resolved reconstructions to exhale, inhale, and midvent positions. These respiratory-resolved images were used to train a multi-resolution 3D convolution neural network (CNN) to learn deformation vector fields (DVFs).

The network hyperparamaters were found using a gridsearch, resulting in an optimal model with 3 CNNs operating at different resolutions; 4x-downsampled, 2x-downsampled, and full resolution, respectively. The data generation procedure and model output is shown in in Figure 1.
The model was trained by minimizing \(\mathcal{L}=\alpha\cdot(\mathcal{L}_{\text{mag}}+\mathcal{L}_{\phi})+(1-\alpha)\cdot\mathcal{L}_{\text{EPE}}+\lambda\cdot\nabla\text{DVF}\), where \(\mathcal{L}_{\text{mag}}\) is the \(\ell_2\)-norm of the magnitude difference between the target and output DVF, \(\mathcal{L}_\phi\) is the \(\ell_2\)-norm of the difference in angle between the target and output DVF, \(\mathcal{L}_{\text{EPE}}\) is the end-point-error i.e., the \(\ell_2\)-norm of the difference of the output DVF and target DVF, and \(\nabla\text{DVF}\) enforces smoothness of the DVF by penalizing the second derivative.
Based on the gridsearch results, we found \(\alpha=0.8\) and \(\lambda=10^{-5}\) to be good hyperparameters.
The network was trained end-to-end, i.e. we performed backpropagation during training over all levels, using Adam⁶ (lr=10^-4, 10^-3 L2 weight decay). The learning rate was halved when the test-EPE did not decrease with 10^-8. In total, the model was trained with 17 patients, comprising of 2108 volume pairs, and validated and tested on 5 patients, comprising of 620 volume pairs.The model was evaluated on the EPE (\(\mu\pm\sigma\)) calculated within the body anatomy on the following datasets:

Test set of 5 respiratory-resolved patients. The test set was NUFFT-reconstructed with higher acceleration as applied during training, going up to 100 respiratory phases i.e. R~32. DVFs generated by our model were compared to optical flow computed on compressed sense reconstructions⁷with total variation in time.
On the digital XCAT phantom⁸. Respiratory motion up to 50mm in the anterior-posterior direction and 100mm in the feet-head direction were simulated, providing ground-truth DVFs. Retrospective undersampling using a GA-SOS readout was performed up to R=50.
Fully-sampled CT Data. To test the generalization ability, we evaluated a publicly accessible 4D-CT dataset⁹ with respiratory motion in the intrathoracic region using optical flow DVFs without retraining the model.

Results and discussion

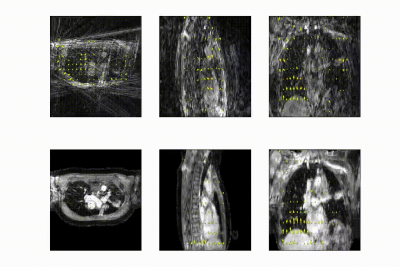
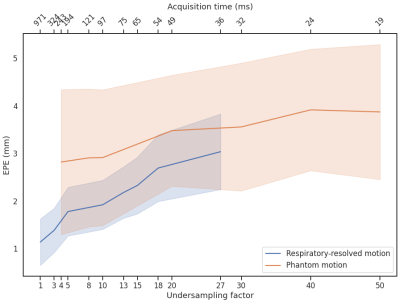
The full model was trained in ~24h. After training, inference of the model with a full 3D reference/dynamic volume-pair of 206x206x77 voxels takes 30 ms on a NVIDIA V100 GPU.

The DVFs produced by our model show good agreement with the motion present in the images producing a mean EPE of 2.3±0.6mm at R~10 (Figure 2) and 2.5±0.4mm at R~18 (Figure 3). Quantitative evaluation of our model up to 100 respiratory phases (R~27) show that the mean EPE<3mm. However, the ground-truth compressed sense DVFs may also contain errors due to the high undersampling factors used and because of time-regularization. These results are consistent with the results on the digital phantom (Figure 4), which demonstrated that at 30-fold retrospective undersampling the EPE is ~3mm.

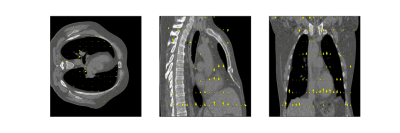
Evaluation on the 4D-CT dataset shows excellent correlation of the estimated motion with the motion in the images, even though the model was trained on MR images (Figure 5). Compared to the OF DVF, we achieve a mean EPE of 0.95±0.5 mm, with a maximum mean EPE of 1.6 mm.

To our knowledge, this is the first 3D DL-based motion estimation method from highly undersampled images. Our method is accurate and significantly faster with an inference time of 30 ms versus 400-9000 ms for comparable methods^10,11,12. Our model currently exploits spatial information, without considering temporal information. In the future, we plan to further evaluate the model using physical phantoms and validate time-resolved motion estimation performance.

Conclusion

Our approach estimates motion from heavily undersampled images in 3D with high accuracy in 30 ms. It was trained on respiratory-resolved images to perform time-resolved motion estimation. We have shown that our approach is accurate, fast, and generalizes to higher acceleration factors and even other imaging modalities.

Acknowledgements

This work is part of the research programme HTSM with project number 15354, which is (partly) financed by the Netherlands Organisation for Scientific Research (NWO) and Philips Healthcare. We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Quadro RTX 5000 GPU used for prototyping this research.

References

[1] Keall et al. "The management of respiratory motion in radiation oncology report of AAPM Task Group 76a". Med. Phys., 33: 3874-3900. (2006)

[2] Keall et al. "See, think, and act: real-time adaptive radiotherapy." Sem. Rad. Onc. 29.3 2019.

[3] Terpstra et al. "Deep learning-based image reconstruction and motion estimation from undersampled radial k-space for real-time MRI-guided radiotherapy." PMB (2020).

[4] Fessler and Sutton. "Nonuniform fast Fourier transforms using min-max interpolation." IEEE transactions on signal processing 51.2 (2003)

[5] Zachiu et al. "An improved optical flow tracking technique for real-time MR-guided beam therapies in moving organs." PMB 60.23 (2015)

[6] Kingma et al. "Adam: A method for stochastic optimization." arXiv preprint arXiv:1412.6980 (2014).

[7] Lustig et al. "Sparse MRI: The application of compressed sensing for rapid MR imaging." MRM 58.6 (2007)

[8] Segars et al. "4D XCAT phantom for multimodality imaging research." Medical physics 37.9 (2010)

[9] Vandemeulebroucke et al. "The POPI-model, a point-validated pixel-based breathing thorax model." ICCR. Vol. 2. 2007.

[10] Eppenhof et al. Fast contour propagation for MR-guided prostate radiotherapy using CNNs. Proc. ESTRO (2020).

[11] Stemkens et al. Image-driven, model-based 3D abdominal motion estimation for MR-guided radiotherapy PMB. Vol. 61. 2016

[12] Morales et al. "Implementation and validation of a three-dimensional cardiac motion estimation network." Radiology: Artificial Intelligence 1.4 (2019).

Figures

Figure 1: Schematic of 4D reconstruction and multi-level motion estimation. Long radial acquisitions (7.3 min.) with motion mixing are respiratory-binned and reconstructed to three spatial resolutions by cropping k-space around k₀. These images serve as training data for our multi-resolution motion model -- together with optical flow to inhale, exhale, and midvent positions -- to learn a three-dimensional deformation vector field. The lowest resolution CNN has 3x3x3 3D convolutional filters, the middle CNN has 5x5x5 filters, and the final CNN again uses 3x3x3 filters.

Figure 2: Typical motion reconstruction at R~10. The computed DVFs were computed using NUFFT-reconstructed respiratory-resolved images with 30 respiratory phases (top row, R~10), while the bottom row shows optical flow computed on compressed sense reconstructions. Compared to these DVFs, our model achieves a mean EPE of \(2.29\pm0.57\) mm despite significant artifacts. However, some motion artifacts remain at the anterior side due to undersampling artifacts.

Figure 3: Typical motion reconstruction at R~18. The computed DVFs were computed using NUFFTreconstructed respiratory-resolved images with 70 respiratory phases (top row, R~18), while the bottom row shows optical flow computed on compressed sense reconstructions. Compared to these DVFs, our model achieves a mean EPE of \(2.48\pm0.42\) mm compared to compressed sense optical flow. However, some motion artifacts remain at the anterior side due to undersampling artifacts.

Figure 4: Quantitative results. The end-point-error as a function of the undersampling factor for the respiratory-resolved data (blue), as well as the phantom data (orange). The mean EPE (solid line, with standard deviation as shaded area) compared to ground-truth optical flow remains within 3mm for the respiratory-resolved data. For the phantom data, the error is slightly higher due to the large motion amplitude, but increases slowly as the undersampling factor increases. The top axis shows the acquisition time per slice (ms) at that undersampling factor.

Figure 5: 4D-CT evaluation. Evaluation of our model trained on MRI on 4D CT data without retraining. The mean error was 0.95mm, which is slightly smaller than the voxel size of 0.97 x 0.97 x 2 mm. The maximum mean error was 1.6 mm.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0859