Introduction

A major drawback of MRSI is long acquisition times for 4D (k,t) spatio-temporal space, resulting in critical need for high acceleration strategies. This is particularly relevant for high-resolution whole-brain MRSI where traditional acquisition schemes require several hours. Acceleration can be performed by parallel imaging such as SENSE and GRAPPA with uniform undersampling, or by Compressed-Sensing (CS) with random undersampling, but these techniques generally don’t allow acceleration factors (AF) above 10^1,2. Spatial-spectral encoding (SSE) techniques enable higher AF of 10-100³, but current SSE trajectories require temporal interleaves at ultra-high field to reach a broad spectral bandwidth and high spatial resolution. However, temporal interleaving creates spectral sidebands that reduce SNR and overlap with metabolite signals. Thus, it should be avoided³. Circular waveforms are characterized by absence of deadtime for repeated rewinding, and have constant and moderate gradient slewrate not demanding for gradient hardware. We introduce ECCENTRIC, a novel SSE trajectory following a random pattern of off-center circles weighted with a highly desired 1/|k| density function particularly suitable for sparse undersampling acceleration to prevent coherent aliasing artefacts. With this approach the circle size can be chosen to prevent the use of temporal interleaving independently of the spatial resolution.

Methods:

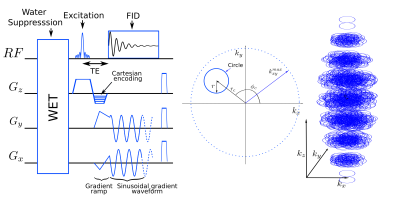
ECCENTRIC Trajectory
The 3D k-space is divided into k_x-k_y planes where off-center circles are measured, while k_z is encoded by Cartesian phase-encoding. The number of eccentric circles necessary to achieve full sampling of k_x-k_y planes is derived from rosette trajectory that needs $$$n\pi$$$ circles with $$$n$$$ being the matrix size.⁴ The number of circles of radius $$$r$$$ for full sampling is given by $$$n\pi\frac{k_{xy}^{max}}{2r}$$$ with $$$k_{xy}^{max}$$$ the largest in-plane k-space absolute value(FIG.1). To achieve spherical 3D k-space coverage, $$$k_{xy}^{max}$$$ is decreased along the 3rd dimension following $$$k_{xy}^{max}=\frac{n}{2FoV}\sqrt{1-k_z/k_z^{max}}$$$. A short constant-time gradient ramp is used to reach initial off-center $$$k_{xy}$$$ position and velocity, which is applied simultaneously with the excitation rewinder and phase encoding (Fig.1). Circle center positions, parametrized by polar coordinates $$$(r_c,\phi_c)$$$ (FIG.1), are chosen randomly and differently for each plane with $$$r_c$$$ in $$$[0,max(k_{xy}^{max}-r,r)]$$$ and $$$\phi_c$$$ in $$$[0,2\pi]$$$. The homogeneous distribution in polar coordinates results in $$$1/|k|$$$ weighting in the Cartesian k-space. Spatial response function⁵ (SRF) was computed on a 64x64 matrix using a NUFFT reconstruction⁶ for ECCENTRIC, rosette and concentric circle trajectories.
Sequence and acquisition parameters
The ECCENTRIC was implemented on a 7T scanner (Terra/Siemens/Erlangen/Germany) with a NOVA head coil (32Rx/8Tx) and appended to a FID-MRSI sequence⁷ with 0.9ms echo-time (TE), 35° excitation flip-angle, 450ms repetition-time (TR) and WET water suppression. The Field-of-View (FoV) was set to (A/P-R/L-H/F) 220x220x45mm³ with 35mm-thick excited slab. The spatial resolution was 64x64x9 resulting in 3.4x3.4x5mm³ voxels. The ECCENTRIC circle radius was set to $$$r=\frac{64}{2FoV}$$$ (half the rosette circle radius), the spectral bandwidth set to 2326Hz didn’t require temporal interleaving, and the FID was sampled for 350ms. The resulting acquisition time of fully sampled data was 8min.
Reconstruction and metabolite quantification
The non-Cartesian MRSI signal was reconstructed using the Total-Generalized-Variation (TGV) constrained low-rank model^9,10,11 allowing for reconstruction of randomly undersampled k-space. Assuming that the magnetization in image space $$$\rho(\mathbf{r},t)$$$, can be separated into several spatial and temporal components$$\rho(\mathbf{r},t)=\sum_{n=1}^{K}U_n(\mathbf{r})V_n(t),$$these components are retrieved by the minimization problem$$\arg\min_{\mathbf{U}\mathbf{V}}\left\|\mathbf{s}-\mathcal{FCB}\mathbf{U}\mathbf{V}\right\|^2_2+\lambda\sum_{n=1}^{K}\text{TGV}^2\{U_n\}$$with $$$\mathbf{s}$$$ the measured data, $$$\mathcal{F}$$$ the encoding operator, $$$\mathcal{C}$$$ the coil sensitivity operator, $$$\mathcal{B}$$$ the frequency shift operator and $$$\lambda$$$ the TGV regularization parameter. The reconstruction was preceded by skull-lipid suppression by orthogonality^8,10. The reconstructed MRSI dataset was quantified using LCModel¹².
Experimental tests
ECCENTRIC FID-MRSI data were acquired on a high resolution structural-metabolic phantom, two healthy volunteers and a brain tumor patient. Acceleration performance was assessed by retrospective undersampling and compared to fully sampled data by peak-SNR and SSIM of metabolic maps, and FWHM, CRLB, and SNR obtained from LCModel.

Results

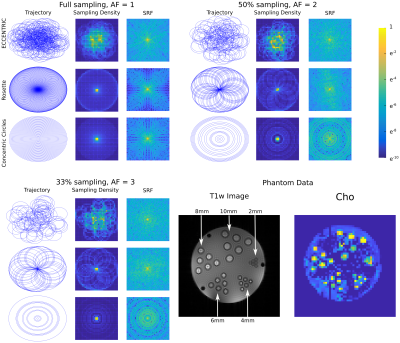
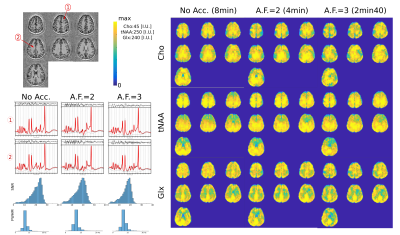
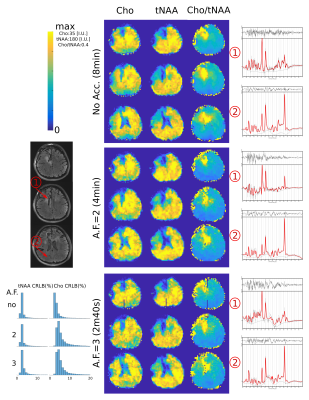
In Fig.2, we show the incoherent aliasing in SRF of undersampled ECCENTRIC and the SRF pattern is conserved for different AF. In comparison, rosette and concentric circles tend to create more coherent pattern when trajectories are undersampled, and their SRF changes with AF. This indicates that ECCENTRIC is more suitable for acceleration by compressed-sensing than these trajectories. The high-resolution phantom illustrates the capability to resolve structural features up to the acquired spatial resolution of 3.4mm. Reconstructed metabolite maps from a healthy volunteer are shown in Fig.3. The grey-white matter contrast particularly present in the Glx map indicates the sensitivity of the method for the lower signal of J-coupled metabolites. Spectral quality doesn't decrease strongly with acceleration. In Fig.4, brain tumor patient data are shown for Cho, tNAA and Cho/tNAA ratio maps. The tumor is clearly visible for all AF, although for AF=3 some areas of the healthy brain present more noise. Spectra show similar metabolic profiles for all AF, albeit a slight increase of noise. The apparent higher noise in patient data is due to a titanium plate and screws after brain surgery, which downgrades B₀ and B₁ homogeneity.

Discussion

We presented a new trajectory: ECCENTRIC that enables the acquisition of high-resolution MRSI without temporal interleaving and with random sparse sampling of the Fourier domain for unrestricted axial brain coverage, which has high potential for clinical applications. Work in progress explores higher spatial resolution and larger brain slab coverage with greater acceleration factors.

Acknowledgements

No acknowledgement found.