0784

iSLR: An Improved Shinnar-Le-Roux Frequency Selective Pulse Design Algorithm with Reduced Energy and More Accurate Phase Profiles

Frank Ong¹, Michael Lustig², Shreyas Vasanawala¹, and John Pauly¹
¹Stanford University, Stanford, CA, United States, ²University of California, Berkeley, Berkeley, CA, United States

Synopsis

The Shinnar-Le-Roux (SLR) algorithm is widely used for designing frequency selective pulses with large flip angles. We improve its design process to generate pulses with lower energy (by as much as 26%) and more accurate phase profiles.

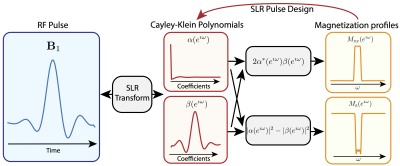
Concretely, the SLR algorithm consists of designing two polynomials that represent Cayley-Klein (CK) parameters. Because the CK polynomial pair is bi-linearly coupled, the original algorithm sequentially solves for each polynomial. This results in sub-optimal pulses.

Instead, we leverage a convex relaxation technique to jointly recover the CK polynomials. Our experiments show that the resulting pulses almost always attain the global solution in practice.

Introduction

The Shinnar-Le-Roux (SLR) algorithm^1-9 is widely used to design frequency selective pulses with large flip angles. Its pulses are routinely deployed on scanners for many functions, including slice excitation, spectral saturation, and spin-echo refocusing. In this work, we improve the SLR design process to generate pulses with lower energy (by as much as 26%) and more accurate phase profiles.

Concretely, the SLR algorithm consists of two steps:

an invertible transform between a frequency selective pulse and two polynomials that represent Cayley-Klein (CK) parameters
the design of the CK polynomial pair to match the desired magnetization profiles.

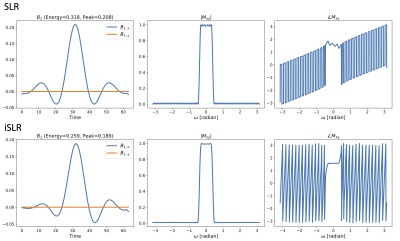
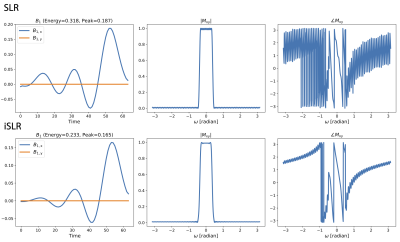
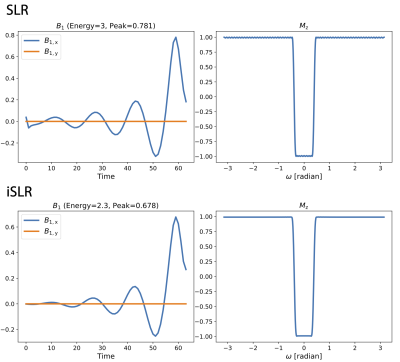
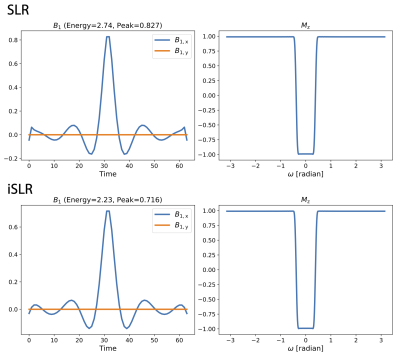
Because the CK polynomial pair is bi-linearly coupled, the original algorithm sequentially solves for each polynomial instead of jointly. This results in sub-optimal pulses.
Instead, we propose an improved SLR (iSLR) design process that can jointly solve for the CK polynomial pair. The new design can specify constraints directly on magnetization profiles, and optimize both CK polynomials to minimize pulse energy. In particular, we leverage a convex relaxation technique, commonly used for low rank matrix recovery, to address the bi-linearity. Our numerical experiments show that iSLR almost always attain the global solution in practice. For slice excitation, it results in more accurate linear phase profiles. And in general the improved pulses have lower energy than the original SLR pulses.

Related Works

Besides the original SLR algorithm, several works have been proposed with various tradeoffs. Barral et al.¹⁰ proposed a heuristic for the SLR algorithm to correct for phase profile errors. However, it does not jointly optimize the CK polynomials to minimize pulse energy. Another line of work^11-17 uses the inverse scattering transform, but the generated pulses have infinite length. Optimal control methods¹⁸ have also been extensively investigated for pulse design. However, the optimization problem is non-convex, which has no guarantees.

Problem Setup

The SLR algorithm considers the design of two polynomials that represent CK parameters to match some desired magnetization profiles.

Concretely, let $$$\omega$$$ represent a resonant frequency, $$$z=e^{\imath \omega}$$$ be the phasor and $$$n$$$ be the length of the discretized pulse, we denote the desired magnetization profiles as $$$M_{\mathrm{xy}}(z)$$$ and $$$M_{\mathrm{z}}(z)$$$, and the CK polynomials as

$$\alpha(z)=\sum_{i=0}^{n-1}a_{i}z^{-i},$$
$$\beta(z)=\sum_{i=0}^{n-1}b_{i}z^{-i},$$
where $$$a_i$$$ and $$$b_i$$$ represent the polynomial coefficients.

Assuming the initial magnetization starts from equilibrium, the CK polynomials and magnetization profiles are related as,
$$M_{\mathrm{xy}}(z)=2\beta(z)\alpha^*(z),$$
$$M_{\mathrm{z}}(z)=\alpha(z)\alpha^*(z)-\beta(z)\beta^*(z).$$
In addition, the CK polynomials must satisfy the following energy constraint:
$$\alpha(z)\alpha^*(z)+\beta(z)\beta^*(z)=1.$$

Note that the CK polynomials are bi-linearly coupled in all constraints. To bypass this, the original SLR sequentially solves for each polynomial instead of jointly. This results in sub-optimal pulses.

The Proposed Design Process

Instead, the proposed design process jointly designs the CK polynomials with a convex program. To derive the optimization problem, we first show that all constraints on the CK polynomials can be represented as linear equations on a rank-one matrix. Then we relax matrix rank constraints to positive semi-definite matrix constraints to obtain a convex program.

Concretely let us define the following vectors:
$$\psi(z)=\begin{pmatrix}1&z&\ldots&z^{n-1}\end{pmatrix}^T,$$
$$\mathbf{a}=\begin{pmatrix}a_{0}&a_{1}&\ldots&a_{n-1}\end{pmatrix}^T,$$
$$\mathbf{b}=\begin{pmatrix}b_{0}&b_{1}&\ldots&b_{n-1}\end{pmatrix}^T.$$
Then the CK polynomials can be expressed as,
$$\alpha(z) = {\psi}^*(z) \mathbf{a},$$
$$\beta(z) = {\psi}^*(z) \mathbf{b}.$$
Let us further define $$$\mathbf{P}$$$ as the outer product of the CK polynomial coefficients:
$$\mathbf{P}=\begin{pmatrix}\mathbf{P}_{aa}&\mathbf{P}_{ab}\\\mathbf{P}_{ba}&\mathbf{P}_{bb}\\\end{pmatrix}=\begin{pmatrix}\mathbf{a}\\\mathbf{b}\end{pmatrix}\begin{array}{@{}c@{}}\begin{pmatrix}\mathbf{a}^*&\mathbf{b}^*\end{pmatrix}\\\mathstrut\end{array}$$
Then, we can express the energy constraint and magnetization profiles in terms of $$$\mathbf{P}$$$ as follows:
$$1={\psi}^*(z)(\mathbf{P}_{aa}+\mathbf{P}_{bb}){\psi}(z)$$
$$M_{\mathrm{xy}}(z)=2{\psi}^*(z)\mathbf{P}_{ba}{\psi}(z)$$
$$M_{\mathrm{z}}(z)={\psi}^*(z)(\mathbf{P}_{aa}-\mathbf{P}_{bb}){\psi}(z)$$
Note that the above equations are all linear equations on $$$\mathbf{P}$$$.

Optimizing over rank-one matrices is in general non-convex. Therefore, a common strategy is to relax the rank constraint into a positive semi-definite matrix constraint. In particular, we can relax the constraint as follows
$$\mathbf{P}\succeq\begin{pmatrix}\mathbf{a}\\\mathbf{b}\end{pmatrix}\begin{array}{@{}c@{}}\begin{pmatrix}\mathbf{a}^*&\mathbf{b}^*\end{pmatrix}\\\mathstrut\end{array}.$$

Similar to the original SLR algorithm, we maximize $$$a_{0}$$$ to minimize pulse energy and $$$b_{0}$$$ to generate minimum phase pulses. Putting everything together, we obtain the following optimization problem:
$$\begin{aligned}&\text{max}&&\Re(a_{0})+\lambda_{\text{mp}}\Re(b_{0})\\&\text{s.t.}&&\mathbf{P}\succeq\begin{pmatrix}\mathbf{a}\\\mathbf{b}\end{pmatrix}\begin{array}{@{}c@{}}\begin{pmatrix}\mathbf{a}^*&\mathbf{b}^*\end{pmatrix}\\\mathstrut\end{array},\\&&&{\psi}^*(e^{\imath\omega})(\mathbf{P}_{aa}+\mathbf{P}_{bb}){\psi}(e^{\imath\omega})=1,\\&&&|2{\psi}^*(e^{\imath\omega})\mathbf{P}_{ba}{\psi}(e^{\imath\omega})-M_{\mathrm{xy}}(e^{\imath\omega})|\leq\delta_{\mathrm{xy}}(e^{\imath\omega}),\\&&&|{\psi}^*(e^{\imath\omega})(\mathbf{P}_{aa}-\mathbf{P}_{bb}){\psi}(e^{\imath\omega})-M_{\mathrm{z}}(e^{\imath\omega})|\leq\delta_{\mathrm{z}}(e^{\imath\omega}),\\&&&|{\psi}^*(e^{\imath\omega})\mathbf{b}-\beta(e^{\imath\omega})|\leq\delta_{\beta}(e^{\imath\omega}).\end{aligned}$$
where $$$\delta$$$ controls the maximum deviation from the desired profiles, and $$$\lambda_{\text{mp}}$$$ trades off between pulse energy and minimum phase.
In this work, we use the primal dual hybrid gradient method¹⁹ to solve the optimization problem.

Results

We used the improved algorithm to design pulses for excitation, inversion, saturation, and spin-echo refocusing pulses. Figures 2-5 show specific use cases with time-bandwidth of 8 and maximum deviation of 1%. For linear phase pulses, $$$\lambda_{\text{mp}}$$$ is set to zero. And for minimum phase pulses, $$$\lambda_{\text{mp}}$$$ is set to one.
For slice excitation, the proposed algorithm results in more accurate linear phase profiles. And in general the improved pulses have lower energy than the original SLR pulses. In all cases except for the minimum phase slice selection pulse, the relaxation is tight, that is $$$\mathbf{P}=\begin{pmatrix}\mathbf{a}\\\mathbf{b}\end{pmatrix}\begin{array}{@{}c@{}}\begin{pmatrix}\mathbf{a}^*&\mathbf{b}^*\end{pmatrix}\\\mathstrut\end{array}$$$. The improved pulses also have fewer discontinuities, commonly known as Connolly wings, when compared to the original ones.
In the spirit of reproducible research, we provide a software package to reproduce the results. The software package can be downloaded from: https://github.com/MRSRL/islr

Conclusion

We improve the SLR design process to generate pulses with lower energy (by as much as 26%) and more accurate phase profiles. The proposed SLR algorithm can potentially accelerate SAR-limited sequences and enable the design of excitation profiles with arbitrary phase.

Acknowledgements

We thank NIH R01 EB009690 and NIH U01EB029427 for support.

References

[1] M. Shinnar and J. S. Leigh, “The application of spinors to pulse synthesis and analysis,” Magnetic Resonance inMedicine, vol. 12, no. 1, pp. 93–98, Oct. 1989. [Online]. Available: http://doi.wiley.com/10.1002/mrm.1910120112

[2] M. Shinnar, S. Eleff, H. Subramanian, and J. S. Leigh, “The synthesis of pulse sequences yielding arbitrary magnetization vectors,” Magnetic Resonance in Medicine, vol. 12, no. 1, pp. 74–80, Oct. 1989. [Online]. Available: http://doi.wiley.com/10.1002/mrm.1910120109

[3] M. Shinnar, L. Bolinger, and J. S. Leigh, “The synthesis of soft pulses with a specified frequency response,” Magnetic Resonance in Medicine, vol. 12, no. 1, pp. 88–92, Oct. 1989. [Online]. Available: http://doi.wiley.com/10.1002/mrm.1910120111

[4] ——, “Use of finite impulse response filters in pulse design,” in Proceedings of the 7th Annual Meeting and Exhibition of the Society for Magnetic Resonance in Medicine, San Francisco, CA, USA, 1988, p. 695, eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/mrmp.22419880204. [Online]. Available: https://onlinelibrary.wiley.com/ doi/abs/10.1002/mrmp.22419880204

[5] ——, “The use of finite impulse response filters in pulse design,” Magnetic Resonance in Medicine, vol. 12, no. 1, pp. 81–87, Oct. 1989. [Online]. Available: http://doi.wiley.com/10.1002/mrm.1910120110

[6] P. Le Roux, “Exact Synthesis of Radiofrequency Waveforms,” in Proceedings of the 7th Annual Meeting and Exhibition of the Society for Magnetic Resonance in Medicine, San Francisco, CA, USA, Aug. 1988, p. 1049, eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/mrmp.22419880211. [Online]. Available: https://onlinelibrary.wiley.com/ doi/abs/10.1002/mrmp.22419880211

[7] ——, “Method of radio-frequency excitation in an NMR experiment,” US Patent US4940940A, Jul., 1990, library Catalog: Google Patents. [Online]. Available: https://patents.google.com/patent/US4940940/en

[8] ——, “Simplified RF Synthesis,” in Proceedings of the 8th Annual Meeting and Exhibition of the Society for Magnetic Resonance in Medicine, vol. 1989, Amsterdam, The Netherlands, Aug. 1989, p. 1168, eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/mrmp.22419890305. [Online]. Available: https://onlinelibrary.wiley.com/doi/abs/10.1002/mrmp.22419890305

[9] J. Pauly, P. L. Roux, D. Nishimura, and A. Macovski, “Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm (NMR imaging),” IEEE Transactions on Medical Imaging, vol. 10, no. 1, pp. 53–65, Mar. 1991.

[10] J. K. Barral, J. M. Pauly, and D. G. Nishimura, “SLR RF Pulse Design for Arbitrarily-Shaped Excitation Profiles,” in Proceedings of the ISMRM 16th Annual Meeting, Toronto, ON, Canada, May 2008, p. 1323.

[11] C. L. Epstein, “Introduction to magnetic resonance imaging for mathematicians,” Annales de l’institut Fourier, vol. 54, no. 5, pp. 1697–1716, 2004. [Online]. Available: https://aif.centre-mersenne.org/item/AIF 2004_54_5_1697_0/

[12] C. L. Epstein and J. F. Magland, “Inverse Scattering Pulse Design,” in eMagRes. American Cancer Society, 2012, eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/9780470034590.emrstm1303. [Online]. Available: http: //onlinelibrary.wiley.com/doi/abs/10.1002/9780470034590.emrstm1303

[13] C. L. Epstein, “Minimum energy pulse synthesis via the inverse scattering transform,” Journal of Magnetic Resonance, vol. 167, no. 2, pp. 185–210, Apr. 2004. [Online]. Available: https://linkinghub.elsevier.com/retrieve/pii/S1090780703004439

[14] ——, “Minimum energy pulse synthesis via the inverse scattering transform,” Journal of Magnetic Resonance, vol. 167,no. 2, pp. 185–210, Apr. 2004. [Online]. Available: http://linkinghub.elsevier.com/retrieve/pii/S1090780703004439

[15] J. F. Magland, “Discrete Inverse Scattering Theory for NMR Pulse Design,” arXiv:0903.4363 [math-ph], Mar. 2009,arXiv: 0903.4363. [Online]. Available: http://arxiv.org/abs/0903.4363

[16] J. Magland and C. L. Epstein, “Exact half pulse synthesis via the inverse scattering transform,” Journal of MagneticResonance, vol. 171, no. 2, pp. 305–313, Dec. 2004. [Online]. Available: https://linkinghub.elsevier.com/retrieve/pii/S1090780704003040

[17] ——, “Practical pulse synthesis via the discrete inverse scattering transform,” Journal of Magnetic Resonance, vol. 172, no. 1, pp. 63–78, Jan. 2005. [Online]. Available: http://linkinghub.elsevier.com/retrieve/pii/S1090780704002800

[18] S. Conolly, D. Nishimura, and A. Macovski, “Optimal Control Solutions to the Magnetic Resonance Selective Excitation Problem,” IEEE Transactions on Medical Imaging, vol. 5, no. 2, pp. 106–115, Jun. 1986, conference Name: IEEE Transactions on Medical Imaging.

[19] A. Chambolle and T. Pock, “A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging,” Journal of Mathematical Imaging and Vision, vol. 40, no. 1, pp. 120–145, May 2011. [Online]. Available: http://link.springer.com/10.1007/s10851-010-0251-1

Figures

An overview of the SLR algorithm, which has two steps: (1) an invertible transform between a frequency selective pulse and two polynomials that represent Cayley-Klein (CK) parameters and (2) the design of the CK polynomial pair to match a desired magnetization profile. Because the CK polynomial pair is bi-linearly coupled, the original algorithm sequentially solves for each polynomial instead of jointly. Instead, we leverage a convex relaxation technique, commonly used for low rank matrix recovery, to address the bi-linearity.

Linear phase slice selection pulses and their transverse magnetization profiles after refocusing. The improved SLR (iSLR) pulse has a much flatter phase response than the original one. Pulse energy is reduced by 18.6% and peak is reduced by 9.1%. Note that the improved pulse is asymmetric, which shows that the proposed design compensates for the phase of α to generate a linear phase profile.

Minimum phase slice selection pulses and their transverse magnetization profiles. Pulse energy is reduced by 26.7% and peak is reduced by 11.8%.

Minimum phase inversion pulses and their longitudinal magnetization profiles. Pulse energy is reduced by 23.3% and peak is reduced by 13.2%.

Zero phase spin-echo refocusing pulses and their longitudinal magnetization profiles. Pulse energy is reduced by 18.6% and peak is reduced by 13.4%.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0784