Introduction

Ultra-high field (UHF, ≥7T) MRI promises unprecedented SNR and contrasts, and parallel transmission (pTx) system is now a standard add-on for UHF MRI. However, for 2D multislice imaging there is not a simple and robust algorithm for RF shimming and STA multi-spoke pulse design. A major issue is the conventional magnitude-least-squares (MLS) algorithm [1] would converge with a flip angle (FA) null in the ROI (e.g. Ref2 Fig1, Ref3 Fig4a). Prior efforts with random initialization [4], region growing [5], quadratic programming [6], and evolution strategy [7] were either not effective or over-complicated. Here a finite-difference-regularized MLS (FD-MLS) is proposed that avoids erroneous null solutions for both RF shimming and STA multi-spoke pulses, and improves the monotonicity of the FA error and RF power trade-off relationship ("L-curve") for the latter, hence it streamlines patient-tailored 2D multislice imaging with UHF MRI.

Theory

To improve the robustness of the solutions for both RF shimming [8] and STA multi-spoke pulses [9], a finite-difference regularizer is added to MLS:
$$\min_{x} \{|||Ax|-1||^2 + \beta_1||x||^2 + \beta_2|| \nabla(Ax)||^2\}$$
$$$A$$$ is the pTx system matrix; $$$x$$$ is the pTx pulse weight vector; $$$\nabla$$$ is a FD operator, which performs complex subtractions between adjacent image voxels in 2D; $$$\beta_1$$$ scales RF power to calculate the L-curve; $$$\beta_2$$$ is described below. For simplicity, all designs target 1 degree FA.

The FD-MLS is solved similarly as MLS with iterative RF weights $$$x$$$ and target phase $$$\phi$$$ updates:
$$\min_{x} \{||Ax-\textrm{exp} (i\phi)||^2 + \beta_1||x||^2 + \beta_2|| \nabla (Ax) ||^2\}$$
and
$$x_{n}=(A^*A+\beta_1I+\beta_{2,n}( \nabla A)^*( \nabla A))^{-1} (A^*\textrm{exp}(i\phi_n))$$
The target phase $$$\phi_n$$$ is typically initialized as quadrature B₁⁺ phase, and the achievable FA phase for subsequent iteration $$$n$$$:
$$\phi_{n} \leftarrow \angle(Ax_{n-1}) \hspace{0.5cm} \textrm{if } n > 1 \textrm{ or if } \beta_{2,n-1} > 0$$
$$$\beta_{2,n}$$$ characterizes the severity of the null by counting the voxels in achievable FA map below a given threshold $$$\alpha_2$$$ and scale it with $$$\alpha_1$$$.
$$\beta_{2,n} = \Big\{ \begin{matrix}0 & \textrm{if } n = 1 \textrm{ or if } \beta_{2,n-1} > 0\\ \alpha_1 \sum_{i \in \{ |Ax|_i < \alpha_2 \}} 1 & \textrm{if } n > 1 \textrm{ and } \beta_{2,n-1} = 0 \end{matrix}$$
After every time $$$\beta_{2,n}$$$ is non-zero, the iteration counter $$$n$$$ is reset to 1. Typically $$$\alpha_1=1.5$$$ and $$$\alpha_2=0.08-0.3$$$ are used with $$$\alpha_2$$$ linearly decreasing to 0 after an FD iteration limit (typically 30), and consequently the FD regularization eventually deactivates. Choices of larger $$$\alpha_1>1.5$$$ and especially $$$\alpha_2>0.08$$$ further improve the algorithm against other local minimum solutions. In practice, $$$\alpha_2$$$ can be minimized with the same B₁⁺ protocol and coil used from a population of subjects to minimize computation time. The FD-MLS can be further combined with random initialization and evolution strategy.

Method

The FD-MLS was evaluated with human brain and knee data at 7T. Whole brain B₁⁺ maps were collected using 2D MS TFE based DREAM[10] (STEAM FA=30^o, TR=4.5s) and Tx-cycled 3D GRE (FA=0.5^o, TR=5ms) with the Nova 8Tx32Rx head coil in less than 5 mins. Slice-by-slice dynamic RF shimming was performed for GRE-ssEPI-based fMRI (voxel size=2x2x2mm³, FA=68^o, TE/TR=28ms/2s). The protocol for knee data was reported in Ref11.

Result & Discussion

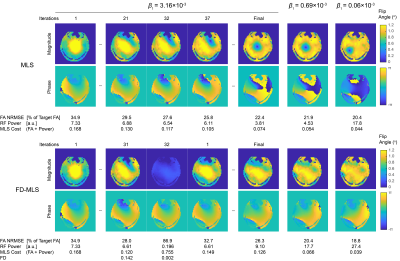
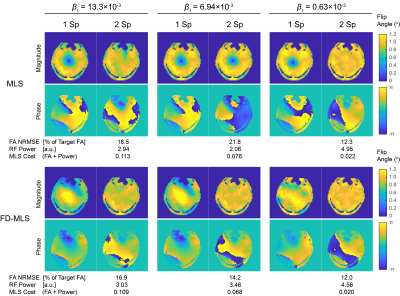
Fig 1 shows how FD-MLS functions against null solutions for RF shimming. It iteratively detects null based on thresholding, finds homogeneous FA solutions in both magnitude and phase with FD (iteration 32), and passes the FD-optimized phase as the next target phase. Note, it also shows that the null sometimes is the global minimum with smaller MLS cost ($$$\beta_1=0.69×10^{-3}$$$) and even smaller FA NRMSE ($$$\beta_1=3.16×10^{-3}$$$), underscoring the importance for the extra FD regularizer.

Fig 2 shows the advantage of FD-MLS over MLS for 2-spoke STA pulse. While the addition of spokes helped with the null, it was still formed with MLS especially when RF power was moderately regularized ($$$\beta_1=6.94×10^{-3}$$$), and the null from the intermediary 1-spoke solution negatively impacted the 2-spoke result ($$$\beta_1=13.3×10^{-3}$$$). All were resolved with FD-MLS.

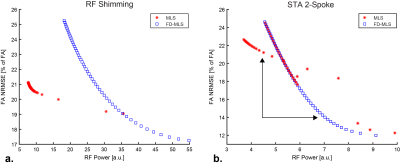
Fig 3 shows the detailed L-curves from Figs 1&2. These figures show that FD-MLS is effective in avoiding null solutions and in improving the monotonicity of the L-curves. They also show substantially decreased RF power for STA multi-spoke pulses than RF shimming, as expected. Thus FD-MLS may be especially valuable to simultaneous multislice excitation with low power multi-spoke pulses.

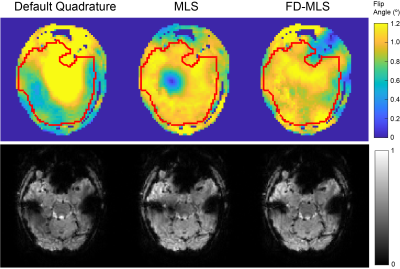
Fig 4 shows GRE-EPI images comparing different pulsing strategies. With fixed system gain, FD-MLS enabled the best image with enhanced signal intensity and SNR. The experimental image intensities (bottom row) are consistent with predicted and designed FA distribution (top row).

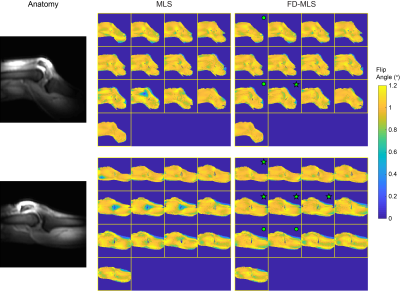
Fig 5 shows the success and robustness of the FD-MLS by evaluating two 8-channel transmit knee array datasets with different postures, with dynamic multislice RF shimming using identical $$$\alpha_1$$$ and $$$\alpha_2$$$ parameters as the above brain imaging.

Conclusion

The FD-MLS is demonstrated effective in avoiding erroneous solution with an excitation null for RF shimming and STA multi-spoke pulses, and in improving the monotonicity of the trade-off relationship between FA error and RF power for the latter. The tuning parameters ($$$\alpha_1$$$, $$$\alpha_2$$$) are demonstrated robust across different coil geometries, body parts and B₁⁺ mapping protocols. Overall, the FD-MLS provides major practical value in streamlining patient-tailored pTx operations.

Acknowledgements

Special thanks to Jin Jin from University of Queensland and Siemens Healthcare for sharing the 8Tx knee data.