Introduction

Magnetic resonance current density imaging (MRCDI)¹ and magnetic resonance electrical impedance tomography (MREIT)² are two emerging techniques that can produce low-frequency current density and conductivity distributions, respectively using MR measurements of the z-component of the magnetic flux density (B_z) data induced due to external current injection. While the current density can be straightforwardly estimated using a single set of B_z data, the stable reconstruction of the conductivity distribution using MREIT requires data from two independent current administrations². Administration of two independent currents are not normally possible in DBS settings.
MRCDI has already been used to demonstrate current pathways during deep brain stimulation (DBS)^3,4 therapy. However, it is not possible to find the corresponding electric field distributions due to the lack of a stable conductivity reconstruction method. Recently, Song et al.⁵ developed an iterative single-current algorithm that can stably reconstruct the ‘apparent’ conductivity distribution from data obtained using a single current administration by converting the first-order hyperbolic partial differential equation (PDE) used in the Harmonic B_z MREIT reconstruction algorithm² into a second-order elliptical-PDE. The aim of this study is to demonstrate the capability of the new single-current harmonic B_z algorithm to characterize electromagnetic field distributions produced by DBS electrodes.

Methods

Phantom design: A head-shaped phantom formed of agarose-gel was used in this study⁴. At 10 Hz, the gel conductivity was measured to be 0.75 S/m. A directional DBS electrode (Abbott Infinity 6172, Abbott, Abbott Park, IL, USA) was inserted near the phantom center (Fig.1b). A 50 x 50 mm² carbon return electrode (HUREV Co Ltd, South Korea) was also attached at the occipital (Oz) location (Fig.1b). We placed a piece of chicken muscle between DBS lead and Oz electrode (Fig.1b) to form a conductivity contrast. An MR safe electrical stimulator (DC-STIMULATOR MR, neuroConn, Ilmenau, Germany) was used to deliver a 1.0 mA current between the DBS electrode contact combinations and the return Oz electrode. In the DBS-1-Oz setting, the omni-directional electrode contact-1 (Fig.1a) of the electrode and Oz were used, and the DBS-2B-Oz setting denoted the use of the sectional electrode contact-2B (Fig.1a) facing towards the Oz direction. This allowed evaluation of the differences between electric fields produced using conventional omnidirectional DBS electrodes and newer directional DBS electrode designs.
Magnetic flux density measurement: All MR data were measured using a 32-channel RF coil in a 3.0T Phillips scanner (Phillips, Ingenia, Netherlands) located at the Barrow Neurological Institute (Phoenix, Arizona, USA). Current induced B_z data was measured at three axial slice positions using the Phillips mFFE pulse sequence with an imaging matrix size of 128 x 128 and field-of-view 224x224 mm². Other imaging parameters were TR/TE = 50/7 ms, number of echoes = 10, echo spacing = 3 ms, number of averages = 24. The total scan time was 6 min. A set of T1-weighted images with matrix size, 224x224x224 resulting in 1 mm³ isotropic resolution, were also collected during the imaging session to build a numerical model of the phantom and wiring⁶. Prior to estimating the electromagnetic field parameters, the echo combined⁷ optimized B_z images were corrected to account for wire-created stray magnetic-fields (Fig 1e-f).
Reconstruction of electromagnetic parameters: We first used the stray-field-corrected B_z data to reconstruct the current density distribution, $$$ \mathbf{\mbox{J}}^{P,R}$$$, within the local region $$$R$$$, (Fig. 1d) using the regional projected current density algorithm⁸. From the $$$ \mathbf{\mbox{J}}^{P,R}$$$, and the known conductivity, ($$$\sigma_{b}$$$), at the tissue boundary $$$\partial R$$$, the first-update of the internal conductivity distribution, $$$\sigma^1$$$ was reconstructed as⁵
$$ \begin{cases}\triangledown_{xy}^2 ln\sigma^{1}=\frac{1}{\mu_{0}}\triangledown_{xy} .\Bigg( -\frac{J_y^{P,R}}{(J_x^{P,R})^{2}+{(J_y^{P,R})^{2}}}\triangledown_{xy}^2B_{z},~\frac{J_x^{P,R}}{(J_x^{P,R})^{2}+{(J_y^{P,R})^{2}}}\triangledown_{xy}^2B_{z} \Bigg)~~~~~~in~~~ R~~~~~~~~~~~~~~~~~~~~~~~(1)\\\\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ln \sigma^{1}=ln \sigma_{b}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~on ~~\partial R \end{cases}$$
where $$$\mu_{0}$$$ denotes the permeability in free space. We set $$$\sigma_{b}$$$ =0.75 S/m.
The corresponding electric field distribution was then found using Ohm’s law
$$\mathbf{\mbox{E}}=\frac{\mathbf{\mbox{J}}^{P,R}}{\sigma}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(2)$$

Results

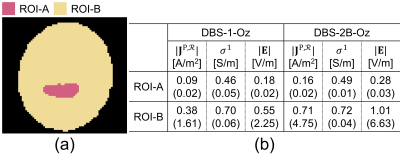
Figs. 2a (i) and (iv) show the reconstructed $$$ \mid \mathbf{\mbox{J}}^{P,R} \mid $$$distribution due to the 1.0 mA current injected using the DBS-1-Oz and DBS-2B-Oz electrode configurations, respectively. Reconstructed $$$\sigma^{1}$$$ distributions measured using the DBS-1-Oz and DBS-2B-Oz configurations are displayed in Figs. 2b (ii) and (v), respectively. The corresponding electric field magnitudes found using Eq. 2 are shown in Fig 2c (iii) and (vi). All reconstructed electromagnetic field parameters within the chicken muscle and agar background are summarized in the table in Fig 3.

Discussion

As noted in⁵, the first update to the iterative reconstruction method $$$\sigma^{1}$$$ is sufficient to produce a result comparable with the two-current-injection non-iterative harmonic B_z algorithm⁹. Therefore, in this study, we only use the first-updated to the conductivity distribution to determine electromagnetic field parameters. In the case of the reconstructed $$$ \mid \mathbf{\mbox{J}}^{P,R} \mid$$$ and $$$\bf \mid E \mid$$$ fields (Fig. 3) we also found high standard deviations in the background agar region, which stems from the fact that most of the field distribution is concentrated nearby the DBS electrode region (Fig. 2(a), (c)). However, as expected this high field nearby the DBS electrode does not affect the reconstructed conductivity in the agar region (Fig. 3b).

Conclusion

We have demonstrated that it is possible to characterize electromagnetic properties and fields deep within the brain using DBS electrode illumination using a biological tissue phantom.

Acknowledgements

This work was supported by award RF1MH114290 to RJS.