0732

Spatiotemporal encoding for DWI of brain and prostate using subspace-constrained sampling and locally-low-rank regularized reconstruction

Martins Otikovs¹, Ankit Basak¹, and Lucio Frydman¹
¹Weizmann Institute of Science, Rehovot, Israel

Synopsis

The benefits of performing locally low-rank (LLR) reconstruction on subsampled diffusion weighted (DW) data employing spatiotemporal encoding (SPEN) methods, is investigated. SPEN allows for self-referenced correction of motion-induced phase errors in case of interleaved DW acquisitions, and allows to overcome distortions otherwise observed along EPI’s phase-encoded dimension. In combination with LLR regularization and with joint subsampling of b-weighted and interleaved images, additional improvements are demonstrated. The method is tested on phantoms, and improvements in in-vivo brain and prostate scans on volunteers are demonstrated.

Introduction

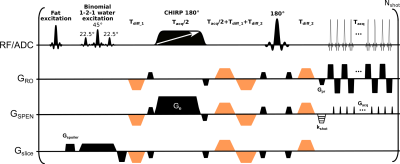
Diffusion weighted imaging (DWI) usually relies on variations of echo planar imaging (EPI). A common approach to increase EPI’s resolution and SNR is by using segmentation, for instance phase-encode (PE) interleaving. Incorporation of locally low-rank (LLR) regularization^1,2 has been shown beneficial for segmented EPI acquisitions when sampling various diffusion directions, thanks to the redundancy derived from the multiple acquisitions.³ In parallel, a suitable choice of basis functions that accounts for the expected signal evolution, has been shown to further accelerate the image acquisitions in subspace-constrained DW contexts.⁴

Here we combine these concepts and explore their use with an alternative ultrafast imaging technique, spatiotemporal encoding (SPEN).⁵ SPEN (Figure 1) replaces EPI’s PE with a quadratic phase encoding and subsequent gradient-driven decoding, to provide higher immunity to magnetic field inhomogeneities.^6,7 Images reconstructed from multiple interleaved SPEN acquisitions, do not suffer from aliasing artifacts associated with analogous reconstructions from subsampled EPI data. This allows to estimate motion induced phase variations on a per-shot basis and account for them during reconstruction in a self-referenced manner.⁸ This study explores the consequences of these advantages, in combination with LLR-regularization and with the joint sampling of the diffusion and imaging sub-spaces.

Methods

SPEN signals y were forward-modelled as $$$y=P\cdot A\cdot S\cdot x$$$. Here x is the image being sought, S is the coil sensitivity map, A corresponds to a multiplication by a super-resolution matrix akin to EPI’s Fourier transform accounting for SPEN’s quadratic phase encoding,⁹ and P is a sampling operator accounting for the multi-shot interleaving. LLR regularization^1,2 adds to these constraints, by imposing spatial correlations among the b-weighted images. To do so an operator R_r extracts a block from each image centered around voxel r, reshapes each block into a matrix column, applies a nuclear norm to each matrix weighted by a regularization parameter λ, and subsequently sums all results for delivering a final image: $$\min_{x}\frac{1}{2}\parallel y-P\cdot A\cdot S\cdot x\parallel _2^2 + \lambda\sum_r\parallel R_{r}(x) \parallel _{*} (1)$$
To deal with the multi-b-weighting this model was modified by using a subspace where the minimum number of K eigenvectors {Φ_k=1,K} are selected. This is done such that ||X-ΦΦ^HX|| < ε, where Φ is an orthonormal basis describing the b-weighting and ε a chosen tolerance. Denoting {α= Φ^Hx} as the target to be solved, reconstruction was formulated as the minimization problem:
$$\min_{\alpha}\frac{1}{2}\parallel y-P\cdot A\cdot S\cdot \Phi\cdot\alpha\parallel _2^2 + \lambda\sum_r\parallel R_{r}(x) \parallel _{*} (2)$$

MRI data were acquired at 3T on a Siemens Prisma on phantoms and on suitably consenting volunteers.

Results & Discussion

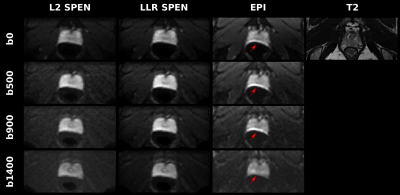
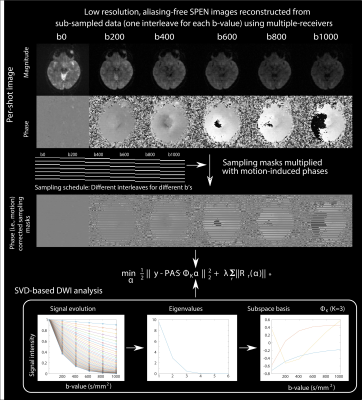
Before testing the joint subspace sampling model, Figure 2 compares the outcome of the Eq. (1) model for processing prostate DWI SPEN data, against results arising from an L2-based forward reconstruction⁸ and against EPI. Both SPEN processings can reduce field distortions evident next to the rectum, while LLR provides better SNR. The LLR methodology was then tested in conjunction with the model in Eq. (2); results from this joint sampling approach on a phantom are illustrated in Figure 3. Images resulting from 6 interleaved segments and from 6 different b-values in the 0-1000 s/mm² range, were retrospectively undersampled; only one segment was kept for each b-value. While in such case two images with different diffusion weightings suffice to calculate the ADC maps, this shows that the approach can be used to obtain the desired contrast/map with improved resolution, with only a fraction of the data.

This methodology had to be modified for processing in-vivo data, to deal with motion corrections. The approach taken is outlined in Figure 4, along with corresponding brain images. Motion-associated phase errors were accounted for by reconstructing an alias-free, medium-quality image from each shot’s SPEN data using SUSPENSE.¹⁰ The derived per-shot phase maps were applied to the sampling masks to account from inter-scan motion, and then combined with the SVD-based multi-b decomposition analysis (K=3).

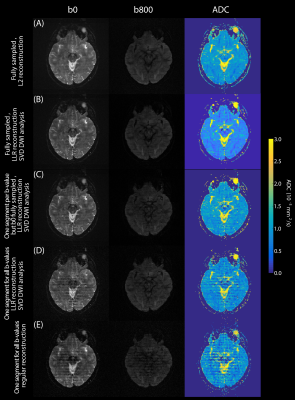
Figure 5 explores further the influence of this subspace-constrained reconstruction on the quality of the resulting DWI and ADC maps. For full sampling, LLR’s improvements are marginal (A, B); yet when jointly undersampling image and b-spaces, LLR can still provide quality data where other schemes do not. Notice as well the advantages of fully sampling the b=0 s/mm² image while substantially undersampling other b-values, for delivering artifact-free images (Fig. 5C).

Conclusion

This work demonstrates that good SNR and artifact-immunity performances can arise for jointly subspace-sampled SPEN DW data, processed by LLR reconstruction. LLR regularization alone also improves SNR for SPEN images vs L2 regularized processing in conventional DWI.

Acknowledgements

This work was funded by the Israel Science Foundation via grants 2508/17 and 965/18, by the Sheba MC - Weizmann Institute Joint Research Program, and by the generosity of the Perlman Family Foundation.

References

1. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn Reson Med 2015; 73:655–661.

2. Kim K, Ye JC, Worstell W, et al. Sparse-view spectral CT reconstruction using spectral patch-based low-rank penalty. IEEE Trans Med Imaging 2015; 34:748–760.

3. Hu Y, Wang X, Tian Q, et al.: Multi‐shot diffusion‐weighted MRI reconstruction with magnitude‐based spatial‐angular locally low‐rank regularization (SPA‐LLR). Magn Reson Med 2020; 83:1596–1607.

4. Wen Q, Feng L, Zhou K, Wu YC. Rapid golden-angle diffusion-weighted propeller MRI for simultaneous assessment of ADC and IVIM. NeuroImage 2020; 223:117327.

5. Shrot Y, Frydman L. Spatially encoded NMR and the acquisition of 2D magnetic resonance images within a single scan. J Magn Reson 2005; 172:179–190.

6. Tal A, Frydman L. Spatial encoding and the single-scan acquisition of high definition MR images in inhomogeneous fields. J Magn Reson 2006 182:179–194.

7. Ben Eliezer EN, Shrot Y, Frydman L. High-definition, single-scan 2D MRI in inhomogeneous fields using spatial encoding methods. J Magn Reson Imaging 2010, 28:77–86.

8. Cousin SF, Liberman G, Solomon E, et al. A regularized reconstruction pipeline for high‐definition diffusion MRI in challenging regions incorporating a per‐shot image correction. Magn Reson Med 2019; 82:1322–1330.

9. Ben Eliezer EN, Irani M, Frydman L. Super-Resolved Spatially Encoded Single-Scan 2D MRI. Magn Reson Med 2010 63:1594–1600.

10. Liberman G, Solomon E, Lustig M, Frydman L. Multiple‐coil k‐space interpolation enhances resolution in single‐shot spatiotemporal MRI. Magn Reson Med 2018; 79:796–805.

11. Schmidt R, Frydman L: New spatiotemporal approaches for fully refocused, multislice ultrafast 2D MRI. Magn Reson Med 2014; 71:711–722.

Figures

Figure 1. SPEN pulse sequence used in this study, including DW gradients (orange), N_shot interleaved scans, and incorporating a fat-saturation / binomial water excitation block. Timings indicated were set to fulfill full-refocused acquisition conditions¹¹. G_e, encoding gradient; G_slice, slice-selective direction; G_spen, SPEN-encoded direction gradients; G_ro, readout direction; G_acq, blipped acquisition gradients; T_acq, acquisition time; N_shot, number of interleaves, including different values of the k_shot gradient.

Figure 2. Healthy volunteer prostate DWI exam comparing trace-weighted SPEN images reconstructed using L2 regularization,⁸ using LLR regularization, and EPI. The latter shows the most clear distortions caused by air interfaces vs the anatomical T2w image (arrows), while LLR yields an improved SNR. DW images were acquired at 2.4x2.4x3 mm³ with b-values (repetitions) of 50 (1), 500 (1), 900 (5) and 1400 (12), except for EPI, where b=50 and 500 s/mm² were acquired using five repetitions.

Figure 3. Left: ACR phantom images for 6 b-values, each of them reconstructed from a set of six interleaved SPEN data acquisitions following the processing described in Ref. 8. Center: Idem but from a set of undersampled data, using only one of the interleaved scans per b-value and following Eq. (2). Right: ADC maps calculated from b=0 and 800 s/mm² DW images by both methods. For the subspace LLR reconstruction diffusion was modeled using K=2 eigenvectors after SVD of monoexponential functions modeling signal attenuation as function of b for ADCs in the 0.1-5x10-3 s/mm² range.

Figure 4. Outline of the motion-corrected subspace-constrained LLR reconstruction adopted here for processing in-vivo SPEN data. The schedule includes a limited number of interleaved shots per b-value (1 out of 6 in this example), corrected for potential motions by phase correction after using the SUSPENSE reconstruction in Ref. 10. Coupled to this was the SVD-based analysis of the DW behavior.

Figure 5. Comparing different strategies for processing a 6-b-value (0-1000 s/mm²) SPEN experiment. (A) Usual DWI reconstruction, illustrating two b-valued images and the resulting ADC map.⁸ (B) Same but with constrained DW subspace LLR reconstruction on the full set. (C) Idem as in B, but for data with a fully sampled b=0 image and only one shot for the other b’s. (D) Idem as C, but a single shot also used for the b=0 image reconstruction. (E) Same as D, but using reconstruction in Ref. 10. Data in B-E were obtained undersampling acquisition of 6 segments at 1.2x1.2x3 mm³ resolution.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0732