Introduction

Myelin water fraction (MWF) mapping is emerging as a powerful tool for studying demyelinating diseases such as multiple sclerosis.¹ The key to MWF mapping is separation of myelin water from other water components; this is often achieved via exponential model fitting, which exploits the short $$$\text{T}_2$$$ or $$$\text{T}_2^*$$$ characteristics of myelin water.^1-2 However, one fundamental issue with exponential model fitting is its highly ill-conditioned nature, making current methods very sensitive to noise and modelling errors, especially for $$$\text{T}_2^*$$$-based MWF mapping.^3-4 To address this problem, a new MWF estimation method has been proposed, which uses an extended signal model to compensate for practical signal variations and incorporates pre-learned parameter distributions and low-rank signal structure to improve parameter estimation. Both simulation and experimental results show that the proposed method outperforms the conventional schemes with significantly enhanced robustness.

Methods

(1) Signal Model
Conventional MWF models often have significant errors in representing practical $$$\text{T}_2^{*}$$$-weighted imaging data due to large signal distortions coming from practical imaging conditions (e.g., field inhomogeneity and drift). To address this problem, we propose a new model with a build-in capability to absorb signal variations that deviate from the conventional MWF models. More specifically, we represent the magnitude signal using the following compensated 3-exponential model:
$$\hspace{8em}s(t)=\left(\sum_{c}\text{A}_{c}e^{-t/\text{T}_{2,c}^*}\right)\sum_{\ell=-L/2}^{L/2}b_{\ell}e^{i2\pi\ell\Delta{f}t}+\epsilon(t)\quad\text{subject}\;\text{to}\quad{b_{-\ell}=b_{\ell}^*}\hspace{8em}[1]$$
which uses a finite impulse response (FIR) filter to compensate for non-exponential decays. In Eq. [1], $$$c$$$ represents tissue component, denoting myelin water (MW), axonal water (AW), or extra-cellular water (EM); $$$\Delta{f}$$$ is the spectral resolution, $$$b_{\ell}^*$$$ the conjugate of $$$b_{\ell}$$$, and $$$\epsilon$$$ the noise term.

We further impose statistical distributions on the model parameters to constrain the parameter variations, i.e., $$$\text{A}_{c}\sim\text{Pr}(\text{A}_c)$$$ and $$$\text{T}_{2,c}^*\sim\text{Pr}(\text{T}_{2,c}^*)$$$. Here, $$$\text{Pr}(\text{A}_c)$$$ and $$$\text{Pr}(\text{T}_{2,c}^*)$$$ are represented by a mixture of Gaussians (MoG) given its computational simplicity and ability to represent practical density functions.⁵

(2) MWF Estimation
Learning of the Parameter Distributions
In this work, $$$\text{Pr}(\text{A}_c)$$$ and $$$\text{Pr}(\text{T}_{2,c}^*)$$$ were learned from training data obtained in vivo. More specifically, we fit the training data with the conventional 3-exponential model and the estimated parameters from different voxels were treated as samples drawn from the desired distributions (i.e., $$$\text{Pr}(\text{A}_c)$$$ and $$$\text{Pr}(\text{T}_{2,c}^*)$$$). From these samples, we determined the corresponding MoG parameters under the maximum likelihood (ML) principle.

Bayesian-Based Parameter Estimation
The learned parameter distributions were incorporated into the solutions by fitting the proposed model to the measured data in the Bayesian sense:
$$\hspace{1.8em}\bar{\text{A}}_{c},\bar{\text{T}}_{2,c}^{*},\bar{b}_{\ell}=\text{arg}\min_{\text{A}_{c}\text{T}_{2,c}^*b_{\ell}}\frac{1}{\sigma^2}\left\lVert{s(t)-\left(\sum_{c}\text{A}_{c}e^{-t/\text{T}_{2,c}^*}\right)\sum_{\ell=-L/2}^{L/2}b_{\ell}e^{i2\pi\ell\Delta{f}t}}\right\rVert_2^2-\sum_{c}\log\left(\text{Pr}\left(\text{A}_c\right)+\text{Pr}\left(\text{T}_{2,c}^*\right)\right)\hspace{1.8em}[2]$$
where $$$\sigma^2$$$ is the noise variance. Eq. [2] was solved using the majorization-minimization algorithm.⁶

Instead of treating the solutions from Eq. [2] as the final values for the model parameters, we further constrained the long-$$$\text{T}_{2}^{*}$$$ components (i.e., the AW and EW pools) by forcing them to belong to a subspace in the probabilistic sense, i.e.,
$$\hspace{13.2em}s_{l}(t)=\sum_{r}a_{r}\phi_{r}(t)\quad\text{with}\quad\{a_{r}\}\sim\text{Pr}\left(\{a_{r}\}\right)\hspace{13.2em}[3]$$
This additional constraint was motivated by our observations that estimation variation of the long-$$$\text{T}_{2}^{*}$$$ components could significantly influence the estimation of the MW; therefore, we leveraged the inherent low-rank structure of the long-$$$\text{T}_{2}^{*}$$$ signals to reduce their estimation uncertainty. More specifically, basis functions $$$\{\phi_{r}(t)\}$$$ and coefficient distributions $$$\text{Pr}\left(\{a_{r}\}\right)$$$ were determined from the initial estimate $$$s_{l}(t)$$$ (obtained based on the solutions from Eq. [2]), using PCA analysis and ML-based density estimation, respectively. We then determined the final estimate of the long-$$$\text{T}_{2}^{*}$$$ components in the Bayesian sense:
$$\hspace{13.2em}\min_{a_r}\frac{1}{\sigma^2}\left\lVert{s_{l}(t)-\sum_{r}a_{r}\phi_{r}(t)}\right\rVert_2^2-\log{\text{Pr}\left(\{a_{r}\}\right)}\hspace{13.2em}[4]$$
and removed them from the measured signals. Final MW was determined from the residual by 1-exponential fitting.

Results

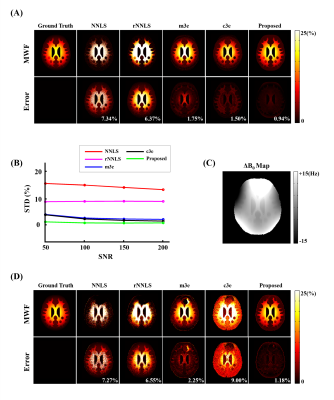
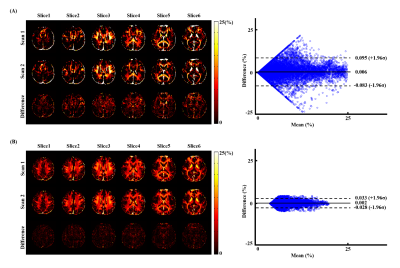
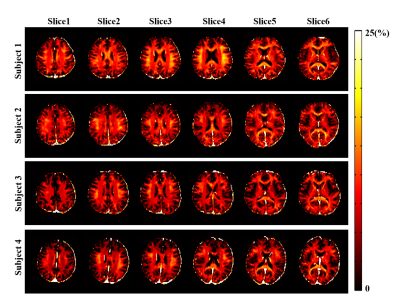
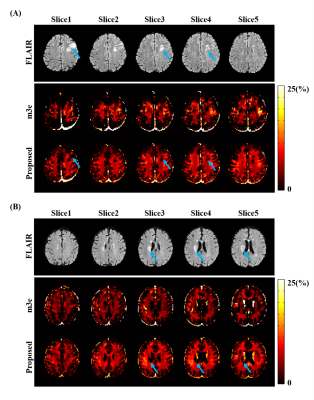
The proposed method has been evaluated using both simulated and in vivo experimental data. In the simulation study, a numerical phantom was generated with parameter values from the literature. We tested the proposed method in the presence of random noise and field-related signal errors, respectively, and compared it with several conventional schemes. The results are summarized in Fig. 1. As can be seen, our model fitted the perturbed signals better than the conventional models. Moreover, our method significantly reduced the noise and field-induced fluctuations and produced more reliable and robust estimation.

In our in vivo experiments, $$$\text{T}_2^*$$$-weighted images were acquired on a 3T scanner using a multi-echo gradient echo (mGRE) sequence. Figure 2 shows the results from one healthy subject. As can be seen, the proposed method showed superior performance over the conventional schemes, with reduced estimation fluctuations, especially in handling the region with large susceptibility effects. To evaluate estimation reproducibility, we compared the MWF values obtained from repeated scans. As shown in Fig. 3, the proposed method achieved significantly reduced inter-scan variations than the conventional methods. The MWF maps obtained from other healthy subjects are summarized in Fig. 4. The proposed has also been applied to data acquired from ischemic stroke patients. As shown in Fig. 5, our method successfully captured the local lesions without significant image artifacts, in contrast to the conventional m3e fitting which failed to detect the myelin loss in the lesions.

Conclusions

We present a new method for robust MWF mapping from $$$\text{T}_2^*$$$-weighted imaging data, which uses an improved signal model, incorporating both learned prior parameter distributions and low-rank signal structures. The proposed method has been validated using both simulated and experimental data, demonstrating superior performance to the conventional multi-exponential fitting schemes. The proposed method may enhance the practical usefulness of MWF mapping in neuroimaging study.

Acknowledgements

This work reported in this paper was supported, in part, by NIH-R21-EB023413, NIH-P41-EB022544 and NIH-U01-EB026978.