0730
BigBrain-MR: a computational phantom for ultra-high-resolution MR methods development1Systems Division, Swiss Center for Electronics and Microtechnology (CSEM), Nêuchatel, Switzerland, 2Medical Image Analysis Laboratory (MIAL), Center for Biomedical Imaging (CIBM), Lausanne, Switzerland, 3Signal Processing Laboratory (LTS5), École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 4Department of Radiology, Centre Hospitalier Universitaire Vaudois (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland
Synopsis
With the increasing importance of ultra-high field systems, suitable simulation platforms are needed for the development of high-resolution imaging methods. Here, we propose a realistic computational brain phantom at 100μm resolution, by mapping fundamental MR properties (e.g., T1, T2, coil sensitivities) from existing brain MRI data to the fine-scale anatomical space of BigBrain, a publicly-available 100μm-resolution ex-vivo image obtained with optical methods. We propose an approach to map image contrast from lower-resolution MRI data to BigBrain, retaining the latter’s fine structural detail. We then show its value for methodological development in two applications: super-resolution, and reconstruction of highly-undersampled k-space acquisitions.
Introduction
With the rapidly growing availability and value of ultra-high field systems, it becomes increasingly relevant to have suitable simulation platforms for the development and optimization of high-resolution imaging methods. A number of fine-scale MRI datasets are publicly available, but with relatively limited resolution (~300μm) and varying incidence of artifacts (e.g. motion, breathing).1,2 Recently, an extremely detailed dataset named BigBrain was obtained from an ex-vivo brain using optical imaging, and made available in digitized format at 100μm isotropic resolution.3 This image offers unprecedented structural detail, yet its histological staining contrast does not directly correspond to fundamental MR properties. The aim of this project is to create a realistic computational brain phantom at 100μm to support the development and assessment of MR methods, by mapping fundamental MR properties (e.g., T1, T2, coil sensitivity fields) from existing brain MRI data to the fine-scale anatomical space of BigBrain. In this first report, we propose a contrast mapping approach and illustrate its application to a T1-weighted (T1w) dataset, to obtain a “T1w-like” BigBrain contrast. Subsequently, we show its value in two applications of high-resolution imaging: (1) super-resolution imaging based on low-resolution acquisitions,4,5 and (2) parallel imaging reconstruction of high-resolution, highly-undersampled k-space data.6Methods
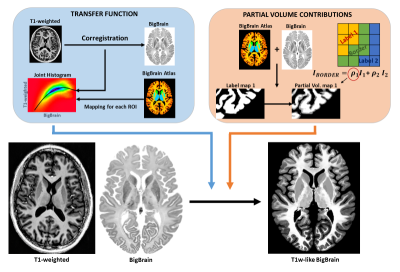
Data: The BigBrain dataset3 included the histological image and a label mask identifying various structures, in MNI space. The label mask was combined with an anatomical atlas from Johns Hopkins University7 to increase the number of labeled sub-cortical structures. The T1w data was acquired from a healthy adult (MP2RAGE8, 0.85mm isotropic resolution, TR/TI1/TI2 = 6000/700/1600ms) using a 7T Magnetom system (Siemens) with a 32-channel receive RF coil (Nova Medical). Ethics approval and written consent were obtained beforehand. The raw data were also processed with ESPIRiT9 to obtain the 32 complex coil sensitivity maps.Contrast mapping to BigBrain: First, the T1w image was registered to BigBrain using a non-linear demons approach (ANTs10). Then, for each region of the label atlas (e.g., cortex, thalamus, putamen), the voxel intensity correspondence between the co-registered T1w and BigBrain was approximated by a 3rd-degree polynomial fit of their joint histogram. For voxels at region borders, a partial volume model was computed to attribute a realistic combination of intensities from the neighboring regions (Fig.1)
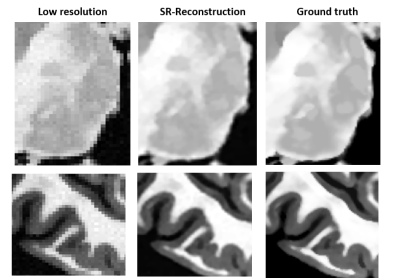
Application 1 – Super-resolution reconstruction: The T1w-like BigBrain was used to assess the performance of a super-resolution technique based on n lower-resolution acquisitions of the same object4,5, with different rotations. To simulate the low-resolution acquisitions (forward model), the T1w-like brain (at 400μm) was rotated on the axial plane (0–45°), followed by blurring (mean filter), downsampling (2×) and noise addition (SNR=10). The underlying 400μm image x was estimated by minimizing: $$E(x)=\frac{1}{2A}\sum_{k=1}^n‖Y_K-H_K x‖_2^2 +\frac{λ}{B}TV(x)$$
where Hk represents each of the n transformations, Yk the low-resolution images, A and B are normalization factors, TV a regularization term (total variation)4,5, and λ the TV weighting factor.
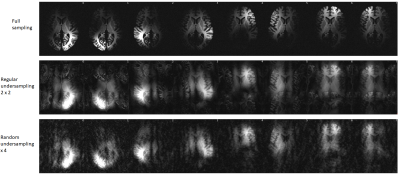
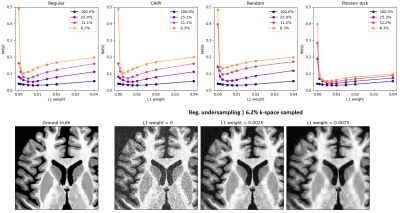
Application 2 – Parallel imaging reconstruction: We simulated a 3D acquisition of the T1w-like BigBrain at 400μm, at 7T with 32 receive channels, with varying types of k-space undersampling, and studied the performance of a wavelet-regularized SENSE reconstruction approach to recover the underlying image. Different undersampling schemes were tested (regular, CAIPI, random, Poisson disk), with varying acceleration (1, 2×2, 3×3, 4×4), and a fixed number of reference lines (8) fully sampled at the center of k-space. The SENSE reconstruction was implemented by minimizing: $$E(x)=\frac{1}{2} ‖PFSx-y‖_2^2+λ‖Wx‖_1$$
with P the sampling operator, F the Fourier transform operator, S the SENSE operator, W the wavelet transform operator, y the (undersampled) k-space measurements, and x the desired image.
Results
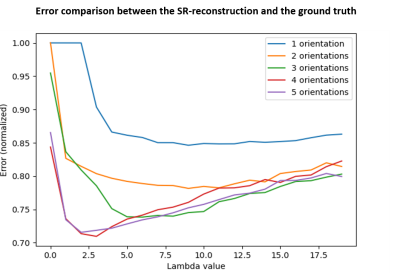
As expected, the mapping approach produced a “T1w-like” image exhibiting fine structural detail and sharpness at the scale of the original BigBrain, with a contrast that closely followed the in-vivo T1w data (Fig.1-bottom). Importantly, by design, this approach was less effective in regions where the T1w showed visible anatomical features but BigBrain did not, or vice-versa (e.g., putamen, caudate nuclei). The simulation framework implemented for super-resolution was found effective, with the approach yielding clearly sharper images than the multi-orientation low-resolution acquisitions, visibly similar to the ground truth (Fig.2). In line with prior expectations, the root-mean-squared error (RMSE) with respect to the ground truth decreased when increasing the number of orientations used for reconstruction; the importance of regularization rose with the number of orientations, while at the same time the optimal λ became smaller (Fig.3). The simulated k-space undersampled acquisitions exhibited realistic undersampling artifacts and dependence on the receive coil sensitivities (Fig.4). Across all reconstruction tests, the RMSE increased with the acceleration factor; the L1 regularization had an increasing impact with increasing acceleration, although at the same time with an increasingly smaller optimal λ (Fig.5-top). The RMSE curve behavior was confirmed to effectively represent the effect of insufficient/appropriate/excessive regularization (Fig.5-bottom).Conclusion
The tests conducted in this first report suggest that our contrast mapping approach can effectively produce a BigBrain-based MRI computational phantom with realistic properties and behavior. Going forward, this approach will be applied to quantitative maps (T1, T2, T2*, etc.), to build a comprehensive simulation platform at 100μm resolution, which may prove highly useful for high-resolution methods development.Acknowledgements
This work was funded by the Swiss National Science Foundation (SNSF) through grant PZ00P2_18590, and supported by the Swiss Center for Electronics and Microtechnology (CSEM), the Center for Biomedical Imaging (CIBM) and the University Hospitals of Lausanne (CHUV).References
(1) Luesebrink F, Hendrik M, Yakupov R, Oeltze-Jafra F, Speck O. The human phantom: Comprehensive ultrahigh resolution whole brain in vivo single subject dataset. Annual ISMRM meeting 2020, Montreal, Canada.
(2) Federau C, Gallichan D. Motion-Correction Enabled Ultra-High Resolution In-Vivo 7T-MRI of the Brain. PLoS One. 2016 May 9;11(5): e0154974. doi: 10.1371/journal.pone.0154974. PMID: 27159492; PMCID: PMC4861298.
(3) Amunts K, Lepage C, Borgeat L, Mohlberg H, Dickscheid T, Rousseau M-É, Bludau S, Bazin PL, Lewis LB, Oros-Peusquens AM, Shah NJ, Lippert T, Zilles K, Evans AC. BigBrain: An ultrahigh-resolution 3D human brain model. Science. 2013; 340(6139):1472-1475. doi: 10.1126/science.1235381. PMID: 23788795.
(4) Yue, Linwei & Shen, Huanfeng & Li, Jie & Yuan, Qiangqiang & Zhang, Hongyan & Zhang, Liangpei. (2016). Image super-resolution: The techniques, applications, and future. Signal Processing. 128. 10.1016/j.sigpro.2016.05.002
(5) Khattab, Mahmoud & Zeki, Akram & Alwan, Ali & Badawy, Ahmed & Thota, Lalitha. (2018). Multi-Frame Super-Resolution: A Survey. 1-8. 10.1109/ICCIC.2018.8782382
(6) Lustig, M., Donoho, D. and Pauly, J.M. (2007), Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med., 58: 1182-1195. https://doi.org/10.1002/mrm.21391
(7) Faria AV, Joel SE, Zhang Y, et al. Atlas-based analysis of resting-state functional connectivity: evaluation for reproducibility and multi-modal anatomy-function correlation studies. Neuroimage. 2012;61(3):613-621. doi:10.1016/j.neuroimage.2012.03.078
(8) Marques et al., MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field, NeuroImage 2010
(9) Uecker M, Lai P, Murphy MJ, et al. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990-1001. doi:10.1002/mrm.24751
(10) Avants, Brian & Tustison, Nick & Song, Gang. (2008). Advanced normalization tools (ANTS). Insight J. 1–35.
Figures