0671
Improved dynamic distortion correction for fMRI using single-echo EPI, a fast sensitivity scan and readout-reversed first image (REFILL)
Simon Daniel Robinson1,2,3, Beata Bachrata3,4, Korbinian Eckstein3, Saskia Bollmann1, Steffen Bollmann5, Siegfried Trattnig3, Christian Enzinger2, and Markus Barth5
1Centre for Advanced Imaging, University of Queensland, Brisbane, Australia, 2Department of Neurology, Medical University of Graz, Graz, Austria, 3Department of Biomedical Imaging and Image-guided Therapy, Medical University of Vienna, Vienna, Austria, 4Christian Doppler Laboratory for Clinical Molecular MR Imaging, Medical University of Vienna, Vienna, Austria, 5School of Electrical Engineering and Information Technology, University of Queensland, Brisbane, Australia
1Centre for Advanced Imaging, University of Queensland, Brisbane, Australia, 2Department of Neurology, Medical University of Graz, Graz, Austria, 3Department of Biomedical Imaging and Image-guided Therapy, Medical University of Vienna, Vienna, Austria, 4Christian Doppler Laboratory for Clinical Molecular MR Imaging, Medical University of Vienna, Vienna, Austria, 5School of Electrical Engineering and Information Technology, University of Queensland, Brisbane, Australia
Synopsis
We propose an improved dynamic distortion correction method for fMRI. A fast (4s) multi-echo GE reference scan is used to calculate coil sensitivities and other non-ΔB0-related contributions to coil phase, and one EPI volume in which the readout direction is reversed allows a phase gradient in the readout direction which is specific to EPI to be determined. Knowledge of these quantities allow fieldmaps to be calculated from the phase of each single-echo EPI volume. Reverse-Encoded First Image and Low resoLution reference scan (REFILL) fieldmaps accurately measure ΔB0 as it changes due to motion and respiration.
Introduction
Susceptibility-related distortion in EPI can be corrected using a map of variations in the B0 field, ΔB0, from the phase of a multi-echo reference scan1. However, a single, static fieldmap does not capture temporal changes in ΔB0 due to physiological fluctuations and motion. Recently, a dynamic distortion correction was proposed in which the contributions to the RF coil phase which are unrelated to ΔB0 - the phase offsets ($$$\theta^c_0$$$) - are determined and subtracted from the phase of each single-echo EPI volume in an fMRI time series to generate a field map for each time point2. However, no correction was proposed for the phase gradient in the readout direction, $$$\phi_G$$$, which may be present in EPI due to eddy currents and timing errors3,4. The phase offset determination also required two lengthy gradient-echo reference scans with opposite readout polarities (TA=90s) and entailed spatial unwrapping.The proposed Reverse-Encoded First Image and Low resoLution reference scan (REFILL) dynamic distortion correction for fMRI makes dynamic fieldmapping more accurate, robust and practicable by introducing a correction for readout phase errors, by determining phase offsets using just one 4s reference scan and removing the need for spatial unwrapping in phase offset estimation.
Theory
GE reference scan: In a sequence with bipolar readouts, the phase of the $$$j^{th}$$$ echo is given by $$\theta_j^c=TE_{j}\cdot\gamma\Delta B_0+\theta^c_0+(-1)^j\phi_{G_{GE}}, \ \ \ \ \ [1]$$where $$$\Delta$$$B$$$_0$$$ is the local magnetic field, $$$\theta^c_0$$$ is the phase offset of coil $$$c$$$, which is dominated by the coil sensitivity and $$$\phi_{G_{GE}}$$$ is the readout phase gradient specific to the GE reference scan.
Given a measurement with at least three echoes, if $$$TE_{j}=j\times TE_{1}$$$, $$$\theta^c_0$$$ can be calculated without phase unwrapping3: $$\theta^c_0=2\theta_1^c-\theta_2^c+3\phi_{G_{GE}}$$ and $$$\phi_{G_{GE}}$$$ as $$\phi_{G_{GE}}=(2\theta_2^c-\theta_1^c-\theta_3^c)/4.$$
EPI time series: Using Equation 1 with complex notation to facilitate summation over coils, a dynamic series of fieldmaps can be calculated from the phase of each EPI time point, $$$\theta^c_{t_{i}}$$$: $$\Delta B_{0,t_{i}}=\frac{1}{\gamma \cdot TE_{EPI}}\angle\sum^c (M^c_{t_i})^2 \cdot \exp i({\theta^c_{t_i}-\theta^c_0 + \phi_{G_{EPI}}}), \ \ \ \ \ [2] $$ in which $$$\theta^c_0$$$ is taken from the GE reference scan and the squared magnitude provides coil sensitivity weighting.
In REFILL, $$$\phi_{G_{EPI}}$$$, the readout phase gradient in EPI, is calculated from an EPI volume in which the readout direction has the opposite polarity to the rest of the time-series: $$\phi_{G_{EPI}} =(1/2) \angle\sum^c M^c_{t_1} \cdot M^c_{REFILL} \cdot \exp i(\theta^c_{t_1}-\theta^c_{REFILL}).$$
Methods
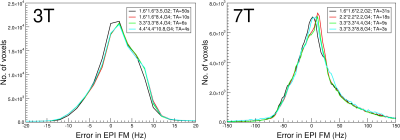
Axial, sagittal and coronal GE and EPI data were acquired with a 3T Siemens PRISMA and a 7T Siemens MAGNETOM scanner with a range of receiver bandwidths and echo times to investigate the behavior of $$$\phi_{G_{GE}}$$$ and $$$\phi_{G_{EPI}}$$$ in vendor sequences.Dynamic fieldmapping of 3 healthy subjects comprised bipolar multi-echo GE reference scans with 3 echoes and a range of resolutions (parameters in Fig.4) and TA ranging from 4s to 50s, followed by a shim change (to mimic the effects of drift, motion and physiology) and EPI with a reverse-encoded first volume (Fig.1). Phase offsets were calculated with ASPIRE3, obviating the need for unwrapping in the online calculations. Offline, fieldmaps were generated from combined, corrected EPI by unwrapping with ROMEO5 and rescaling.
Results
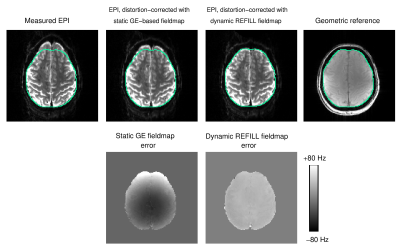
The phase gradient in the readout direction, $$$\phi_{G}$$$, was quite consistent over PE lines but varied with receiver bandwidth and TE (Fig.2). For GE scans it was typically 3 times larger at 3T than at 7T, and for EPI, 25 times larger, with values between 1.1x10-4 rads/mm and 7.5x10-3 rads/mm; the latter being equivalent to 45 Hz across the FOV at 5 ms. The higher values at 3T and opposing trends for 3T and 7T with TE (center) and receiver bandwidth (right) point to sequence timing issues and echo shift corrections rather than eddy currents as the origin.At 3T, fieldmaps generated without correction of $$$\phi_{G_{EPI}}$$$ were subject to error across the image (circa 20 Hz at 3T in the example in Fig.3), which was removed by the REFILL correction, so that EPI-based fieldmaps were accurate to within circa $$$\pm$$$2Hz. Residual discrepancies are attributable to non-linear phase evolution6. At 7T, there was no gradient apparent in EPI fieldmaps, but a constant term which was also removed by REFILL processing.
The accuracy of REFILL fieldmaps was unaffected by the resolution of the reference scans (Fig.4), allowing TA$$$\le$$$4s.
Fig.5 shows that REFILL fieldmaps were also accurate when a shim change was imposed between the reference scans and the EPI (mimicking motion or respiration-related changes in ΔB0), whereas the conventional static GE-based fieldmaps did not capture that change, leading to an imperfect distortion correction (see green contour).
Discussion and Conclusion
We have improved the dynamic distortion correction method proposed by Dymerska et al.2 by i) introducing a correction to remove $$$\phi_{G_{EPI}}$$$, which otherwise introduces errors into fieldmaps ii) replacing the two, dual-echo GE reference scans (TA=90s) by one low-resolution bipolar triple-echo scan (TA=4s) iii) removing the need for phase unwrapping in the online processing steps. REFILL requires just a few seconds of reference scans and one EPI volume with reversed readout direction, totalling circa 6s. If both readout and phase-encode are reversed, the REFILL volume can also be used for TOPUP7. REFILL fieldmaps accurately measure ΔB0 and are insensitive to shim inconsistencies between the reference scans and the fMRI time series.Acknowledgements
This study was funded by the Marie Skłodowska-Curie Action MS-fMRI-QSM 794298. Additional support was provided by the Austrian Science Fund (FWF): 31452. SB and MB acknowledge funding from the NHMRC-NIH BRAIN Initiative Collaborative Research Grant APP1117020, NIH grant 1R01MH111419. The authors acknowledge the facilities and scientific and technical assistance of the National Imaging Facility, a National Collaborative Research Infrastructure Strategy (NCRIS) capability, at the Centre for Advanced Imaging, the University of Queensland.References
1. Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn. Reson. Med. 1995;34:65–73
2. Dymerska B, Poser BA, Barth M, Trattnig S, Robinson SD. A method for the dynamic correction of B0-related distortions in single-echo EPI at 7T. NeuroImage 2018;168:321–331
3. Eckstein K, Dymerska B, Bachrata B, et al. Computationally Efficient Combination of Multi-channel Phase Data From Multi-echo Acquisitions (ASPIRE): Magn. Reson. Med. 2018;79:2996–3006
4. Feng W, Neelavalli J, Haacke EM. Catalytic multiecho phase unwrapping scheme (CAMPUS) in multiecho gradient echo imaging: Removing phase wraps on a voxel-by-voxel basis. Magn. Reson. Med. 2013;70:117–126
5. Dymerska B, Eckstein K, Bachrata B, et al. Phase unwrapping with a rapid opensource minimum spanning tree algorithm (ROMEO). Magn. Reson. Med. 2020 Oct 26. doi: 10.1002/mrm.28563. Epub ahead of print.
6. Wharton S, Bowtell R. Fiber orientation-dependent white matter contrast in gradient echo MRI. Proc. Natl. Acad. Sci. 2012;109:18559–18564
7. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage 2003;20:870–888
Figures
Fig.1: Data acquisition and calculations in
the REFILL approach. A conventional fMRI time-series ('EPI') is
preceded by a low resolution triple-echo GE reference scan, which is
used to calculate (Panel A) phase offsets θ0c and (and a static ΔB0,for
comparison). An EPI volume in which the readout (and optionally the
phase-encode direction) is reversed (see cyan axes in EPI) is used to
calculate the readout-related phase gradient for EPI, φG_EPI
(see Panel B). The calculation of REFILL fieldmaps (Theory section,
Equation 2) was divided into steps to aid reconstruction performance.
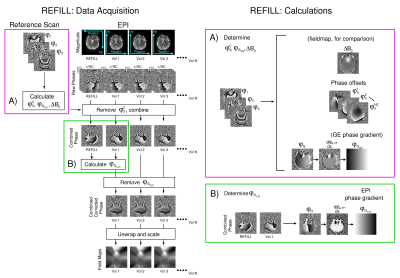
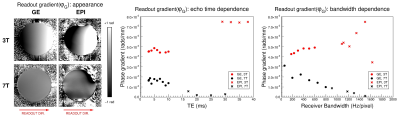
Fig.2: Dependence of the readout gradient, φG, on field strength, sequence, receiver bandwidth and echo time. φG was
close to linear and quite consistent over phase-encode lines (left) and
slices (not shown). It was larger at 3T (red symbols) than 7T (black
symbols) and followed opposing trends with TE and bandwidth at the two
field strengths.
Fig.3: Assessment of the accuracy of EPI-based fieldmaps without and with the REFILL correction. At 3T (left) EPI-based fieldmaps with no additional correction contain both a constant offset and a gradient due to φG_EPI - see phase range in red box and histogram of errors below, which is broad and shifted. The REFILL correction removes both the gradient caused by φG_EPI and the offset. At 7T, the field gradient caused by φG_EPI is too small to be observed, but a constant term is removed by the correction (see phase range and histogram).
Fig 4: The accuracy of EPI-based REFILL fieldmaps is independent of the resolution of the multi-echo reference scans; highly accelerated, low resolution (circa 4-8 mm voxels) reference scans with total acquisition time of 3-4 seconds are sufficient to capture coil sensitivities and yield accurate fieldmaps.
Fig 5: The effect of shim change on the accuracy of a conventional (static) GE-based fieldmap and the dynamic EPI-based REFILL fieldmap. An imposed shim change, mimicking the effect of motion or physiology in fMRI, leads to additional distortion in frontal regions at 7T (top row, left). The change in field is not captured in the static fieldmap, leading to an incomplete correction (second column). The dynamic REFILL fieldmap for this volume is accurate, and gives a complete correction (third column) - see outline transferred from the distortion-free reference (top row, right).