0668

Concomitant field compensation using additional oscillating gradients in a double diffusion encoding imaging sequence

Julian Rauch^1,2, Frederik B. Laun³, Theresa Palm³, Jan Martin^3,4, Maxim Zaitsev^5,6, Mark E. Ladd^1,2,7, Peter Bachert^1,2, and Tristan A. Kuder¹
¹Division of Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, ²Faculty of Physics and Astronomy, Heidelberg University, Heidelberg, Germany, ³Institute of Radiology, University Hospital Erlangen, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, ⁴Division of Physical Chemistry, Lund University, Lund, Sweden, ⁵Medical Physics, Department of Radiology, Faculty of Medicine, Medical Center University of Freiburg, Freiburg, Germany, ⁶High Field Magnetic Resonance Center, Center for Medical Physics and Biomedical Engineering Medical University of Vienna, Vienna, Austria, ⁷Faculty of Medicine, Heidelberg University, Heidelberg, Germany

Synopsis

Concomitant or Maxwell fields cause intravoxel dephasing which can lead to strong image artifacts. In this study, we present a new method for concomitant field correction in double diffusion encoding sequences with single pairs of bipolar gradients on each axis. Additionally implemented oscillating gradients remove the dephasing without changing the desired image. Phase and magnitude images are analyzed with respect to concomitant field induced artifacts and the proposed correction method. We show that the compensation eliminates these artifacts without further consequences for image quality. The method also may be included in other imaging sequences to achieve concomitant field compensation.

Introduction

In diffusion-weighted MRI, strong gradients are usually used to obtain information about diffusion processes within a sample. As a consequence of Maxwell´s equations, these gradients generate concomitant or Maxwell fields, which introduce an additional phase on the transverse magnetization which cannot be rephased as a gradient echo [1, 2].
Diffusion schemes that use single pairs of bipolar diffusion gradients on each axis, being a common double diffusion encoding (DDE) approach [3], are prone to severe artifacts induced by concomitant fields such as signal voids. Unlike the conventional diffusion encoding approach proposed by Stejskal and Tanner [4], these DDE sequences are not intrinsically compensated for intravoxel dephasing induced by concomitant fields.
In this study, we present a novel method for concomitant field compensation in the context of DDE using additional oscillating gradients.

Methods

Experiments were carried out on a SIEMENS Prisma 3T imaging system. A DDE sequence with EPI readout [5] was adapted for concomitant field compensation (Figure 1). Occurring Maxwell fields are given to lowest order by $$\mathrm{B_C(x,y,z,t)} = \frac{1}{2\mathrm{B_0}}(\mathrm{G_x^2z^2+G_y^2z^2+G_z^2\frac{x^2+y^2}{4}-G_xG_zxz-G_yG_zyz}).\qquad(1)$$
$$$\mathrm{B_0}$$$ is the static magnetic field which is modified by the gradients $$$\mathrm{G_x}$$$, $$$\mathrm{G_y}$$$ and $$$\mathrm{G_z}$$$ along the physical scanner axes $$$\mathrm{x}$$$, $$$\mathrm{y}$$$ and $$$\mathrm{z}$$$, respectively. At the isocenter, the concomitant fields are zero.
The concomitant phase results from $$\mathrm{\phi_C(x,y,z)=\gamma\int B_C(x,y,z,t)\,dt},\qquad(2)$$ where $$$\gamma$$$ is the gyromagnetic ratio.
Oscillating gradients were implemented such that the compensation condition $$\mathrm{\int_0^{TE}s_n(t)\,G(t)^2\,dt =0}\qquad(3)$$ is fulfilled, with $$$\mathrm{TE}$$$ being the echo time and $$$\mathrm{s_n(t) = (-1)^{n_{rf}(t)}}$$$, where $$$\mathrm{n_{rf}(t)}$$$ is the number of refocusing pulses within time $$$\mathrm{t}$$$ and $$$\mathrm{TE}$$$.
Since concomitant phase compensation of one axis is done concurrently with diffusion encoding along the second axis, theoretically no increase of the echo time is required.

A water phantom with a length of 30 cm was used in all measurements. Coronal slices were acquired. The phantom center coincided with the isocenter of the scanner. The field-of-view was 350 mm with a matrix size of 128×128. Phase encoding direction was along the $$$\mathrm{x}$$$-axis. The maximum gradient strength was $$$\mathrm{G_x}$$$ = 70 mT/m for both diffusion and oscillating gradients. Durations of the diffusion-weighting gradients were constant at $$$\mathrm{\delta}$$$ = 15.3 ms. The compensation gradients had an oscillation period of 4.2 ms and 14 oscillations giving rise to a maximum $$$\mathrm{b}$$$-value of 14 s/mm².
Acquired values for $$$\mathrm{q=(2\pi)^{-1}\gamma\delta G}$$$ ranged from 0 mm^-1 to 46 mm^-1 yielding $$$\mathrm{b}$$$-values from 0 s/mm² to 900 s/mm² with the bipolar diffusion-weighting gradients. For this proof of concept demonstration, diffusion-weighting and compensation gradients were only applied along the $$$\mathrm{x}$$$-axis.

To quantify the effect on the image phase, measurements using one channel of the integrated Tx/Rx body coil were carried out. Echo time was set to $$$\mathrm{TE}$$$ = 225 ms. Both uncompensated and compensated images were acquired.

Magnitude images were also acquired using a flexible 18-channel body array coil combined with the spine array and the following parameters: Parallel imaging (GRAPPA, acceleration factor 2), phase partial Fourier factor 5/8, receiver bandwidth 1954 Hz/pixel, $$$\mathrm{TE}$$$ = 150 ms.

Results

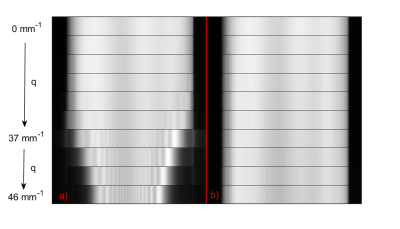
The comparison of the phase behavior for both the compensated and uncompensated acquisitions is shown in Figure 2. Phase values were evaluated within a small region-of-interest (RoI). Without the oscillating gradients, the phase exhibits a parabolic dependency on the $$$\mathrm{q}$$$-value as predicted by Eqs. (1) and (2). A reference curve based on the distance of the RoI from the isocenter is also depicted in Figure 2. Experiment and theory show a high degree of accordance. With the compensation, the phase remains mainly constant and no influence of concomitant fields is observed.

Figure 3 shows the occurrence of the signal voids induced by the concomitant fields in the elongated phantom by displaying representative signal profiles along the $$$\mathrm{z}$$$-axis. The signal was corrected for diffusion attenuation beforehand. As depicted in (a), beginning with $$$\mathrm{q}$$$ = 37 mm^-1, the displayed phantom profiles show severe signal attenuations. Due to the $$$\mathrm{z^2}$$$-dependency of the concomitant field (see Eq. (1)), artifacts worsen with distance from the isocenter. As seen in (b), the oscillating gradients remove the concomitant phase and no related artifacts are visible.

In Figure 4, uncompensated and compensated magnitude images acquired with $$$\mathrm{q}$$$ = 46 mm^-1 are shown together with a reference image ($$$\mathrm{q}$$$ = 0 mm^-1). The full image in (a) again highlights the artifacts which are removed in (b).

Discussion and Conclusion

It could be shown that the usage of oscillating gradients is an efficient tool for the removal of concomitant field induced artifacts in the frame of DDE. Phase and magnitude were no longer affected by the concomitant phase induced by the bipolar diffusion gradient pairs. The oscillating gradients generated a negligible diffusion weighting of 1.6 % of the acquired $$$\mathrm{b}$$$-value. Thus, the desired diffusion image was well conserved.
In order to null the resulting concomitant phase, a sufficient number of gradient oscillations with adequate strength and duration must be used which might exceed the stimulation limit.

Ongoing research includes the usage of concomitant field compensation with simultaneous diffusion weighting on the same axis.
In conclusion, the proposed method can enhance image quality whenever large gradient strengths and field-of-views cause concomitant field-related artifacts in DDE.

Acknowledgements

No acknowledgement found.

References

[1] Bernstein MA et al. Concomitant gradient terms in phase contrast MR: analysis and correction. Magn Reson Med. 1998;39(2)

[2] Szczepankiewicz F et al. Maxwell-compensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding. Magn Reson Med. 2019;82(4)

[3] Shemesh N et al. Conventions and nomenclature for double diffusion encoding NMR and MRI. Magn Reson Med. 2016;75(1)

[4] Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 1965;42(1)

[5] Martin J et al. Contrast-to-noise ratio analysis of microscopic diffusion anisotropy indices in q-space trajectory imaging. Z Med Phys. 2020;30(1)

Figures

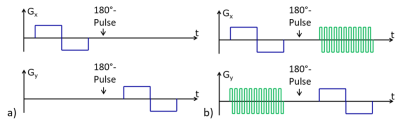
Figure 1: Schematic representation of the proposed method in a spin-echo double diffusion encoding sequence. a) Bipolar diffusion-weighting gradients (blue) are used for double diffusion encoding, here for instance along the physical x and y axes. These gradients induce additional concomitant fields which cause severe artifacts. b) Oscillating gradients (green) are implemented to null the concomitant fields induced by the bipolar gradients.

Figure 2: Phase behavior averaged over a RoI. The phase at q = 0 mm^-1 was set to zero. Without compensation, the expected parabolic dependency on the gradient strength, i.e. on the q-value, is visible (blue). A theoretical reference curve (red) was calculated using the distance of the RoI from the scanner isocenter. Experiment and reference exhibit high accordance. With compensation, the phase remains mainly constant (black).

Figure 3: Phantom magnitude along the physical z-axis for increasing q-values. A band of 30 pixels within the phantom was averaged to obtain the shown length representations. a) Severe signal attenuations occur under the influence of concomitant fields. Due to the z²-dependency of the concomitant phase, the phantom seems to shrink. b) The compensation with the oscillating gradients removes the concomitant phase and related artifacts, no signal attenuations can be noted.

Figure 4: Comparison of acquired magnitude images for the long phantom cylinder orientated along the z-axis. The images were corrected for diffusion attenuation. a) Without concomitant field compensation, the image exhibits strong artifacts, especially signal voids (q = 46 mm^-1). b) No concomitant field related artifacts can be seen when the concomitant phase is removed by the oscillating gradients (q = 46 mm^-1). c) Image acquired with q = 0 mm^-1 as reference.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0668