Introduction

The apparent diffusion coefficient (ADC) slightly varies in brain tissue over the cardiac cycle^1,2. Various physiological reasons have been proposed to explain the observed variation, including glymphatic clearance activity of the brain³. Yet, it is known from cardiac diffusion imaging that tissue strains also induce artificial ADC variations^4,5. In this study, we introduce a high-field magnetic resonance imaging (MRI) sequence with stimulated echo acquisition mode (STEAM) to simultaneously measure brain tissue strain and ADC. We utilize the sequence to investigate to what extent ADC variations over the cardiac cycle can be explained by strain-induced measurement errors.

Theory

Diffusion MRI encodes molecular diffusion effects in the NMR signal by using bipolar gradient pulses. However, tissue deformation during the course of the measurement leads to a modified spatial frequency⁴
$$k'=\frac{k_{0}}{(1+S)}$$
where S is the strain along the encoding direction and $$$k_{0}=2\pi\gamma{G}\delta$$$. After the second gradient lobe, the stimulated echo signal $$$M_{T}$$$ over a given voxel is given by
$$M\left(x\right)=\frac{M_{0}}{2}\exp{\left(ix\left(k'-k_{0}\right)\right)}\exp{\left(-bD_{obs}\right)}$$
Here, $$$D_{obs}$$$ is the observed diffusion coefficient that is different from the ‘true’ ADC because the modified spatial frequency induces a different effective b-value at the tissue level, even if the tissue is in the undeformed state during readout again⁴. This phenomenon was already described by Reese et al⁴:
$$D_{obs}=\frac{D}{\Delta}\int_{0}^{\Delta}\frac{1}{(1+S(t))}dt=\frac{D}{S+1}$$
where we assumed that S increases linearly over the mixing time $$$\Delta$$$ (e.g. constant strain rate: $$$S(t)=\frac{S\cdot{t}}{\Delta}$$$. Eq. 3 shows that the observed diffusion coefficient reduces for positive strain and increases for negative strain. The additional term $$$\exp{(ix(k'-k_{0}))}$$$ in Eq. 2 quantifies the phase dispersion as a result of imperfect refocusing of the signal in deformed tissue. If we assume that the phase induced by the strain is static during the readout ($$$\delta<<\Delta$$$), the measured signal in the deformed state of that voxel yields
$$M_{d}=\frac{M_{0}}{2}\exp{\left(-bD_{obs}\right)}\int_{0}^{d}\exp{\left(ix\left(k'-k_{0}\right)\right)dx}$$
The magnitude of the signal is then given by
$$\begin{align*}|M_{d}|&=\left(\frac{M_{0}}{k'-k_{0}}\right)\left|\sin\left(\frac{d}{2}\left(k'-k_{0}\right)\right)\right|\exp{(-bD_{obs})}\\&\approx\frac{M_{0}}{2}\left(d-\frac{d^{3}}{6}\left(k'-k_{0}\right)^{2}\right)\exp{(-bD_{obs})}\end{align*}$$

Methods

We developed a single-shot multi-slice STEAM MRI sequence that simultaneously captures both strain-rate and ADC of brain tissue with full brain coverage over the cardiac cycle. The approach can be regarded as either a slice-selective single-shot multi-slice DENSE^6,7 sequence or a stimulated echo (STE) diffusion sequence (Figure 1). The sequence enables us to simultaneously obtain diffusion weighted images and velocity images from the magnitude and phase data, respectively.

Written informed consent was obtained from 8 healthy volunteers (4 females, age 25±4 years (mean±std)) in accordance with the Ethical Review board of our institution. The volunteers were scanned at 7T (Philips Healtcare) using an 8-channel transmit and 32-channel receive head coil (Nova Medical). For each subject, DENSE measurements were obtained with sagittal orientation and in-plane Feet-to-Head (FH) motion/diffusion encoding. The DENSE series consisted of 52 non-triggered repeated scans, half of the scans with b=300s/mm² (k₀=56mm^-1) and the other half with b=1000s/mm² (k₀=102mm^-1). The mixing time $$$\Delta$$$ was set to 100ms, with limited signal loss due to relaxation effects (predominantly determined by T1 instead of T2). Alternating encoding polarities were applied to distinguish between motion induced phase and phase confounders (equivalent v_enc=0.51/0.28mm/s for b=300/1000s/mm², respectively). Further imaging parameters included 72 slices; SENSE: 2.6 (AP direction); resolution: 3x3x3mm³; FOV: 240x240x216mm³; single-shot EPI (factor: 35); TE/2: 24ms; TR: 7.5s. Physiological data from a pulse-oximeter (POx) was simultaneously recorded to measure the cardiac interval position. A T1-weighted turbo field echo (TFE) scan (resolution: 1.00x1.00x1.00 mm³; FOV 250x250x190 mm³) was acquired as anatomical reference.

DENSE magnitude data was used for rigid image registration with Elastix⁸ (Figure 2). Since adjacent slices were acquired at different positions in the cardiac cycle, only in-plane degrees of freedom were used for registration. Transformation was applied to the complex data. Tissue strain rates were obtained by computing the spatial derivative along the encoding direction followed by unwrapping under the assumption of small strain rates $$$\left(S<<\frac{v_{enc}}{\Delta{x}}\right)$$$. The data was interpolated over the cardiac cycle to obtain 10 cardiac phases. Positive and negative encoded strain rate data was interpolated separately and subtracted to eliminate static confounders. Similarly, b=300 and b=1000 magnitude data were interpolated separately, after which ADC maps were fitted. Cardiac phases were shifted such that peak systolic strain-rate occurred at 20% of the cardiac interval.

The T1-weighted data was registered to the DENSE data and segmented. A conservative white matter tissue mask was created, by discarding voxels with CSF probability larger than 0, and additional city-block erosion to assure no partial volume effects from blood and CSF.

Results

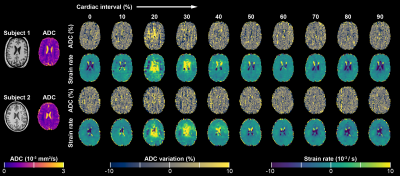
We present the preliminary results from 2 subjects (#1: male, age 27; #2: female, age 25). Average ADC values in the mask were 7.14·10^-4 and 7.12·10^-4mm²/s, for these subjects, respectively. Strain rates and ADC ratio fluctuations showed good correlation (R=0.92 and R=0.80, respectively). Measured ADC fluctuation over the cardiac cycle was about an order of magnitude larger than predicted by ‘worst case’ calculation (range: 4.5% versus 0.49% and 3.0% versus 0.35% for the subjects, respectively). Table 1 represents the error in the measured ADC as function of strain and true ADC.

Discussion and Conclusion

The results show that the impact of tissue strain on the ADC is too small to explain the observed fluctuation over the cardiac cycle. As only b values larger than 300 were included, the fluctuations likely do not reflect blood flow pulsations.

Acknowledgements

The research leading to these results was supported by Vici Grant 918.16.616 from the Netherlands Organization for Scientific Research (NWO) awarded to Geert Jan Biessels and the European Union’s Horizon 2020 research and innovation program under grant agreement no. 666881, SVDs@target.