0647

Estimation of intra-axonal axial diffusivity by tensor-valued dMRI and powder-averaging

Markus Nilsson¹, Samuel St-Jean^1,2, Christian Beaulieu², and Filip Szczepankiewicz¹
¹Clinical Sciences Lund, Lund University, Lund, Sweden, ²Department of Biomedical Engineering, University of Alberta, Edmonton, AB, Canada

Synopsis

The intra-axonal axial diffusivity (D_a) has a prominent role in describing and modeling the white matter microstructure, but cannot be obtained from regular diffusion tensor imaging due to the influence of orientation dispersion and extracellular water. It may be estimated using higher b-values and modeling, however, its estimation is still an ill-posed problem or requires knowledge of the orientation distribution function. Here, we show that using b-tensor encoding and powder averaging turns the problem into a well-posed one and allows rapid mapping across the whole brain yielding D_a values of 2.2-2.7 µm²/ms.

Introduction

The “standard model” of white matter (WM) diffusion describes WM microstructure by four key parameters.¹ One of these is the apparent axial diffusivity of intra-axonal water (D_a). However, its value is unknown. NODDI assume it to 1.7 µm²/ms,² consistent with the axial diffusivity from DTI in coherent WM.³ However, the axial diffusivity from DTI is lower than D_a due to orientation dispersion and extracellular water. Howard et al suppressed extra-axonal water by ultra-high b-values and modelled orientation dispersion, and found values between 2.3 and 3.0 µm²/ms.⁴ Lampinen et al used a diffusion-relaxation approach with b-tensor encoding and found values of approximately 1.8 µm²/ms.⁵ Finally, Dhital et al used planar and oblate b-tensors to arrive at a WM average of 2.4 µm²/ms.⁶ Here we present a simple approach for rapid estimation of D_a for whole brain imaging, based on linear and prolate tensor encoding.⁷

Theory

We assume that the diffusion-weighted signal in white matter can be described by a two-compartment model featuring intra and extra axonal water.¹ The intra-axonal compartment is modelled by a diffusion tensor with non-zero D_a but a radial diffusivity of zero. The extra-axonal compartment is assumed to have a non-zero radial diffusivity. Therefore, at sufficiently high b-values, the extra-axonal compartment is fully attenuated, and the remaining intra-axonal signal is described by
$$S~=~S_a~\int\,P({\bf n})\,\exp(-D_a{\bf n}^{\otimes\,2}:\bf{B})\rm{d}\bf{n}$$
with three unknowns: the intra-axonal signal without diffusion encoding – S_a; the axonal fiber orientation distribution function (fODF) – P(n), and the intra-axonal axial diffusivity – D_a. Moreover, B is the diffusion encoding tensor.^7,8
The number of unknown model features is reduced by considering the powder-averaged signal and borrowing theory from previous papers^5,9,10
$$S\,\approx\,S_a\exp(-b[1-b_\Delta]\tfrac{1}{3}D_a)(\tfrac{4}{\pi}b~b_\Delta~D_a)^{-1/2}$$
The approximation is valid when $$$b~b_\Delta~D_a>>1$$$, where $$$b_\Delta$$$ describes the shape of the b-tensor.⁹ Estimation of D_a is degenerate when using only linear b-tensor encoding (LTE, $$$b_\Delta=1$$$), because Eq.2 then reduces to
$$S_\rm{LTE}=S_aD_a^{-1/2}(\tfrac{4}{\pi}b)^{-1/2}$$
with two unknowns but only one experimental parameter to vary. However, complementing the experiment with prolate tensor encoding (PrTE, $$$0<b_\Delta<1$$$) and taking the ratio of the LTE and PrTE signal at identical b-values yields
$$S_\rm{LTE}/S_\rm{PrTE}=\exp(-b[1-b_\Delta]\tfrac{1}{3}D_a)b_\Delta^{1/2}$$
This is trivial to solve, meaning D_a can be mapped with minimal additional assumptions on top of the “standard model”.

Methods

Data was acquired in one healthy volunteer (30–40 years of age) on a 3T MAGNETOM Prisma (Siemens Healthcare, Erlangen, Germany) using a prototype spin-echo pulse-sequence for b-tensor encoding.¹¹ Waveforms rendering linear and prolate b-tensors ($$$b_\Delta$$$ =1 and 0.9) were optimized^12,13 and scaled to yield b = 6 ms/µm². Each b-tensor was rotated along 64 directions. Imaging employed a single-shot 2D EPI with TE/TR=120/2800 ms/ms, and 30 axial slices (5 mm thick) with an in-plane resolution of 2.2×2.2 mm² for a total acquisition time of 7 minutes. Data was denoised using MP-PCA.¹⁴ Voxel-wise values of D_a was estimated via Eq. 4. For comparison, we also investigated fitting both the fODF and axial diffusivity, assuming a Watson-distributed fODF and a free distribution using non-negative least squares fitting. Values of D_a were presented as parameter maps and averaged from ROIs placed in major white matter regions.

To verify the added value of b-tensor encoding, we compared our approach to the LTE-only approach by Howard et al.⁴ Signals were generated assuming a Watson-distributed fODF,² using either the experimental protocol or LTE with b-values of 8, 12, and 16 ms/µm² (as in ref 4). The sum-of-squares distance between the signal generated with an orientation dispersion (OD) of 0.1 and D_a=2.4 µm²/ms and signals generated with different values of D_a and OD were analyzed. Multiple solutions with a sum-of-squares of zero indicates degeneracy.

Results

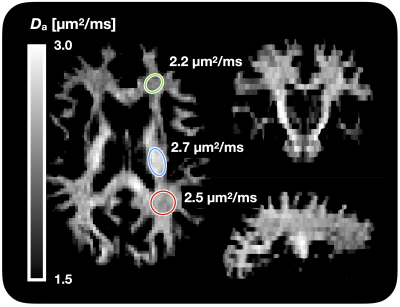
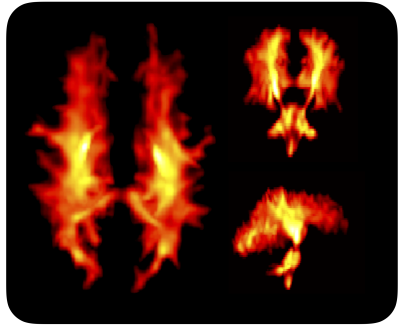
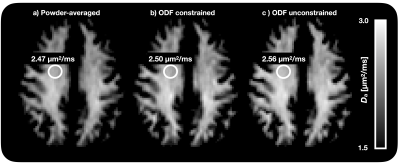
Figure 1 shows D_a estimated from the proposed approach. The value of was 2.7 µm²/ms in the corticospinal tract, 2.5 µm²/ms in the posterior white matter, and 2.2 µm²/ms in the anterior white matter, the latter two both classic fibre crossing regions. Figure 2 shows a maximum-intensity projection with colors adapted to emphasize regions of high D_a. Again, the cerebrospinal tracts exhibit the highest D_a. Figure 3 shows the effect of including constrained and unconstrained fODFs. The similarity across methods indicates that the assumptions on the ODF shape has little influence on estimation. This raises the question of whether fitting a constrained ODF and the axial diffusivity to LTE data would be possible. Unfortunately, Figure 4 shows that the problem is well-posed only if signal is acquired with two b-tensor shapes, whereas it is degenerate for LTE alone.

Discussion

We demonstrated an efficient method for estimation of the purported intra-axonal axial diffusivity. Knowing this parameter is important for avoiding errors in estimates of microstructure parameters. For example, the neurite density provided by NODDI increase by 150% as D_a increased from 1.7 to 3.0 µm²/ms.⁴ Previous approaches utilized only linear diffusion encoding,⁴ which seems to constitute a degenerate problem (Fig. 4) – or planar and oblate encoding⁶ – which is experimentally less efficient than the proposed approach.⁷ We find that D_a is heterogeneous across the brain. This is likely due to variations in axonal morphology,⁴ and occurs around the expected value (2.4–2.5 µm²/ms,¹⁵ rescaled to body temperature). Future work will apply the approach to a wider range of subjects.

Acknowledgements

We thank Siemens Healthcare (Erlangen, Germany) for access to the pulse sequence programming environment.

References

1. Novikov, D. S., Fieremans, E., Jespersen, S. N., & Kiselev, V. G. (2019). Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR in Biomedicine, 32(4), e3998. http://doi.org/10.1002/nbm.3998

2. Zhang, H., Schneider, T., Wheeler-Kingshott, C. A., & Alexander, D. C. (2012). NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage, 61(4), 1000–1016. http://doi.org/10.1016/j.neuroimage.2012.03.072

3. Alexander, D. C., Hubbard, P. L., Hall, M. G., Moore, E. A., Ptito, M., Parker, G. J. M., & Dyrby, T. B. (2010). Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage, 52(4), 1374–1389. http://doi.org/10.1016/j.neuroimage.2010.05.043

4. Howard, A. F., Lange, F. J., Mollink, J., Cottaar, M., Drakesmith, M., Umesh Rudrapatna, S., et al. (2020). Estimating intra-axonal axial diffusivity in the presence of fibre orientation dispersion, biorXiv. http://doi.org/10.1101/2020.10.09.332700

5. Lampinen, B., Szczepankiewicz, F., Mårtensson, J., Westen, D., Hansson, O., Westin, C.-F., & Nilsson, M. (2020). Towards unconstrained compartment modeling in white matter using diffusion‐relaxation MRI with tensor‐valued diffusion encoding. Magn Reson Med, 29, 268–19. http://doi.org/10.1002/mrm.28216

6. Dhital, B., Reisert, M., Kellner, E., & Kiselev, V. G. (2019). Intra-axonal diffusivity in brain white matter. NeuroImage, 189, 543–550. http://doi.org/10.1016/j.neuroimage.2019.01.015

7. Szczepankiewicz, F., Westin, C.-F., & Nilsson, M. (2020). Gradient waveform design for tensor-valued encoding in diffusion MRI. Journal of Neuroscience Methods, 109007. http://doi.org/10.1016/j.jneumeth.2020.109007

8. Westin, C.-F., Knutsson, H., Pasternak, O., Szczepankiewicz, F., Ozarslan, E., van Westen, D., et al. (2016). Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage, 135(C), 345–362. http://doi.org/10.1016/j.neuroimage.2016.02.039

9. Eriksson, S., Lasič, S., Nilsson, M., Westin, C.-F., & Topgaard, D. (2015). NMR diffusion-encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. The Journal of Chemical Physics, 142(10), 104201. http://doi.org/10.1063/1.4913502

10. Veraart, J., Fieremans, E., & Novikov, D. S. (2019). On the scaling behavior of water diffusion in human brain white matter. NeuroImage, 185, 379–387. http://doi.org/10.1016/j.neuroimage.2018.09.075

11. Szczepankiewicz, F., Sjölund, J., Ståhlberg, F., Lätt, J., & Nilsson, M. (2019). Tensor-valued diffusion encoding for diffusional variance decomposition (DIVIDE): Technical feasibility in clinical MRI systems. PLoS ONE, 14(3), e0214238. http://doi.org/10.1371/journal.pone.0214238

12. Sjölund, J., Szczepankiewicz, F., Nilsson, M., Topgaard, D., Westin, C.-F., & Knutsson, H. (2015). Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of Magnetic Resonance (San Diego, Calif : 1997), 261, 157–168. http://doi.org/10.1016/j.jmr.2015.10.012

13. Szczepankiewicz, F., Westin, C.-F., & Nilsson, M. (2019). Maxwell-compensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding. Magn Reson Med. http://doi.org/10.1002/mrm.27828

14. Veraart, J., Novikov, D. S., Christiaens, D., Ades-aron, B., Sijbers, J., & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. NeuroImage, 142, 394–406. http://doi.org/10.1016/j.neuroimage.2016.08.016

15. Beaulieu, C., & Allen, P. S. (1994). Water diffusion in the giant axon of the squid: implications for diffusion-weighted MRI of the nervous system. Magn Reson Med, 32(5), 579–583.

Figures

Fig. 1. Intra-axonal axial diffusivity estimated using the proposed approach. Values were lowest in the anterior white matter (green), intermediate in the posterior white matter (red), and highest in the corticospinal tract (blue).

Fig. 2. Maximum-intensity projections of the intra-axonal axial diffusivity across multiple slices illustrating the elevated values of intra-axonal axial diffusivity found in the corticospinal tract and the brainstem.

Fig. 3. Intra-axonal axial diffusivity estimated in combination with the orientation distribution function, under different assumptions. Panel (a) shows results obtained from the powder average and (b) and (c) with the fODF constrained using the Watson distribution and an unconstrained variant, respectively. Results are in good agreement with each other, although slightly higher for the methods estimating both D_a and the fODF.

Fig. 4. Intra-axonal axial diffusivity estimation is a well-posed problem when using multiple b-tensor shapes but ill-posed when using multiple b-values only. The dark regions show regions where different values of D_a and OD yielded very similar signal curves – i.e. low sum-of-squares differences to the one generated with the ground-truth values (red dot).

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0647