0645
Feasibility of axon diameter estimation in complex fiber architectures by powder averaging of the diffusion MRI signal1Danish Research Centre for Magnetic Resonance, Hvidovre, Denmark, 2Technical University of Denmark, Kgs. Lyngby, Denmark, 3Signal Processing Laboratory (LTS5), École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
Synopsis
Orientation dispersion bias in axon diameter measurements can be removed by powder averaging of the diffusion MRI signal in isotropically distributed directions, but has not been validated in complex fiber architectures. Here, we demonstrate the success of the spherical mean technique (SMT) and a recent power law (PL) implementation in removing orientation-related bias in diameter estimates of real axons from the splenium corpus callosum and a complex crossing fiber region of the vervet monkey brain. In the crossing fiber region, we find a significant population of very large axons, indicating a need for sensitivity to a wide range of diameters.
Introduction
Axonal conduction velocity depends on axon diameter (AD)1, making AD an indicator of white matter (WM) performance. Diffusion MRI enables noninvasive AD estimation2–4, but axonal orientation dispersion (OD)5–7 causes an overestimation of AD2,3,8. ActiveAx3 accounts for unknown fiber orientation, but not OD. Other approaches attempt to model the OD9, but place limits on its functional form.Recent work disentangles AD from the OD10–12 by powder averaging (PA) of the diffusion MRI signal. In-vivo AD estimation has been demonstrated with different approaches. Fan et al.13, implement a multi-compartment spherical mean technique (SMT) approach, while Veraart et al.14 model the intra-axonal space (IAS) by fitting a power law (PL) to the PA signal at high b-values. In Monte Carlo (MC) simulations within the realistic IAS of the mouse corpus callosum (CC)5, the PL implementation removed OD bias at short diffusion times. However, the performance of PA-based AD estimates has not yet been validated in more complex WM regions.
Here, we demonstrate the success of the SMT and PL in removing OD bias from the AD estimates of axons from a CC and crossing fiber region of the primate brain, while highlighting the need for sensitivity to the wide range of ADs that can be found at subvoxel scales.
Methods
Axon segmentation and analysisThe axons originate from the brain of a 32-month female vervet monkey, imaged with 3D synchrotron x-ray nano-holotomography (XNH) at the European Synchrotron Research Facility6. A description of both XNH volumes, and the segmentation/analysis of splenium axons is given in Andersson et al6. The crossing fiber axons were similarly processed. The volume-weighted AD, $$$d$$$, of each axon was estimated as $$$d=\sum_{i=1}^{N}2r_i\cdot\left(\frac{\pi r_i^2}{\sum_{i=1}^{N}\pi r_i^2}\right)$$$ where $$$r_i$$$ is the $$$i$$$th measured radius of $$$N$$$ equidistant measurement points along the axonal trajectories.
MC simulations
The Monte Carlo Diffusion and Collision (MCDC) framework15 was used to simulate diffusion within each axon using an intrinsic diffusivity of $$$D_0 = 0.6\cdot10^{-9}$$$ m2/s, $$$2\cdot10^5$$$ uniformly distributed spins and $$$1\cdot10^{-5}$$$ seconds per timestep, as in Andersson et al6. Three pulsed-gradient spin echo (PGSE) sequences with gradient duration $$$\delta=7$$$ ms, gradient separation $$$\Delta=30$$$ ms, gradients $$$G=[500,600,700]$$$ mT/m and $$$b=[24.3,34.9,47.5]$$$ ms/mm2 were simulated in 30 isotropically distributed directions.
Analytical diffusion MRI signal from cylinders
Using the PGSE parameters above, the signal perpendicular to 75 cylinders of diameter 0.2 to 15.0 µm (0.2 µm intervals), $$$S_{\perp}$$$, was calculated with Eq.11 from Van Gelderen et al.16. The perpendicular apparent diffusion coefficient (ADC), $$$D_{\perp}$$$, was subsequently calculated from $$$\ln{S_{\perp}}=-bD_{\perp}$$$, and the ADC in direction $$$\mathbf{G}=[G_x,G_y,G_z]$$$ as:
$$ADC=\mathbf{G}\times\begin{pmatrix}D_{\parallel} & 0 & 0\\0 & D_{\perp} & 0\\0 & 0 & D_{\perp}\end{pmatrix}\times\mathbf{G’}\tag{1}$$
where $$$D_{\parallel}$$$ is the cylinder axial diffusivity. The signal along the 30 directions was calculated from the ADCs.
Power law AD estimation
Using the nonlinear least squares estimator provided by Veraart and Novikov17, the PL formulation in Veerart et al.14 was fitted to the PA signal, $$$\overline{S}(b)$$$, of each axon:
$$\overline{S}(b)=\beta\exp^{-bD_{\perp}}b^{-0.5}\tag{2}$$
providing $$$D_{\perp}$$$ and a parameter, $$$\beta$$$. The Neuman assumption of the long-pulse limit and intrinsic diffusivity $$$D_0=0.6\cdot10^{-9}$$$ m/s were used to convert $$$D_{\perp}$$$ into a diameter estimate14.
SMT AD estimation
Analytically, the PA signal in a cylinder is18:
$$\overline{S}(b)=f_{IAS}\left( \exp^{-bD_{\perp}}\cdot\sqrt{\frac{\pi}{4b\cdot(D_{\parallel}-D_{\perp})}} \cdot\Phi(\sqrt{ b\cdot (D_{\parallel}-D_{\perp})}\right)\tag{3}$$
where $$$\Phi(x)$$$ is the error function of $$$x$$$ and $$$f_{IAS}$$$ is the IAS signal fraction. A Levenberg-Marquardt fit of Equation 3 to $$$\overline{S}(b)$$$ gave estimates of $$$f_{IAS}$$$ and $$$D_{\perp}$$$. Contrary to the PL, a fixed $$$D_{\parallel}=D_0$$$ was assumed. $$$D_{\perp}$$$ was converted to AD using Eq.11 from Van Gelderen et al.16.
Results and Discussion
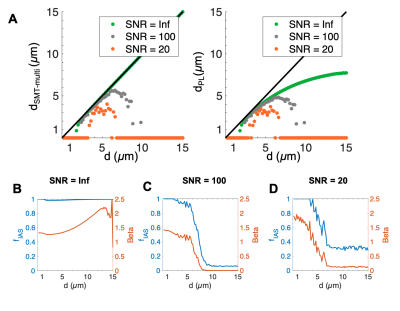
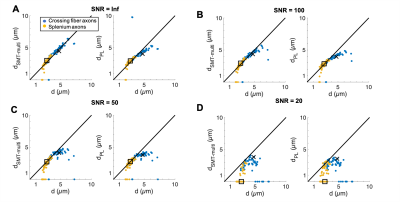
The segmented crossing fiber axons (Figure 1B) were significantly larger than those of the splenium (Figure 1A). They showed more variability in morphology, having volume-weighted mean ADs up to 7 µm and tortuous trajectories of lengths up to 313 µm.In cylinders, the SMT technique accurately estimated diameter and $$$f_{IAS}$$$ (equal to 1) for diameters >~1.5 µm at infinite SNR (Figures 2A-B). For infinite SNR, the PL gave a similar lower bound of measurable diameter, but underestimated larger diameters as the heavily attenuated PA signal was attributed to a change in $$$\beta$$$, and not only reduced $$$D_{\perp}$$$. For both approaches, the addition of Rician signal noise shifted the lower bound to larger diameters and caused an underestimation of diameter, especially at large diameters.
Aside from at SNR 20 where fitting failed, both techniques accurately estimated the volume-weighted mean AD of the splenium axon population, but tended to underestimate the crossing fiber mean AD. Underestimation is caused by i) noise (even at infinite SNR, MC simulations have some noise), ii) for the SMT – the assumption that $$$D_{\parallel}=D_0$$$, which we and others have shown is not the case5–7 and iii) for the PL, difficulty in fitting both $$$D_{\perp}$$$ and $$$\beta$$$. Also, although $$$D_{\parallel}$$$ is not assumed in the PL fit, this approach is not void of assumptions since a value of $$$D_0$$$ is required to convert $$$D_{\perp}$$$ into AD.
Conclusion
The study of the crossing fiber region revealed a significant population of very large axons (~4-7 µm), indicating a need for sensitivity to a wide range of ADs with diffusion MRI. Despite their extremely nonuniform morphologies, PA techniques accurately estimated the volume-weighted ADs of the splenium CC and crossing fiber axons given sufficient SNR.Acknowledgements
MA, HMK were supported by the Capital Region Research Foundation (grant number: A5657) (PI:TD). This work has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 75446 (MP). HL has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 804746).References
1. Hursh, J. B. CONDUCTION VELOCITY AND DIAMETER OF NERVE FIBERS. American Journal of Physiology-Legacy Content 127, 131–139 (1939).
2. Dyrby, T. B., Sogaard, L. V., Hall, M. G., Ptito, M. & Alexander, D. C. Contrast and stability of the axon diameter index from microstructure imaging with diffusion MRI. Magn. Reson. Med. 70, 711–721 (2013).
3. Alexander, D. C. et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage 52, 1374–1389 (2010).
4. Assaf, Y., Blumenfeld-Katzir, T., Yovel, Y. & Basser, P. J. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn. Reson. Med. 59, 1347–1354 (2008).
5. Lee, H.-H. et al. Along-axon diameter variation and axonal orientation dispersion revealed with 3D electron microscopy: implications for quantifying brain white matter microstructure with histology and diffusion MRI. Brain Struct. Funct. 224, 1469–1488 (2019).
6. Andersson, M. et al. Axon morphology is modulated by the local environment and impacts the non-invasive investigation of its structure-function relationship. Proc. Natl. Acad. Sci. U. S. A. In Press.
7. Lee, H.-H., Jespersen, S. N., Fieremans, E. & Novikov, D. S. The impact of realistic axonal shape on axon diameter estimation using diffusion MRI. Neuroimage 223, 117228 (2020).
8. Barazany, D., Basser, P. J. & Assaf, Y. In vivo measurement of axon diameter distribution in the corpus callosum of rat brain. Brain 132, 1210–1220 (2009).
9. Zhang, H., Hubbard, P. L., Parker, G. J. M. & Alexander, D. C. Axon diameter mapping in the presence of orientation dispersion with diffusion MRI. Neuroimage 56, 1301–1315 (2011).
10. Kaden, E., Kruggel, F. & Alexander, D. C. Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magn. Reson. Med. 75, 1752–1763 (2016).
11. Kaden, E., Kelm, N. D., Carson, R. P., Does, M. D. & Alexander, D. C. Multi-compartment microscopic diffusion imaging. Neuroimage 139, 346–359 (2016).
12. Pizzolato, M., Wassermann, D., Deriche, R., Thiran, J.-P. & Fick, R. Orientation-Dispersed Apparent Axon Diameter via Multi-Stage Spherical Mean Optimization. in Computational Diffusion MRI 91–101 (Springer International Publishing, 2019).
13. Fan, Q. et al. Axon diameter index estimation independent of fiber orientation distribution using high-gradient diffusion MRI. Neuroimage 222, 117197 (2020).
14. Veraart, J. et al. Nonivasive quantification of axon radii using diffusion MRI. Elife 9, (2020).
15. Rafael-Patino, J. et al. Robust Monte-Carlo Simulations in Diffusion-MRI: Effect of the Substrate Complexity and Parameter Choice on the Reproducibility of Results. Front. Neuroinform. 14, 8 (2020).
16. van Gelderen, P., DesPres, D., van Zijl, P. C. & Moonen, C. T. Evaluation of restricted diffusion in cylinders. Phosphocreatine in rabbit leg muscle. J. Magn. Reson. B 103, 255–260 (1994).
17. Veraart, J. & Novikov, D. S. Axon radius mapping. (2019). https://github.com/NYU-DiffusionMRI/AxonRadiusMapping
18. Kroenke, C. D., Ackerman, J. J. H. & Yablonskiy, D. A. On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn. Reson. Med. 52, 1052–1059 (2004).
Figures