0644
What can a rat tell about physics beyond Standard Model: Exchange or structural disorder?1CIBM Center for Biomedical Imaging, Lausanne, Switzerland, 2Animal Imaging and Technology, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 3Dept. of Radiology, New York University School of Medicine, New York, NY, United States
Synopsis
One fundamental challenge in brain microstructure is to establish the biophysical origin of effects beyond the “Standard Model” (SM) picture of non-exchanging Gaussian compartments. The intra-compartmental structural disorder competes with inter-compartmental water exchange. Here we show that in rats, the exchange dominates, and offer the picture of diffusion time effectively filtering out the contribution of unmyelinated axons with stronger dispersion. At long times, only the myelinated (non-exchanging) axons contribute to the intra-axonal SM compartment, and the rest is attributed to extra-axonal space.
Introduction
The Standard Model (SM) of diffusion in two non-exchanging Gaussian compartments1,2 – and its numerous variants1,3–8 – has been widely used to characterize white matter (WM) and even gray matter (GM) (Fig. 1). However, the deviations from the key Gaussian compartment assumption may lead to the dependence of estimated SM parameters on diffusion time, due to either intra-compartment non-Gaussianity or inter-compartment exchange9–13. However, these aspects have not been studied explicitly in vivo. Practically, these effects can be amplified with strong diffusion weighting. Here we exploit multi-shell data up to $$$b=10\,\text{ms}/\mu\text{m}^2$$$ at four diffusion times t to examine the time-dependence and b-value dependence of the SM parameter estimates in the rat brain in vivo.Methods
All experiments were approved by the local Service for Veterinary Affairs. Four adult Wistar rats (3 males) were scanned on a 14T Bruker system using a home-built surface quadrature transceiver. Diffusion MRI data were acquired using a PGSE EPI sequence, sampling 7 or 8 shells ($$$b=1\,–10\,\text{ms}/\mu\text{m}^2$$$) and 3 – 4 diffusion times ($$$t=11\,–45\,\text{ms}$$$) in a non-sequential order to avoid bias of scanner or animal stability (see Fig. 2 for acquisition parameters of each dataset).Images were denoised and corrected for Rician bias, Gibbs ringing and motion14–16. Diffusion and kurtosis tensors were estimated for each diffusion time using shells $$$b\leq2.5\,\text{ms}/\mu\text{m}^2$$$ and a weighted linear least-squares algorithm17, from which typical tensor metrics were derived. For each diffusion time, the SM parameters were estimated using the rotational invariant (RotInv) framework1 (nonlinear least squares), and subsets of shells as follows: (i) $$$b_\text{max}\leq2.5\,ms/\mu\text{m}^2$$$, (ii) $$$b_\text{max}\leq6\,ms/\mu\text{m}^2$$$, (iii) $$$b_\text{max}\leq10\,ms/\mu\text{m}^2$$$. The solution $$$D_{\text{a}}>D_{\text{e,}\parallel}$$$ was favored18–20 choosing the algorithm initialization accordingly.
Three WM bundles (internal capsule – IC, corpus callosum – CC and cingulum – CG) as well as a bilateral cortical ROI were segmented. Average metrics above (diffusion/kurtosis tensors, and SM parameters) were calculated for each ROI.
Results
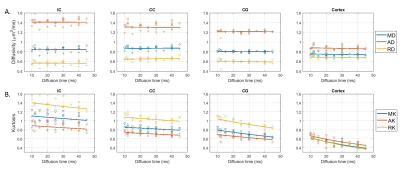
Over the range $$$t=11\,–45\,\text{ms}$$$ explored here, diffusivities displayed little to no time-dependence in all ROIs, while kurtosis decayed significantly (Fig. 3), particularly in the cortex, consistent with previous literature11,21,22.For the SM (Fig. 4), geometric parameters $$$f$$$ and $$$c_2=\langle\cos^2\theta\rangle$$$, where $$$\theta$$$ is the dispersion angle, showed significant time-dependence (and no dependence on $$$b_\text{max}$$$), while compartment diffusivities displayed a non-monotonic behavior as a function of $$$b_\text{max}$$$, with a switch between $$$b_\text{max}=\,2.5$$$ and $$$b_\text{max}\geq6$$$, but no systematic trend with diffusion time.
Discussion
DKI(t): With little time-dependence in overall diffusivity, the decreasing kurtosis as a function of diffusion time can be largely attributed to inter-compartment water exchange rather than to the effect of intra-compartmental structural disorder at these diffusion times12,21,22, especially as the faster decay constants are found for cortex, which contains the least myelinated fibers, and for cingulum, which may suffer from partial volume effects with surrounding GM. This is somewhat in contrast to human GM, where both observed K(t) and subtle D(t) suggested contributions of both structural disorder and exchange11.SM analysis: At least in WM ROIs, the intra-compartmental structural disorder is less relevant at our $$$t$$$ (due to relatively weak time-dependence of compartment diffusivities, compatible with the Gaussian compartments assumption of SM). The pronounced geometric features’ dependence on $$$t$$$, together with $$$K(t)$$$ above, suggests that the diffusion time plays the role of a filter that retains only the more myelinated – and possibly more aligned – axons as part of the intra-axonal space. Thus $$$f$$$ decreases while $$$c_2$$$ increases with $$$t$$$.
For ROIs with notable GM admixture (CG and cortex), the non-monotonic pattern with $$$b$$$ for $$$D_{\text{a}}$$$, which is time-independent for $$$b_\text{max}=\,2.5$$$ but decreases significantly with time for $$$b_\text{max}\geq\,6$$$, suggests the intra-neurite compartment cannot be assumed Gaussian at high b-values. The pattern is less clear for the extra-axonal diffusivities, as there are likely competing mechanisms that may balance each other out. For example, $$$D_e^\parallel$$$ may increase with $$$t$$$ as a result of exchange with the intra-axonal space $$$D_{\text{a}}>D_{\text{e,}\parallel}$$$, and decrease with $$$t$$$ as a result of either non-Gaussian contributions or a more hindered medium – axially – with disperse neurites increasingly assigned to the extra-axonal space. Similarly, $$$D_e^\perp$$$ may decrease with $$$t$$$ as a result of exchange with the intra-axonal space ($$$D_{\text{e,}\perp}>D_{\text{a,}\perp}\equiv0$$$) or due to non-Gaussian contributions, and increase as a result of disperse neurites – possibly orthogonal to main orientation – being assigned to the extra-axonal space.
SM applicability rests on compartment Gaussianity. Structural disorder causes intra-compartment non-Gaussian effects: the decrease of compartmental diffusivity with $$$t$$$, and non-zero $$$K_c(t)$$$ for each compartment $$$c=a,e$$$ beyond the SM. As a result, the model would adjust to absorb $$$K_c(t)$$$ into $$$D_c(t)$$$, resulting in an underestimation of $$$D_c$$$ most pronounced at short $$$t$$$ (when $$$K_c$$$ is largest). This effect would compete with genuine $$$D_c(t)$$$ decrease.
Conclusions
One fundamental challenge in brain microstructure is to establish the biophysical origin of effects beyond the SM picture of non-exchanging Gaussian compartments. The intra-compartmental structural disorder competes with inter-compartmental water exchange. Here we showed that in rats, the exchange dominates, and offer the picture of diffusion time effectively filtering out the contribution of unmyelinated axons with stronger dispersion. At long times, this picture suggests that only the myelinated (non-exchanging) axons contribute to the intra-axonal SM compartment, and the rest is asymptotically attributed to extra-axonal space.Acknowledgements
The authors acknowledge access to the facilities and expertise of the CIBM Center for Biomedical Imaging, a Swiss research center of excellence founded and supported by Lausanne University Hospital (CHUV), University of Lausanne (UNIL), Ecole polytechnique fédérale de Lausanne (EPFL), University of Geneva (UNIGE) and Geneva University Hospitals (HUG). D.S.N is supported by NIH under NINDS award R01 NS088040 and by the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center: P41 EB017183.References
1. Novikov, D. S., Veraart, J., Jelescu, I. O. & Fieremans, E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage 174, 518–538 (2018).
2. Novikov, D. S., Fieremans, E., Jespersen, S. N. & Kiselev, V. G. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR Biomed. 32, e3998 (2019).
3. Zhang, H., Schneider, T., Wheeler-Kingshott, C. A. & Alexander, D. C. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61, 1000–16 (2012).
4. Fieremans, E., Jensen, J. H. & Helpern, J. A. White matter characterization with diffusional kurtosis imaging. Neuroimage 58, 177–88 (2011).
5. McKinnon, E. T., Helpern, J. A. & Jensen, J. H. Modeling white matter microstructure with fiber ball imaging. NeuroImage 176, 11–21 (January 8).
6. Kaden, E., Kelm, N. D., Carson, R. P., Does, M. D. & Alexander, D. C. Multi-compartment microscopic diffusion imaging. NeuroImage 139, 346–359 (2016).
7. Jespersen, S. N. et al. Neurite density from magnetic resonance diffusion measurements at ultrahigh field: comparison with light microscopy and electron microscopy. Neuroimage 49, 205–16 (2010).
8. Jelescu, I. O., Palombo, M., Bagnato, F. & Schilling, K. G. Challenges for biophysical modeling of microstructure. J. Neurosci. Methods 344, 108861 (2020).
9. Veraart, J. et al. Noninvasive quantification of axon radii using diffusion MRI. eLife 9, e49855 (2020).
10. Fieremans, E. et al. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. NeuroImage 129, 414–427 (2016).
11. Lee, H.-H., Papaioannou, A., Novikov, D. S. & Fieremans, E. In vivo observation and biophysical interpretation of time-dependent diffusion in human cortical gray matter. NeuroImage 222, 117054 (2020).
12. Jelescu, I. O. & Novikov, D. S. Water exchange time between gray matter compartments in vivo. in Proc. Intl. Soc. Mag. Reson. Med. 28 (2020).
13. Jespersen, S. N., Olesen, J. L., Hansen, B. & Shemesh, N. Diffusion time dependence of microstructural parameters in fixed spinal cord. Neuroimage 182, 329–342 (2018).
14. Veraart, J. et al. Denoising of diffusion MRI using random matrix theory. Neuroimage 142, 394–406 (2016).
15. Kellner, E., Dhital, B., Kiselev, V. G. & Reisert, M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn. Reson. Med. 76, 1574–1581 (2016).
16. Jenkinson, M., Bannister, P., Brady, M. & Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 17, 825–41 (2002).
17. Veraart, J., Sijbers, J., Sunaert, S., Leemans, A. & Jeurissen, B. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. Neuroimage 81, 335–46 (2013).
18. Kunz, N., da Silva, A. R. & Jelescu, I. O. Intra- and extra-axonal axial diffusivities in the white matter: Which one is faster? Neuroimage 181, 314–322 (2018).
19. Dhital, B., Reisert, M., Kellner, E. & Kiselev, V. G. Intra-axonal diffusivity in brain white matter. Neuroimage 189, 543–550 (2019).
20. Howard, A. F. et al. Estimating intra-axonal axial diffusivity in the presence of fibre orientation dispersion. bioRxiv 2020.10.09.332700 (2020) doi:10.1101/2020.10.09.332700.
21. Aggarwal, M., Smith, M. D. & Calabresi, P. A. Diffusion-time dependence of diffusional kurtosis in the mouse brain. Magn. Reson. Med. 84, 1564–1578 (2020).
22. Pyatigorskaya, N., Le Bihan, D., Reynaud, O. & Ciobanu, L. Relationship between the diffusion time and the diffusion MRI signal observed at 17.2 Tesla in the healthy rat brain cortex. Magn Reson Med 72, 492–500 (2014).
Figures