0641
Diffusion MRI-Based Cytoarchitecture Measurements in Brain Gray Matter using Likelihood-Free Inference1Université Paris-Saclay, Inria, CEA, Palaiseau, France
Synopsis
We propose a new method to solve the inverse problem of relating the diffusion MRI signal with cytoarchitectural characteristics in brain gray matter. Specifically, our method has quantitative sensitivity to soma density and volume. Our solution is twofold. First, we propose a new forward model that relates summary statistics of the dMRI signal with tissue parameters, relying on six b-shells only. We then apply a likelihood-free inference based algorithm to invert the proposed model, which not only estimates the tissue parameters that best describe the acquired diffusion signal, but also a full posterior distribution over the parameter space.
Introduction
Effective characterisation of the brain grey matter cytoarchitecture with quantitative sensitivity to soma density and volume remains an unsolved challenge in diffusion MRI (dMRI). Current methods require demanding acquisitions and stabilise parameter fitting by enforcing constraints. Yet, these still encounter large indetermination areas in the solution space making the results unstable1. We propose a new forward model requiring only six relatively sparse b-shells and that avoids indeterminacies.Methods
Modeling Brain Gray Matter with a 3-compartment Model. We model grey matter tissue as three-compartmental2, moving away from the Standard Model designed for white matter. The acquired signal is considered as resulting from a convex mixture of signals arising from somas, neurites, and extra-cellular space (ECS), under a no-exchanges assumption2. Our direction-averaged grey matter signal model is then:$$\frac{\bar{S}(q)}{S(0)}={f_{n}}\bar{S}_{\mathrm{neurites}}({q}, {D_a})+{f_{s}}\bar{S}_{\mathrm{somas}}({q},{D_{s}},{r_{s}})+{f_{\mathrm{ECS}}}\bar{S}_{\mathrm{ECS}}({q},D_{e}), \mathrm{with} ~q(b)=\frac{1}{2\pi}\sqrt{\frac{b}{\tau}}$$
fn, fs and fECS represent neurites, somas and ECS signal fractions respectively ($$$f_n+f_s+f_{\mathrm{ECS}}=1$$$); Da axial diffusivity inside neurites; Ds and De somas and extra-cellular diffusivities; and rs the average soma radius.
Neurites are modeled as 0-radius impermeable cylinders3:
$$\bar{S}_{\mathrm{neurites}}(q)\simeq\frac{1}{4\sqrt{\pi\tau{D_{a}}}}\cdot{q}^{-1}$$
Somas are modeled as spheres and follow the GPD approximation4:
$$-\log\bar{S}_{\mathrm{somas}}(q)=C({r_{s}},{D_{s}})\cdot{q}^2=q^2\frac{2}{{D_s}\delta^2}\sum_{m=1}^{\infty}\frac{\alpha_m^{-4}}{\alpha_m^{2}{r_s}^2-2}\cdot\left(2\delta-\frac{2+e^{-\alpha_m^2{D_s}(\Delta-\delta)}-e^{-\alpha_m^2{D_s}\delta}-e^{-\alpha_m^2{D_s}\Delta}+e^{-\alpha_m^2{D_s}(\Delta+\delta)}}{\alpha_m^2{D_s}}\right)$$
We exploit this relation to extract a parameter $$$C_s=C(r_{s},D_{s})[m^{2}]$$$ which, at fixed diffusivity Ds is modulated by the soma radius.The ECS is approximated as isotropic Gaussian diffusion:
$$-\log(\bar{S}_{\mathrm{ECS}}(q))=(2\pi{q})^2\tau{D_{e}}$$
An Invertible 3-compartment Model: dMRI Summary Statistics. Solving the inverse problem directly from Eq.1 leads to indeterminacies and bad parameter estimations. We therefore introduce rotationally invariant summary statistics to relate the dMRI signal to tissue parameters.
First, we compute a q-bounded RTOP, a direct measure of the restrictions of the diffusing fluid molecule motion5:
$$\mathrm{RTOP}(q)=4\pi\int_{0}^{q}{\frac{\bar{S}(\eta)}{S(0)}}\eta^2d\eta$$
For q large enough, $$$\mathrm{RTOP}(q)$$$ on our 3-compartment model (Eq.1) becomes:
$$\mathrm{RTOP}(q)=\underbrace{{f_s}\left(\frac{\pi}{{C_s}}\right)^{3/2}+\frac{{f_{\mathrm{ECS}}}}{8(\pi\tau{D_{e}})^{3/2}}}_{a_\mathrm{fit}}+\underbrace{\frac{{f_{n}}}{2}\cdot\sqrt{\frac{\pi}{\tau{D_a}}}}_{b_\mathrm{fit}}\cdot q^2$$
Three different q-values are needed to estimate $$$a_{\mathrm{fit}}$$$ and $$$b_{\mathrm{fit}}$$$.
Secondly, we extended LEMONADE1, based on a moment decomposition for small q-values, to our 3-compartment model and extract four rotational invariant scalar indices that quantify grey matter microstructure:
$$\begin{cases}M^{(2),0}={f_n}{D_a}+3{f_s}\frac{{C_s}}{(2 \pi)^2\tau}+3{f_{\mathrm{ECS}}}D_e\\M^{(2),2}={f_n}{D_a}{p_2}\\M^{(4),0}={f_n}{D_a}^2+5{f_s}\left(\frac{{C_s}}{(2 \pi)^2\tau}\right)^2+5{f_{\mathrm{ECS}}}D_e^2\\M^{(4),2}={f_n}{D_a}^2{p_2}\end{cases}$$
where p2 is a scalar measure of neurite orientation dispersion1. A minimum of three q-values with b(q)≈3ms/μm2 are required.
We assume De nearly-constant per subject acquisition and estimate it as the mean diffusivity in the subject's ventricles6. Combining equations 6 and 7 and adding the $$$f_n+f_s+f_{\mathrm{ECS}}=1$$$ constraint, we obtain a system of 7 equations and 6 unknowns.
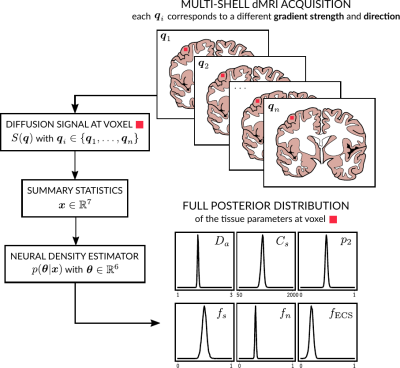
Solving the inverse problem via likelihood free inference. We invert our model using a Bayesian approach based on likelihood-free inference (LFI)7. Our algorithm produces an approximation of the full posterior distribution p(θ|x0) over the parameter space for a given observation x0. This can be used to determine which parameter vector θ=(Da, Cs, p2, fs, fn, fECS) is the most likely to have produced x0 and the corresponding confidence intervals. Moreover, it describes in which regions of the parameter space the model presents indeterminacies. Our LFI procedure follows the setup from 8 and approximates the posterior distribution using normalizing flows (a special class of deep neural networks) trained over a set of repeated simulations from the forward model.
Results and Discussion
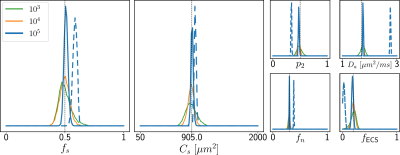
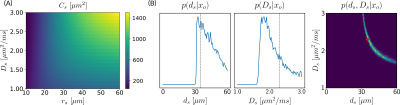
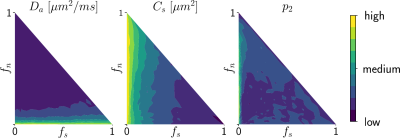
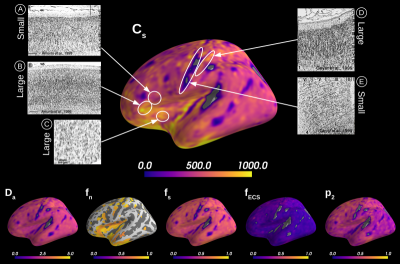
Simulations. We validated the proposed method using LFI on neuron simulations from neuromorpho.org using dmipy9. We present on Fig.2 results for θ=(1.7, 905, 0.5, 0.5, 0.3, 0.2), which corresponds to spheres with a 35μm diameter and 2.3μm2/ms diffusivity. Two acquisition setups have been considered, both with $$$\delta/\Delta=12.9/21.8ms$$$ and 128 b-shells with uniformly distributed directions. Setup $$$\mathcal{A}$$$ corresponds to an "ideal" case with 10 b-values between 0 and 10ms/μm2. Setup $$$\mathcal{B}$$$ reproduces the more challenging setup from the HCP MGH dataset10, with only 5 b-values: 0, 1, 3, 5, and 10ms/μm2. We interpolated an extra point at 0.1ms/μm2 using MAPL11 to improve moment estimation on the Spiked LEMONADE step. On Fig.3, we estimate the soma radius and diffusivity separately. LFI is unable to determine among all possible solutions which one is the ground truth, but using the parameter $$$C_s$$$ instead of $$$r_s$$$ and $$$D_s$$$ enables to avoid model indeterminacy. A low standard deviation is also observed for signals generated in grey matter tissue conditions, where a soma predominance is expected (Fig.4).Experiments. We applied the proposed method to the HCP MGH Adult Diffusion dataset10, whose acquisition is similar to setup $$$\mathcal{B}$$$. $$$D_e$$$ was estimated as the mean diffusivity in the ventricles. Fig.5 presents the mean estimations across subjects, where overlay colormaps are masked showing only areas where parameters are stable, i.e. when their value was larger than 2 times the LFI-obtained standard deviation of the fitted posterior. Our figure assesses qualitatively the results on soma size by comparing with nissl-stained histological studies12,13,14. This qualitative comparison shows good agreement between different cortical areas and our parameter $$$C_s$$$ which, under nearly-constant intra-soma diffusion $$$D_s$$$, is modulated by soma size.
Conclusion
We presented a methodology based on Bayesian inference with modern tools from neural networks to estimate the tissue parameters and their full posterior distribution out of grey matter dMRI signals. This rich description provides many useful tools, such as assessing the quality of the parameter estimation or characterizing regions in the parameter space where it is harder to invert the model. Moreover, our proposal alleviates limitations from current methods by not requiring physiologically unrealistic constraints on the parameters and avoiding indeterminacies when estimating them.Acknowledgements
We thank Dmitry Novikov for stimulating conversations and his implementation of LEMONADE.
This work was supported by the ERC-StG NeuroLang grant number 757672 and the ANR/NSF NeuroRef grants.
References
1. Novikov, D.S., Veraart, J., Jelescu, I.O., Fieremans, E.: Rotationally-invariant map-ping of scalar and orientational metrics of neuronal microstructure with diffusion MRI.NeuroImage174, 518–538 (Jul 2018)
2. Palombo, M., Ianus, A., Guerreri, M., Nunes, D., Alexander, D.C., Shemesh, N., Zhang,H.: SANDI: A compartment-based model for non-invasive apparent soma and neuriteimaging by diffusion MRI. NeuroImage215, 116835 (2020)
3. Veraart, J., Nunes, D., Rudrapatna, U., Fieremans, E., Jones, D.K., Novikov, D.S.,Shemesh, N.: Noninvasive quantification of axon radii using diffusion MRI. eLife9(Feb 2020)
4. Balinov, B., Jönsson, Linse, P., Söderman, O.: The NMR Self-Diffusion Method Ap-plied to Restricted Diffusion. Simulation of Echo Attenuation form Molecules in Spheresand between Planes (1993)
5. Mitra, P.P., Latour, L.L., Kleinberg, R.L., Sotak, C.H.: Pulsed-field-gradient NMRmeasurements of restricted diffusion and the return-to-origin probability. Journal ofMagnetic Resonance114, 47–58 (1995)
6. Menon, V., Gallardo, G., Pinsk, M.A., Nguyen, V.D., Li, J.R., Cai, W., Wassermann,D.: Microstructural organization of human insula is linked to its macrofunctional cir-cuitry and predicts cognitive control. elife9, e53470 (2020)
7. Cranmer, K., Brehmer, J., Louppe, G.: The frontier of simulation-based inference.Proceedings of the National Academy of Sciences117(48), 30055–30062 (2020)
8. Greenberg, D., Nonnenmacher, M., Macke, J.: Automatic posterior transformationfor likelihood-free inference. In: Proceedings of the 36th International Conference onMachine Learning, vol. 97, pp. 2404–2414, PMLR (2019)
9. Fick, R.H.J., Wassermann, D., Deriche, R.: The Dmipy Toolbox: Diffusion MRI Multi-Compartment Modeling and Microstructure Recovery Made Easy. Frontiers in Neuroin-formatics13(Oct 2019)
10. Setsompop, K., Kimmlingen, R., Eberlein, E., Witzel, T., Cohen-Adad, J., McNab, J.,Keil, B., Tisdall, M., Hoecht, P., Dietz, P., Cauley, S., Tountcheva, V., Matschl, V.,Lenz, V., Heberlein, K., Potthast, A., Thein, H., Horn, J.V., Toga, A., Schmitt, F.,Lehne, D., Rosen, B., Wedeen, V., Wald, L.: Pushing the limits of in vivo diffusionMRI for the Human Connectome Project. NeuroImage80, 220 – 233 (2013)
11. Fick, R.H., Wassermann, D., Caruyer, E., Deriche, R.: MAPL: Tissue microstructureestimation using Laplacian-regularized MAP-MRI and its application to HCP data.NeuroImage134, 365–385 (Jul 2016)
12. Allman, J.M., Tetreault, N.A., Hakeem, A.Y., Manaye, K.F., Semendeferi, K., Erwin,J.M., Park, S., Goubert, V., Hof, P.R.: The von Economo neurons in frontoinsular andanterior cingulate cortex in great apes and humans. Brain Structure and Function214,495–517 (Jun 2010)
13. Amunts, K., Schleicher, A., Bürgel, U., Mohlberg, H., Uylings, H.B., Zilles, K.: Broca’sregion revisited: Cytoarchitecture and intersubject variability. Journal of ComparativeNeurology412(2), 319–341 (1999)
14. Geyer, S., Schleicher, A., Zilles, K.: Areas 3a, 3b, and 1 of Human Primary Somatosen-sory Cortex. NeuroImage10(1), 63–83 (Jul 1999), ISSN 10538119
Figures