0640
Parameter estimation for the GRAMMI (GRAy Matter Microstructure Imaging) model of two exchanging compartments in the rat cortex in vivo1Dept. of Physics, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2Centre for Medical Image Computing and Dept. of Computer Science, University College London, London, United Kingdom, 3Center for Biomedical Imaging, Dept. of Radiology, New York University, New York, NY, United States, 4CIBM Center for Biomedical Imaging, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
Synopsis
Developing a relevant model for brain gray matter is a complex task. As opposed to white matter, features such as inter-compartment water exchange or soma should likely be modeled. In this work we examine the performance of a variant of the Kärger Model, called GRAMMI, that accounts for exchange, both on synthetic and experimental data. We show q-t coverage is necessary for reliable model parameter estimation at the individual voxel level and compare two regression approaches. Future work includes protocol optimization and the extension of the GRAMMI model to account for soma.
Introduction
The Standard Model (SM)1 of diffusion in white matter (WM) relies on modeling axons as impermeable sticks. This assumption has been shown to break in gray matter2–5 (GM). Potential contributors to this deviation are non-negligible exchange between compartments over the typical diffusion times of MRI experiments ($$$10–100$$$ ms)2,3,5,6, an additional soma compartment7,8 and, for long gradient pulse durations only, neurite size and curvature8,9.An extension of the Kärger model of two exchanging compartments to anisotropic media has been recently proposed2,3,10,11 but the feasibility of estimating the full model – characterized by four parameters – without additional constraints has not been evaluated.
Here we provide a comprehensive characterization of the accuracy and precision of parameter estimates both in simulations and on data acquired in the rat cortex in vivo for different acquisition protocols. We further investigate the impact of the regression method on parameter estimation by comparing non-linear least squares (NLLS) and deep learning (DL).
Methods
The GRAMMI model (GRAy Matter Microstructure Imaging) consists in the isotropic average $$$\bar{S}$$$ of the Kärger model signal $$$\mathcal{K}$$$ for two anisotropic compartments (intra- and extra-neurite spaces), where we further assume that $$$D_{e,\bot}=D_{e,\parallel}\equiv D_e$$$ in the extracellular space, given low macroscopic anisotropy of GM. The estimated parameters are the intra-neurite fraction $$$f$$$, the inter-compartment exchange time $$$t_{ex}$$$, the intra-neurite diffusivity $$$D_{i,\parallel}$$$ and the extracellular diffusivity $$$D_e$$$.\begin{align}
(1)\hspace{1cm}&\bar{S}(q,t_d)=S(0)\int_0^1 \mathcal{K}(q,\mathbf{g},t_d;\mathbf{p},\mathbf{n})
d (\mathbf{g}\cdot\mathbf{n}) \\
(2)\hspace{1cm}&\mathcal{K}(q,\mathbf{g},t_d;\mathbf{p},\mathbf{n})=f^{'}e^{-q^2t_dD_i^{'}}+(1-f^{'})e^{-q^2t_dD_e^{'}} \\
(3)\hspace{1cm}&D^{'}_{i,e}=\frac{1}{2}\bigg(D_{i,\parallel}(\mathbf{g}\cdot\mathbf{n} )^2+D_e+\frac{1}{q^2 t_{ex}} \mp\big[[D_e-D_{i,\parallel}(\mathbf{g}\cdot\mathbf{n} )^2+\frac{2f-1}{t_{ex}}]^2+\frac{4f(1-f)}{q^4t^2_{ex}}\big ]^{\frac{1}{2}}\bigg) \\
(4)\hspace{1cm}&f^{'}=\frac{1}{D_i^{'}-D_e^{'}}(fD_{i,\parallel}(\mathbf{g}\cdot\mathbf{n} )^2+(1-f)D_e-D_e^{'})
\end{align}
Simulations. Synthetic signals ($$$N=10^4$$$) were generated based on Eqs. 1 – 4 using a protocol with $$$b=[0, 1:1.5:10]$$$ ms/μm2 and diffusion times $$$t_d=[12,20,30,40]$$$ ms, both noiseless and with Rician noise ($$$SNR=100$$$). The ground truth (GT) was either fixed to $$$[t_{ex},D_{i,\parallel},D_e,f]=[20,2.5,0.75,0.34]$$$ with only the noise realization (and the NLLS fit initialization) changing for each iteration, or randomly chosen within physical ranges, that is $$$t_{ex}\in[5,120]$$$, $$$D_{i,\parallel}\in[1.5,3]$$$, $$$D_e\in[0,1.5]$$$ and $$$f\in[0.1,0.9]$$$, thus enforcing the physically relevant solution of the GRAMMI model12 ($$$D_{i,\parallel}>D_e$$$).
Model fitting. Estimations where done either by fitting the signals for each diffusion time separately (as in standard multi-shell datasets) or jointly. NLLS used trust-region-reflective algorithm with box constraints for multi-shell data and quasi-Newton algorithm without constraints for multi-shell multi-$$$t_d$$$ data. Deep regression was done using 3 hidden layers MLPs with 16*(#b)*(#td) units each, with leaky-relu activations as non-linearities. Parameters to be estimated were scaled in the (-1, 1) range and signals were log-transformed before being used as network inputs. Training was done using $$$10^5$$$ signals and their corresponding parameters, both for noiseless and noisy estimations. In the second case we set $$$SNR\in[80,120]$$$, to train the network for multiple noise levels as is the case in experimental datasets.
Experimental. All experiments were approved by the local Service for Veterinary Affairs. Four adult Wistar rats were scanned on a 14T Bruker system using a home-built surface quadrature transceiver. Diffusion MRI data were acquired using a PGSE EPI sequence (see Fig. 1 for all acquisition parameters).
Images were denoised and corrected for Rician bias, Gibbs ringing and motion13-15. Powder-average signal was computed for each shell. A bilateral cortical ROI was manually drawn. For multi-shell multi-$$$t_d$$$ data, parametric maps of GRAMMI estimates were computed.
Results
In a realistic case of high – but finite – SNR, multi-shell diffusion data at a single diffusion time are insufficient to estimate $$$t_{ex}$$$ and $$$D_{i,\parallel}$$$ from GRAMMI, only $$$f$$$ and $$$D_e$$$ can be characterized (Fig. 2).Pooling multi-shell multi-$$$t_d$$$ data together restores sensitivity to the estimation of both $$$t_{ex}$$$ and $$$D_{i,\parallel}$$$ (Fig. 3). Experimental data are consistent with simulations and show good agreement between NLLS and DL approaches, as well as feasibility of GRAMMI parametric maps (Fig. 4).
Discussion and conclusions
Inter-compartment exchange likely plays an important role in GM diffusion and should be accounted for in biophysical models of GM when $$$t_d>25–70$$$ ms. GRAMMI is a promising candidate for this role but, on typical multi-shell single diffusion time data, its four parameters cannot be estimated all at once, with only $$$f$$$ and $$$D_e$$$ showing acceptable performance. We note however that accounting for exchange readily stabilizes the intra-neurite fraction $$$f$$$ with respect to diffusion time, as opposed to models with no exchange where the apparent $$$f$$$ decreases with increasing $$$t_d$$$. Exploiting multi-shell multi-$$$t_d$$$ data together dramatically improves the estimation of $$$t_{ex}$$$, and, to a more limited extent, of $$$D_{i,\parallel}$$$. Thus, the GRAMMI model can be estimated without additional assumptions or fixed parameters. Of note that the range of diffusion times should be tuned to the expected range for $$$t_{ex}$$$ as estimates of $$$t_{ex} > 2t_{d,max}$$$ are unreliable.One limitation of the multi-shell multi-$$$t_d$$$ approach is the underlying assumption that compartment diffusivities are time-independent in the respective $$$q$$$-$$$t$$$ range. But evidence of small diffusion time-dependence in rat and human cortex for PGSE diffusion time ranges support for now this simplifying assumption3,4,16,17. GRAMMI also neglects the soma compartment, which may confound results7,8. Further investigation is needed to clarify the relative contributions of exchange or soma to the signal features. Future work will focus on determining a minimal acquisition protocol in $$$q$$$-$$$t$$$ space for GRAMMI, including $$$b_{max}$$$, number of shells and of diffusion times, on its clinical implementation and potential extension to include a soma compartment with exchange.
Acknowledgements
This work was made possible thanks to the CIBM Center for Biomedical Imaging, founded and supported by Lausanne University Hospital (CHUV), University of Lausanne (UNIL), Ecole Polytechnique Federale de Lausanne (EPFL), University of Geneva (UNIGE) and Geneva University Hospitals (HUG).
MP is supported by the UKRI Future Leaders Fellowship MR/T020296/1.
D.S.N. is supported by NIH under NINDS award R01 NS088040 and by the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center: P41 EB017183
References
1. Novikov, D. S., Veraart, J., Jelescu, I. O. & Fieremans, E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage 174, 518–538 (2018).
2. Veraart, J., Fieremans, E., Rudrapatna, U., Jones, D. K. & Novikov, D. S. Biophysical modeling of the gray matter: does the ‘stick’ model hold? in Proc. Intl. Soc. Mag. Reson. Med. 26 1094 (2018).
3. Jelescu, I. O. & Novikov, D. S. Water exchange time between gray matter compartments in vivo. in Proc. Intl. Soc. Mag. Reson. Med. 28 (2020).
4. Lee, H.-H., Papaioannou, A., Novikov, D. S. & Fieremans, E. In vivo observation and biophysical interpretation of time-dependent diffusion in human cortical gray matter. NeuroImage 222, 117054 (2020).
5. Veraart, J. et al. Nonivasive quantification of axon radii using diffusion MRI. eLife 9, e49855 (2020).
6. Williamson, N. H. et al. Magnetic resonance measurements of cellular and sub-cellular membrane structures in live and fixed neural tissue. Elife 8, (2019).
7. Palombo, M. et al. SANDI: A compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. NeuroImage 215, 116835 (2020).
8. Olesen, J. L. & Jespersen, S. N. Stick power law scaling in neurons withstands realistic curvature and branching. in Proc. Intl. Soc. Mag. Reson. Med. 28 716.
9. Özarslan, E., Yolcu, C., Herberthson, M., Knutsson, H. & Westin, C.-F. Influence of the Size and Curvedness of Neural Projections on the Orientationally Averaged Diffusion MR Signal. Front. Phys. 6, (2018).
10. Kärger, J. NMR self-diffusion studies in heterogeneous systems. Advances in Colloid and Interface Science 23, 129–148 (1985).
11. Fieremans, E., Novikov, D. S., Jensen, J. H. & Helpern, J. A. Monte Carlo study of a two-compartment exchange model of diffusion. NMR in biomedicine 23, 711–24 (2010).
12. Kunz, N., da Silva, A. R. & Jelescu, I. O. Intra- and extra-axonal axial diffusivities in the white matter: Which one is faster? NeuroImage 181, 314–322 (2018).
13. Veraart, J. et al. Denoising of diffusion MRI using random matrix theory. NeuroImage 142, 394–406 (2016).
14. Kellner, E., Dhital, B., Kiselev, V. G. & Reisert, M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magnetic Resonance in Medicine 76, 1574–1581 (2016).
15. Jenkinson, M., Bannister, P., Brady, M. & Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage 17, 825–41 (2002).
16. Pyatigorskaya, N., Le Bihan, D., Reynaud, O. & Ciobanu, L. Relationship between the diffusion time and the diffusion MRI signal observed at 17.2 Tesla in the healthy rat brain cortex. Magnetic resonance in medicine 72, 492–500 (2014).
17. Aggarwal, M., Martin, K., Smith, M. & Calabresi, P. Diffusion-time dependence of diffusional kurtosis in the mouse brain using pulsed and oscillating gradients. in Proc. Intl. Soc. Mag. Reson. Med. 26 1093 (2018).
Figures

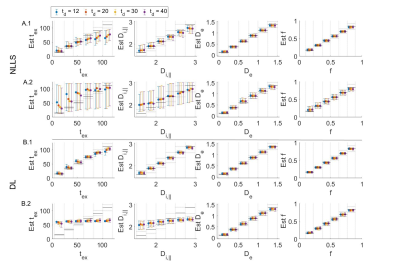
Fig.2: Simulation results fitting multi-shell data for each diffusion time separately using NLLS (A) or DL (B). Displayed is the GT vs estimation for 104 set of random parameters. Markers correspond to the median & IQR in the corresponding bin. Black lines are the ideal estimation ±10% error. In the noiseless case, for NLLS (A1) there is already a loss of precision on Di and the tex estimate plateaus beyond 70 ms due to short diffusion times. For DL (B1) the accuracy and precision are good on all parameters. As noise is added (A2-B2, SNR = 100) the sensitivity to tex and Di is lost.
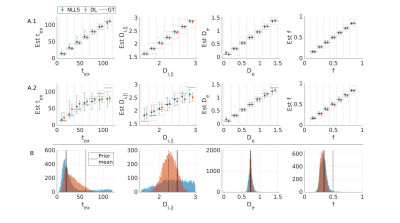
Fig.3: Simulation results fitting multi-shell multi-td data jointly for random (A) and fixed (B) GT. A: Displayed are the medians & IQR in each bin. Black lines: ideal estimation ±10 % error. Without noise (A1) DL and NLLS fit all parameters with high accuracy and precision. At SNR=100 (A2) some sensitivity to Di and high tex values is lost but still better than single td fits (Fig.2). DL has better precision than NLLS. B: At SNR=100, good accuracy is achived for tex, De and f with both NLLS and DL. For Di the precision is poor with NLLS while DL biases the outcome
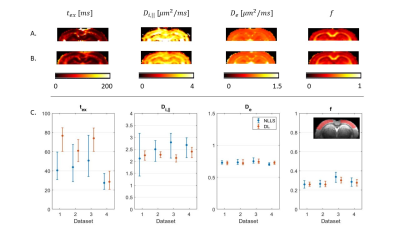
Fig.4: GRAMMI parametric maps calculated with NLLS (A) & DL (B) from a multi-shell multi-td dataset. The maps are overall homogeneous, with good differentiation between GM & WM. C: Median & IQR of model parameters in the cortex ROI across the 4 datasets. Experimental trends agree with the simulations. For De and f, NLLS and DL results are consistent, with better precision for DL Regarding tex the two methods agree very well for Dataset #4, which had the highest SNR (larger voxels), but the specific tex estimate may be biased due to only 3 diffusion times available instead of 4 (Fig. 1).