0639

Localization regime of diffusion in human gray matter on a high-gradient MR system: Sensitivity to soma size

Hong-Hsi Lee¹, Els Fieremans¹, Susie Y Huang², Qiyuan Tian², and Dmitry S Novikov¹
¹New York University School of Medicine, New York, NY, United States, ²Department of Radiology, A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States

Synopsis

In vivo estimation of cell dimension using diffusion MRI usually requires biophysical modeling of multiple compartments in biological tissues. However, the signal decomposition of multiple compartments is non-trivial due to limited amount of data and scan time. Instead, by applying strong diffusion gradients, a universal localization regime emerges: Magnetization far away from the cell boundaries vanishes, and only that near the boundaries within a thickness of localization length contributes to signal. Here, using Connectome gradients, we for the first time achieve the localization regime in vivo, and estimate the soma size in cortical brain gray matter of two healthy subjects.

Introduction

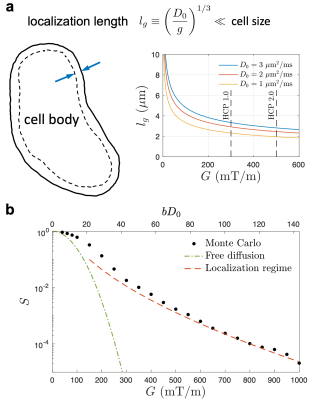
Diffusion MRI (dMRI) is sensitive to the cell dimension, such as axon diameter [1-4], cell body (e.g., soma) size [5] and cancer cell size [6]. To estimate tissue length scales, most biophysical modeling of dMRI incorporates contributions from multiple compartments (e.g., intra-/extra-cellular spaces) [1-6], whose signals are modeled by cumulant expansion [7]. However, it is difficult to decompose compartmental signals due to limited amount of data acquired in feasible scan time. Fortunately, at high diffusion gradients $$$G$$$ (Larmor gradient $$$g=\gamma{}G$$$), cumulant expansion loses its validity, and a universal compartment-independent "localization regime" emerges [8,9]: The strong gradient saturates all magnetization except that near the boundaries (e.g., cell membranes) within a thickness of localization length $$$l_g\propto{}g^{-1/3}$$$. This signal sensitivity to cell boundaries yields an estimate of cell size. Here, we for the first time achieve the localization regime in vivo, on a Connectome scanner using $$$G\lesssim300$$$ mT/m in two healthy subjects. This allows us to estimate the soma radius in brain cortex.

Theory

Conventionally, dMRI signal $$$S$$$ of low diffusion-weighting $$$b\propto{}g^2$$$ is approximated by $$$S\sim\exp(-bD)$$$, with apparent diffusivity $$$D$$$ lower than the intrinsic one $$$D_0$$$. However, in localization regime, dMRI signal measured by applying strong gradients deviates from the cumulant expansion and decays as $$$-\ln{}S\sim(bD_0)^{1/3}\propto{}g^{2/3}$$$. Due to strong gradients, magnetization far from the boundaries vanishes, and only that within a layer of $$$l_g\equiv(D_0/g)^{1/3}$$$ near the boundaries contribute to the measured signals (Figure 1a) [8]. The localization regime emerges when the localization length is much smaller than the characteristic length scales (e.g., cell size, curvature radius) and diffusion length $$$l_\delta=\sqrt{D_0\delta}$$$, where the gradient pulse width $$$\delta\sim{}t$$$ is comparable with the diffusion time $$$t$$$ of a pulsed-gradient sequence. For diffusion in a medium of spheres, the dMRI signal in localization regime is given by [8,9]
$$S_\pm(g,\delta)\simeq{}C_\pm\cdot\left(\frac{l_g}{r}\right)^{10/4}\cdot\exp\left(-a_1\frac{l_\delta^2}{l_g^2}-\frac{2l_\delta^2}{r^{1/2}l_g^{3/2}}\pm\frac{\sqrt{3}l_\delta^2}{a_1rl_g}\right)\,,\quad(1)$$
where $$$a_1=1.02$$$, and $$$S_\pm$$$ are signals inside and outside the spheres, with corresponding constants $$$C_\pm$$$ related to the diffusion eigenmodes. Empirically, $$$C_+\sim13$$$ is estimated based on numerical simulations (Figure 1b). For simplicity, we take $$$C_-\sim{}C_+$$$ just for estimating the scale of radius $$$r$$$. Finally, the overall normalized signal is
$$S\simeq{}\frac{S_++S_-}{2}\,.\quad(2)$$

Method

Monte Carlo Simulation
Numerical simulation of diffusion was performed within an impermeable sphere of radius $$$r$$$=10 μm. We applied 1.2×10⁸ random walkers diffusing over 2×10⁵ steps with a step size $$$\sqrt{6D_0\delta{}t}$$$=0.042 μm, a step duration $$$\delta{}t$$$=1×10^-4 ms and the intrinsic diffusivity $$$D_0$$$=3 μm²/ms. Diffusion signals of pulsed-gradient sequence of $$$t=\delta$$$=10ms were calculated.

In vivo MRI
Two healthy subjects (23-25 y/o, F) underwent imaging on a HCP Siemens Skyra 3T scanner (maximal $$$G$$$=300 mT/m, slew rate=200 T/m/s) with a home-built 32-channel head coil [10] after providing consents. dMRI measurements using monopolar pulsed-gradient spin-echo sequence were performed with 3 protocols:
1) $$$t/\delta$$$=27/16 ms, $$$b$$$=[1, 2, 3, 5, 7.5, 10, 15, 20, 25, 30] ms/μm²,
2) $$$t/\delta$$$=24/13 ms, $$$b$$$=[0.6, 1.2, 1.8, 3, 4.5, 6, 9, 12, 15, 18] ms/μm²,
3) $$$t/\delta$$$=22/11 ms, $$$b$$$=[0.4, 0.8, 1.2, 2, 3, 4, 6, 8, 10, 12] ms/μm².
In the above protocols, we applied gradients $$$G$$$=50-275 mT/m, corresponding to $$$l_g$$$=6.0-3.4 μm when $$$D_0$$$=3 μm²/ms. For each scan, we obtained 2b=0 images and 32 diffusion-weighted-images (DWIs) per b-shell. Resolution=(2 mm)³, FOV=216×216 mm², 58 slices, TE/TR=62/5200 ms, PF=6/8, GRAPPA=2, SMS=2.

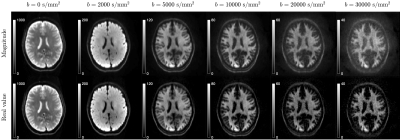
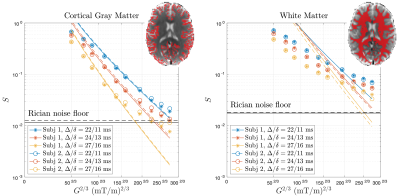
The shot-to-shot phase variation in each complex-valued DWI was eliminated [11], and the obtained real-valued DWIs were processed using DESIGNER pipeline [12]. For each pair of $$$t/\delta$$$, DWIs were averaged over directions for each b-shell. Then the signal model of localization regime in Eq. (2) was fitted to directionally averaged signals to estimate the soma radius in cortical gray matter (GM) region-of-interest (ROI). The $$$D_0$$$ was fixed at 3 μm²/ms during fitting. The data of $$$G$$$>100mT/m was included for fitting, and the noisy data hitting the noise floor [13] was excluded for fitting. The signal in white matter (WM) was also shown for reference.

Result

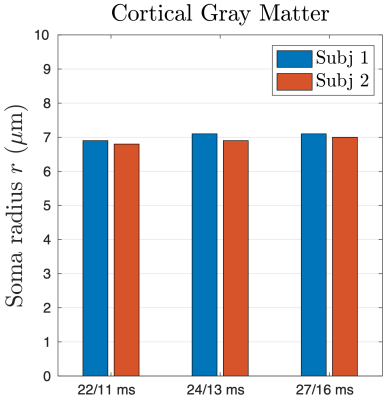
Numerical simulation is consistent with the functional form of $$$S_+$$$ in Eq. (1) in localization regime at strong gradients, yielding the constant value $$$C_+\simeq$$$13 (Figure 1b).

Elimination of shot-to-shot background phase variation reduces the Rician noise bias in directionally averaged signals (Figure 2). In cortical GM ROI, the signal is consistent with the fit of localization regime in Eq. (2) when $$$G\gtrsim$$$100mT/m until hitting the noise floor (Figure 3), and the estimated soma radius is $$$r$$$=7μm (Figure 4). In contrast, the signal in WM ROI can not be explained by localization regime (Figure 3).

Discussion and conclusion

We demonstrate the localization regime of dMRI signals at strong gradients via the numerical simulation and in vivo MRI in human cortical brain GM, where the estimated soma radius $$$r$$$~7 μm is consistent with the histology [14] and is larger than the $$$l_g$$$=3.4-6.0 μm in our experiments. In WM, however, dMRI signal is not compatible with the prediction of localization regime since the axon size~1 μm is smaller than the shortest localization length $$$l_g$$$~3.4 μm on the HCP scanner.

In conclusion, the dMRI measurement in localization regime enables to estimate soma size without modeling multiple compartments, and the need of DWIs at strong diffusion-weighting prompts developing ultra-high MR gradient systems and advanced denoising pipeline (e.g., ref. [15]) in future projects.

Acknowledgements

We would like to thank the BigPurple High Performance Computing Center of New York University Langone Health for numerical computations on the cluster. Research was supported by the National Institute of Neurological Disorders and Stroke of the NIH under awards R01 NS088040 and R21 NS081230, and by the National Institute of Biomedical Imaging and Bioengineering (NIBIB) of the NIH under award number U01 EB026996, and was performed at the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a Biomedical Technology Resource Center supported by NIBIB with the award P41 EB017183.

References

1. Veraart, J., Nunes, D., Rudrapatna, U., Fieremans, E., Jones, D. K., Novikov, D. S., & Shemesh, N. (2020). Noninvasive quantification of axon radii using diffusion MRI. Elife, 9, e49855.

2. De Santis, S., Jones, D. K., & Roebroeck, A. (2016). Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter. NeuroImage, 130, 91-103.

3. Alexander, D. C., Hubbard, P. L., Hall, M. G., Moore, E. A., Ptito, M., Parker, G. J., & Dyrby, T. B. (2010). Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage, 52(4), 1374-1389.

4. Assaf, Y., Blumenfeld‐Katzir, T., Yovel, Y., & Basser, P. J. (2008). AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 59(6), 1347-1354.

5. Palombo, M., Ianus, A., Guerreri, M., Nunes, D., Alexander, D. C., Shemesh, N., & Zhang, H. (2020). SANDI: a compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. NeuroImage, 116835.

6. Reynaud, O., Winters, K. V., Hoang, D. M., Wadghiri, Y. Z., Novikov, D. S., & Kim, S. G. (2016). Pulsed and oscillating gradient MRI for assessment of cell size and extracellular space (POMACE) in mouse gliomas. NMR in biomedicine, 29(10), 1350-1363.

7. Kiselev, V. G. (2010). The cumulant expansion: an overarching mathematical framework for understanding diffusion NMR. Diffusion MRI: theory, methods, and applications, 152-168.

8. Stoller, S. D., Happer, W., & Dyson, F. J. (1991). Transverse spin relaxation in inhomogeneous magnetic fields. Physical Review A, 44(11), 7459.

9. Moutal, N., Demberg, K., Grebenkov, D. S., & Kuder, T. A. (2019). Localization regime in diffusion NMR: theory and experiments. Journal of Magnetic Resonance, 305, 162-174.

10. Stockmann, J. P., Witzel, T., Keil, B., Polimeni, J. R., Mareyam, A., LaPierre, C., ... & Wald, L. L. (2016). A 32‐channel combined RF and B0 shim array for 3T brain imaging. Magnetic resonance in medicine, 75(1), 441-451.

11. Eichner, C., Cauley, S. F., Cohen-Adad, J., Möller, H. E., Turner, R., Setsompop, K., & Wald, L. L. (2015). Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. NeuroImage, 122, 373-384.

12. Ades-Aron, B., Veraart, J., Kochunov, P., McGuire, S., Sherman, P., Kellner, E., ... & Fieremans, E. (2018). Evaluation of the accuracy and precision of the diffusion parameter EStImation with Gibbs and NoisE removal pipeline. NeuroImage, 183, 532-543.

13. Veraart, J., Fieremans, E., & Novikov, D. S. (2016). Diffusion MRI noise mapping using random matrix theory. Magnetic resonance in medicine, 76(5), 1582-1593.

14. http://neuromorpho.org

15. Lemberskiy, G., Baete, S., Veraart, J., Shepherd, T. M., Fieremans, E., & Novikov. D. S. (2019) Achieving sub-mm clinical di"usion MRI resolution by removing noise during reconstruction using random matrix theory. Proc 27th Annual meeting ISMRM, Montreal; 2019 (abstract 0770).

Figures

Fig. 1. a. By applying strong gradients G (Larmor gradient g=γG), magnetization far from the boundaries (cell membranes) vanishes, and that near the boundaries within a thickness of localization length l_g contributes to measured signal. This so-called localization regime emerges when l_g << diffusion length and cell dimension. b. Numerical simulation of diffusion inside an impermeable sphere (D₀=3 μm²/ms) demonstrates the localization regime at strong gradients (dashed line). The signal decay in localization regime is much slower than the free diffusion (dotted-dashed line).

Fig. 2. To increase the signal-to-noise ratio, the shot-to-shot phase variation in complex-valued DWIs is eliminated, and the subsequent real-valued DWIs are further processed and averaged over gradient directions for each b-shell. After averaging over real-valued images, the Rician noise floor is largely reduced. Here we show the DWIs of protocol 1 with t/δ = 27/16 ms as an example.

Fig. 3. dMRI measurements by using wide pulse sequence of strong gradients at 3 different diffusion times in 2 healthy subjects demonstrates the localization regime in the cortical brain gray matter, where diffusion signals coincide with the theory in Eq. (2) and yield a soma size estimation (Fig. 4). In contrast, diffusion signals in the brain white matter are not compatible to theory of localization regime since the axon size ~1 μm is smaller than the localization length l_g = 3.4-6.0 μm in experiments.

Fig. 4. The estimated soma radius r based on diffusion measurements of strong gradients in cortical gray matter (Fig. 3) and theory of localization regime in Eq. (2). The estimated radius r = 7 μm is longer than the localization length = 3.4-6.0 μm in experiments, a posteriori justifying the applicability of localization physics.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0639