Introduction

Respiratory motion during abdominal radiotherapy decreases the efficacy of treatments due to uncertainty in tumor location. The MR-LINAC^[1] was introduced as a combination of an MR-scanner and a radiotherapy LINAC, of which the ultimate potential is real-time 3D motion estimation (>5Hz^[2]) followed by the corresponding radiation beam adjustments. For these adjustments, it is crucial to quantify both motion and corresponding uncertainties; the radiation could be halted in case of high uncertainty, and resumed when confidence is restored. However, current state-of-the-art MRI-techniques cannot simultaneously perform real-time 3D motion-field estimation and uncertainty estimation.

Here, we present a probabilistic framework to perform simultaneous real-time 3D motion estimation and uncertainty quantification. We extend our preliminary work^[3] to a realistic prospective in-vivo setting, and demonstrate it on an MR-LINAC. The acquisition+processing time for 3D motion-fields is around 15ms, yielding a 67Hz frame-rate.

Theory

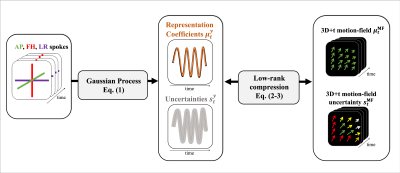
A Gaussian Process (GP) probabilistic model is combined with a low-rank motion representation basis. The representation basis relates low-dimensional representation coefficients to full 3D+t motion-fields, and the GP predicts a likelihood distribution of these representation coefficients from just three mutually orthogonal $$$k$$$-space readouts. Using the representation basis, these coefficients eventually yield the most likely 3D+t motion-fields and corresponding spatial uncertainties. See Fig. 1 for an overview of the framework.

Gaussian Process
We propose a predictive probabilistic model for the time-dependent motion-field representation coefficients $$$y^*$$$, as the conditional probability $$$\mathcal{P}(y^*|\mathbf{x}^*,\mathbf{X},\mathbf{Y})$$$, given on-line $$$k$$$-space measurements $$$\mathbf{x}^*$$$ and $$$N_t$$$ pairwise training samples $$$\mathbf{X}=[\mathbf{x}_1,\dots,\mathbf{x}_{N_t}],\mathbf{Y}=[y_1,\dots,y_{N_t}]^T$$$. The mean, $$$\mu_t^y$$$, denotes the most likely representation coefficient, and the variance, $$$s_t^y$$$, is a measure of uncertainty. For prediction purposes, the task is thus to estimate $$$\mu_t^y$$$ and $$$s_t^y$$$ from incoming data. We propose to implement the probabilistic predictive model as a Gaussian Process^[4] (GP), which provides closed-form, compact, analytical expressions for $$$\mu_t^y$$$ and $$$s_t^y$$$:\begin{array}{ccl}\mu^{y}_t&=&\mathbf{k}^T_t(\mathbf{K}+s^2\mathbf{I})^{-1}\mathbf{Y}\\s^{y}_t&=&k(\mathbf{x}_t^*,\mathbf{x}_t^*)+s^2-\mathbf{k}_t^T(\mathbf{K}+s^2\mathbf{I})^{-1}\mathbf{k}_t.\hspace{3cm}(1)\end{array}Here $$$\mathbf{K}$$$, $$$\mathbf{k}_t$$$ and $$$k(\mathbf{x}_t^*,\mathbf{x}_t^*)$$$ are quantities that depend on the covariance function and the training data. Intuitively, a GP learns how correlations in inputs ($$$k$$$-space) relate to outputs (motion-field coefficients). Prediction uncertainty increases when similarity between training and newly incoming data decreases, and could thus be used for quality assurance.

Low-rank motion-field compression
To obtain a motion-field compression basis, we extend MR-MOTUS^[5]. We perform a temporal-subspace-constrained motion-field reconstruction with rank-one low-rank MR-MOTUS, in which the temporal subspace is fixed to a 1D motion surrogate $$$\Psi$$$ derived from feet-head, anterior-posterior and left-right (FH,AP,LR) spokes^[6]:$$\boldsymbol{\Phi}=\textrm{arg}\min_{\boldsymbol{\Phi}}\hspace{0.5cm}\sum_{t} \lVert \mathbf{F}(\boldsymbol{\Phi}\Psi_t{|}\mathbf{q})-\mathbf{d}_t\rVert_2^2+\lambda\textrm{TV}(\boldsymbol{\Phi}{\Psi}_t).\hspace{2cm}(2)$$Here $$$\mathbf{F}$$$ denotes the MR-MOTUS model, $$$\boldsymbol{\Phi}$$$ the spatial compression basis, $$$\mathbf{q}$$$ a reference image, $$$\mathbf{d}_t$$$ $$$k$$$-space data at dynamic $$$t$$$, TV vectorial total-variation^[7], and $$$\lambda\ge{0}$$$ a regularization parameter. Note that (2) is different from low-rank MR-MOTUS, which also reconstructs for $$$\Psi$$$.

3D motion-field probability distribution
The GP is trained to predict time-dependent representation coefficients $$$\Psi_t$$$ and uncertainties $$$s^y_t$$$. However, for MR-guided radiotherapy, complete motion-fields and uncertainties are of interest. The coefficients and uncertainties can be projected back to a full 3D distribution of motion-fields (MF) through $$$\boldsymbol{\Phi}$$$:$$\begin{array}{ccl}{\mu}^\textrm{MF}_t&=&\boldsymbol{\Phi}{\mu}^{y}_t\\\mathbf{S}^\textrm{MF}_t&=&\boldsymbol{\Phi}s^{y}_t\boldsymbol{\Phi}^T,\hspace{3cm}(3)\end{array}.$$
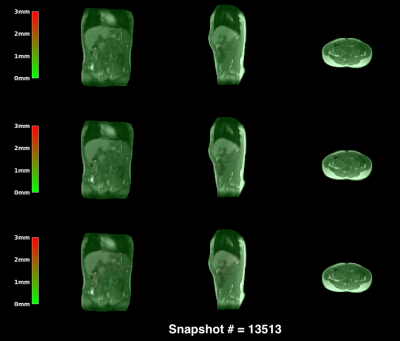
Here $$$\mathbf{S}^\textrm{MF}_t$$$ denote spatial covariance matrices that represent the uncertainty in the motion-fields (Fig. 4).

Methods

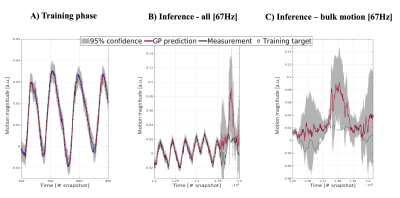
Data is acquired on an MR-LINAC from a healthy volunteer, who is instructed to perform 12 minutes of free-breathing, and 30 seconds bulk motion. The first 10 minutes, a 3D golden-mean radial acquisition is interleaved every 31 spokes with 3 spokes along all orthogonal axes (AP,LR,FH), and the last 2.5 minutes only the 3 orthogonal spokes were acquired (TR/TE/FA=4.8/1.8/20). A 1D motion surrogate was extracted from each set of AP,LR,FH spokes using PCA^[6]. The GP was trained to predict this surrogate for the first 10 minutes of data, given the three spokes as input. Besides the surrogate, the GP also provides uncertainty estimates (Eq. (3)), which are important for real-time quality assurance. The spatial compression basis was reconstructed from the same data, and the 1D motion surrogate was fixed as the temporal subspace. GP-inference was performed on the last 2.5 minutes of data, using only the three spokes as inputs that are acquired in 14.4ms. Finally, the GP predictions $$$\mu^y_t,s_t^t$$$ (Eq. (2)) are used to generate the full 3D motion-field distributions through Eq. (3).

Results

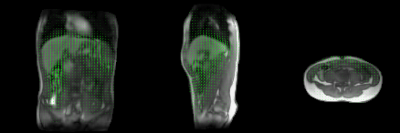
Fig. 2 shows the result of the GP training and inference.

Fig. 3 shows the motion-fields reconstructed with MR-MOTUS.

Fig. 4 shows the uncertainty in the motion-fields right before and during bulk motion.

Good correspondence with the motion surrogate can be observed. The uncertainty predictions clearly indicate bulk motion since incoming $$$k$$$-space data is very different from the training data. Processing times are in the order of milliseconds, yielding a total latency of around 15ms and a frame-rate of 67Hz for motion estimation and uncertainty predictions.

Discussion & Conclusion

We extended and experimentally validated a previously proposed probabilistic framework on an MR-LINAC. The framework allows for extremely fast data acquisitions, and joint non-rigid 3D motion estimation and uncertainty quantification on an MR-LINAC. All three aspects are crucial for MR-guided radiotherapy, but could previously not be addressed with state-of-the-art techniques, while the proposed framework addresses all of them simultaneously. Bulk motion is clearly present in the uncertainty predictions, and could thus be used for real-time quality assurance during MR-guided radiotherapy; the therapy can be halted in case of high uncertainty, and resumed if confidence is restored.

Acknowledgements

This research is funded by the Netherlands Organisation for Scientific Research (NWO), domain Applied and Engineering Sciences, Grant number 15115.