0624
MaxGIRF: Image Reconstruction Incorporating Maxwell Fields and Gradient Impulse Response Function Distortion1Biomedical Engineering, University of Southern California, Los Angeles, CA, United States, 2Cardiovascular Branch, Division of Intramural Research, National Heart, Lung, and Blood Institute, National Institutes of Health, Bethesda, MD, United States, 3Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, CA, United States
Synopsis
Non-Cartesian imaging can suffer from local blurring caused by concomitant fields and off-resonance. Concomitant fields are especially problematic when using prolonged non-Cartesian readouts with high gradient amplitudes at lower field strengths. We present a new reconstruction method, denoted MaxGIRF, for non-Cartesian imaging that corrects concomitant fields and trajectory errors without specialized hardware. The proposed method utilizes gradient impulse response functions to predict gradients waveforms which are in-turn used to estimate concomitant fields with analytic expressions. Image artifacts were successfully mitigated by the proposed method from 2D SE spiral imaging of the human brain acquired on a prototype 0.55T MRI system.
Introduction
Spiral imaging is complicated by the accrual of undesired spatially varying phase caused by the concomitant field, and static off-resonance1. The concomitant field, also known as Maxwell field, is generated whenever gradients are active2. Maxwell fields scale inversely with field strength. An elegant general correction approach was proposed by Wilm et al. that incorporates higher-order dynamic fields to the encoding process3. However, this method requires measurements from a dynamic field camera4-7 that adds cost and complexity, limiting its widespread use. Here, we propose a novel image reconstruction method, denoted MaxGIRF, that incorporates higher-order Maxwell fields and gradient impulse response function (GIRF) trajectory corrections, without requiring additional hardware. The proposed method relies on GIRFs measured with phantom-based methods and a good analytic model of concomitant fields that depends on coil geometry2,8 and gradient non-linearity9. We apply this method to a high-performance 0.55T MRI system, where SNR-efficient spiral acquisitions are attractive16.Theory
We consider the case where the net phase of all isochromats within a voxel is zero prior to the next RF pulse, such as spoiled gradient-echo and spin-echo sequences. Figure1 illustrates the steps to calculate a higher-order encoding matrix for MaxGIRF reconstruction. The GIRF is used to predict the actual gradient waveforms played on during the sequence. These predicted gradient waveforms are used to estimate the concomitant fields to generate the higher-order encoding matrices. Our current implementation uses explicit matrix-vector multiplications and does not apply any assumptions (e.g., low-rank approximation on higher-order encoding terms13)). The Tikhonov regularized least-squares problem is solved with a conjugate gradient algorithm3 written in BLAS21-23. Higher-order encoding matrices are precomputed for phantom studies and calculated on demand for in-vivo studies.Methods
Numerical simulationAn 8-interleaf, uniform-density spiral acquisition (26 msec readout) was simulated from an axial image of a MIDA brain phantom using 8 simulated receiver coils without noise14. System imperfections such as static off-resonance and eddy currents were not simulated. The B0 dependence (0.55/1.5/3/7T) and off-isocenter dependence (z=0,50,100,150,200 mm) of concomitant fields were simulated. The normalized mean squared error (NRMSE) between a Cartesian reference and spiral reconstructions were calculated.
Experimental Methods
Imaging experiments were performed on a high-performance 0.55T scanner (prototype MAGNETOM Aera, Siemens Healthcare, Erlangen, Germany)16,17. A 16-channel head/neck receive coil was used for phantom and in-vivo experiments. The Brodsky method was used to estimate first-order self-term GIRFs18,19 that were used to predict distorted gradients20.
Phantom experiments
Spiral axial scans of a NIST/ISMRM system phantom were acquired with a 2D GRE pulse sequence. A target slice was imaged at isocenter and 75 mm from isocenter, with parameters: FA=20°, TR/TE=100/1 ms, 8-interleaves, 11.8-ms, resolution=1.4x1.4 mm2, and FOV=22.4 cm. Ten repetitions were performed to reach steady-state.
Human experiments
In-vivo human brain scans (axial and sagittal) were acquired with a 2D interleaved multi-slice spiral spin-echo pulse sequence. Imaging parameters: FA=90°, TR/TE=745/15 ms, averages=10, 24-interleaves, 11.9-ms readout, resolution=0.75x0.75 mm2, and FOV = 24 cm.
Results
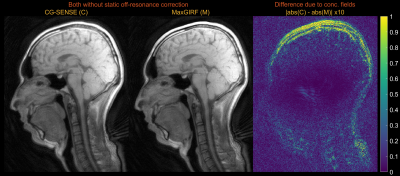
Figure 2 demonstrates noiseless numerical simulations of MaxGIRF reconstruction. The NRMSE (5.65%) for MaxGIRF at z = 0 mm with B0 = 0.55T shows the minimum achievable error, which is solely due to the difference between Cartesian and spiral image reconstructions since the concomitant field becomes zero at isocenter for axial orientation. Application of MaxGIRF reconstruction off-isocenter achieved this minimum error, indicating perfect correction of the concomitant fields.MaxGIRF reconstruction on axial spiral scans of a NIST/ISMRM phantom at 0.55T (Figure 3) and a human volunteer at 0.55T (Figures 4 and 5) show excellent performance. The blurring caused by the static off-resonance and concomitant fields is successfully removed as compared to conventional CG-SENSE reconstruction. The improvement in concomitant field blurring is evident in away from isocenter, as expected. The proposed reconstruction required 2 hours per slice (15 CG iterations x 450 sec per iteration) using a quad-core, 20 GB RAM laptop.
Discussion
MaxGIRF improves the sharpness of spiral acquisitions. Here we demonstrate the method using axial slices acquired at off-isocenter and peripheral regions of sagittal slices and will be applicable for low and high-field imaging.MaxGIRF estimates higher-order fields without NMR field probes but with theoretically derived analytic expressions of concomitant fields, which depend on coil geometry and gradient non-linearity. We presumed zero gradient non-linearity but noticed image distortions; gradient non-linearity could be incorporated with the MaxGIRF framework or post-hoc vendor corrections can be separately applied.
This work has several limitations. One is the large memory footprint (~80 GB) when precomputation of encoding matrices is used to speed-up explicit matrix-vector multiplications. This may be particularly challenging for 3D and/or very high-resolution spiral scans.
We did not consider acquisitions where the accrued net phase affects the spin phase after excitation or refocusing pulses in the following TR. This specifically includes bSSFP and FSE sequences, and remains future work.
Conclusion
MaxGIRF reconstruction is capable of removing spatial blurring caused by concomitant fields and static off-resonance. Non-Cartesian imaging with long readouts can benefit from this method. The impact could be greatest for high-performance low-field systems because the strength of concomitant fields scales with the maximum gradient amplitude and inversely to the main magnetic field. Compared to existing solutions, MaxGIRF is computationally intense, but does not require NMR field probes.Acknowledgements
†A.C.W. and K.S.N. should be considered joint senior author.
This work was supported by NSF #1828763, NIH R01-HL130494, and the NHLBI DIR (Z01-HL006039, Z01-HL005062). We would like to acknowledge the assistance of Siemens Healthcare in the modification of the MRI system for operation at 0.55T under an existing cooperative research agreement between NHLBI and Siemens Healthcare.
References
1. King KF, Ganin A, Zhou XJ, Bernstein MA. Concomitant gradient field effects in spiral scans. Magn. Reson. Med. 1999;41:103–112 doi: 10.1002/(SICI)1522-2594(199901)41:1<103::AID-MRM15>3.0.CO;2-M.
2. Bernstein MA, Zhou XJ, Polzin JA, et al. Concomitant gradient terms in phase contrast MR: Analysis and correction. Magn. Reson. Med. 1998;39:300–308 doi: 10.1002/mrm.1910390218.
3. Wilm BJ, Barmet C, Pavan M, Pruessmann KP. Higher order reconstruction for MRI in the presence of spatiotemporal field perturbations. Magn. Reson. Med. 2011;65:1690–1701 doi: 10.1002/mrm.22767.
4. De Zanche N, Barmet C, Nordmeyer-Massner JA, Pruessmann KP. NMR Probes for measuring magnetic fields and field dynamics in MR systems. Magn. Reson. Med. 2008;60:176–186 doi: 10.1002/mrm.21624.
5. Barmet C, De Zanche N, Pruessmann KP. Spatiotemporal magnetic field monitoring for MR. Magn. Reson. Med. 2008;60:187–97 doi: 10.1002/mrm.21603.
6. Barmet C, De Zanche N, Wilm BJ, Pruessmann KP. A transmit/receive system for magnetic field monitoring of in vivo MRI. Magn. Reson. Med. 2009 doi: 10.1002/mrm.21996.
7. Dietrich BE, Brunner DO, Wilm BJ, et al. A field camera for MR sequence monitoring and system analysis. Magn. Reson. Med. 2016;75:1831–1840 doi: 10.1002/mrm.25770.
8. Meier C, Zwanger M, Feiweier T, Porter D. Concomitant field terms for asymmetric gradient coils: Consequences for diffusion, flow, and echo-planar imaging. Magn. Reson. Med. 2008 doi: 10.1002/mrm.21615.
9. Wilm BJ, Hennel F, Roesler MB, Weiger M, Pruessmann KP. Minimizing the echo time in diffusion imaging using spiral readouts and a head gradient system. Magn. Reson. Med. 2020 doi: 10.1002/mrm.28346.
10. Scheffler K. A pictorial description of steady-states in rapid magnetic resonance imaging. Concepts Magn. Reson. 1999;11:291–304 doi: 10.1002/(SICI)1099-0534(1999)11:5<291::AID-CMR2>3.0.CO;2-J.
11. Markl M, Leupold J. Gradient Echo Imaging. 2012;1289:1274–1289 doi: 10.1002/jmri.23638.
12. Hargreaves BA. Rapid Gradient-Echo Imaging. 2012;1313:1300–1313 doi: 10.1002/jmri.23742.
13. Wilm BJ, Barmet C, Pruessmann KP. Fast higher-order MR image reconstruction using singular-vector separation. IEEE Trans. Med. Imaging 2012 doi: 10.1109/TMI.2012.2190991.
14. Iacono MI, Neufeld E, Akinnagbe E, et al. MIDA: A multimodal imaging-based detailed anatomical model of the human head and neck. PLoS One 2015 doi: 10.1371/journal.pone.0124126.
15. http://mrsrl.stanford.edu/~brian/vdspiral/
16. Campbell-Washburn AE, Ramasawmy R, Restivo MC, et al. Opportunities in interventional and diagnostic imaging by using high-performance low-field-strength MRI. Radiology 2019 doi: 10.1148/radiol.2019190452.
17. Restivo MC, Ramasawmy R, Bandettini WP, Herzka DA, Campbell-Washburn AE. Efficient spiral in-out and EPI balanced steady-state free precession cine imaging using a high-performance 0.55T MRI. Magn. Reson. Med. 2020 doi: 10.1002/mrm.28278.
18. Brodsky EK, Klaers JL, Samsonov AA, Kijowski R, Block WF. Rapid measurement and correction of phase errors from B0 eddy currents: Impact on image quality for non-cartesian imaging. Magn. Reson. Med. 2013;69:509–515 doi: 10.1002/mrm.24264.
19. Vannesjo SJ, Haeberlin M, Kasper L, et al. Gradient system characterization by impulse response measurements with a dynamic field camera. Magn. Reson. Med. 2013;69:583–93 doi: 10.1002/mrm.24263.
20. Campbell-Washburn AE, Xue H, Lederman RJ, Faranesh AZ, Hansen MS. Real-time distortion correction of spiral and echo planar images using the gradient system impulse response function. Magn. Reson. Med. 2016;75:2278–2285 doi: 10.1002/mrm.25788.
21. Scheffler K, Lehnhardt S. Principles and applications of balanced SSFP techniques. Eur. Radiol. 2003 doi: 10.1007/s00330-003-1957-x.
22. Bieri O, Scheffler K. Fundamentals of balanced steady state free precession MRI. J. Magn. Reson. Imaging 2013 doi: 10.1002/jmri.24163.
23. Jung BA, Weigel M. Spin echo magnetic resonance imaging. J. Magn. Reson. Imaging 2013 doi: 10.1002/jmri.24068.
24. Mugler JP. Optimized three-dimensional fast-spin-echo MRI. J. Magn. Reson. Imaging 2014 doi: 10.1002/jmri.24542.
Figures

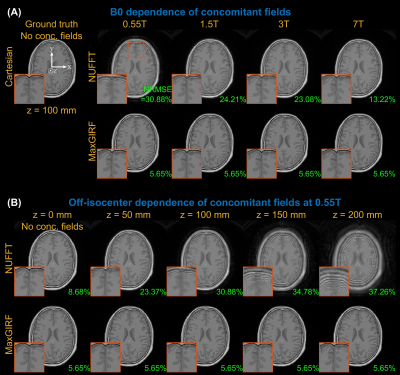
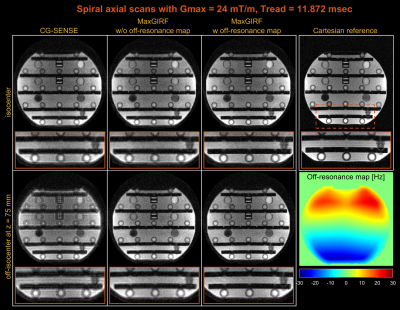
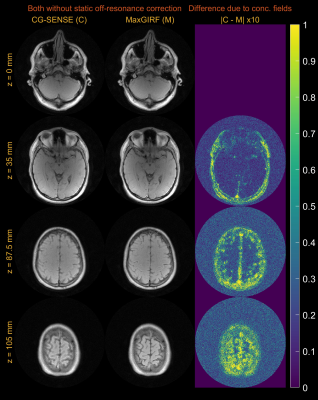
Figure 4. Multi-slice axial spiral imaging of a healthy volunteer at 0.55T. (left) CG-SENSE reconstructions; (middle) MaxGIRF reconstructions without static off-resonance correction (i.e., without a field map); (right) Absolute difference images. GIRF-predicted gradients were used in bothreconstructions. The improvement in concomitant field blurring is evident in away from isocenter, as expected. Static off-resonance correction was not performed, in order to isolate the difference due to concomitant field correction.