Introduction

Transmit radiofrequency (RF) field ($$$B_1^+$$$) inhomogeneity is a challenge at 7T, especially for specific absorption rate (SAR) demanding sequences such as 2D fast spin echo¹ (FSE). Previously, this has been tackled using parallel transmission and adjusting complex weights on each channel² (static RF shimming, [RFShim]), or by using combinations of RF and gradients to target a specific flip angle (FA) (SPINS³, k_T‑points^4,5, spokes⁶). Alternatively, direct signal control^7,8 (DSC), which has previously been experimentally applied to 2D⁹ and 3D⁷ FSE, leverages the degrees of freedom offered by the multiple refocusing pulses in FSE to dynamically adjust RF shimming and target homogeneous signal – with no impact on pulse shapes or sequence timing. In this work we show first results of an optimised and fully integrated implementation of DSC to 2D FSE brain imaging, under SAR control.

Methods

Environment

All experiments were performed on a MAGNETOM Terra (Siemens Healthcare, Erlangen, Germany) 7T scanner in research configuration, with an 8-Tx-channel head coil (Nova Medical, Wilmington MA, USA). Human subject scanning was approved by the Institutional Research Ethics Committee (HR-18/19-8700).
The scanner allowed for fully integrated field mapping and pulse design, happening in the background as part of the pre-acquisition adjustment steps. A FA map for each transmit channel was automatically acquired at a 4.0x4.0x10.0 mm³ resolution using saturation-prepared turbo FLASH¹⁰ (satprepTFL). Then, the scanner’s built-in pulse design environment was launched in the background during sequence adjustments.
Imaging was performed under first level SAR supervision on five healthy volunteers with the following T2w 2D FSE protocol: TE/TR = 79/5500 ms; echo spacing: 9.88 ms; echo train length: 11; 576x365 matrix, 0.36x0.48 mm² in-plane resolution; 34 transversal slices, 3 mm thickness; GRAPPA 3.

DSC Description and Comparison

DSC was assessed against RFShim in a 2D FSE imaging experiment. For RFShim, excitation used a 90° pulse and refocusing was performed under CPMG conditions^11,12 at 135° (157.5° for the first refocusing). A set of RF complex weights was determined and applied to all pulses using the vendor’s $$$B_1^+$$$ shimming technique, which solves a magnitude least-squares problem to minimise the spread of FA values in the field of view, within 130% of circular polarisation (CP) mode SAR.
DSC used an RFShim as starting point for the optimisation, then further tuned complex RF weights of each pulse independently to minimise signal differences from a target signal evolution⁹, solving:
$$
\DeclareMathOperator*{\argmin}{arg\,min}\qquad\qquad\argmin_{W}\sum_t\sum_v\sum_e{c_e\left\Vert\frac{s_{t,v,e}(W)-\hat{s}_{t,v,e}}{\Vert\hat{s}_{t,v,e}\Vert_1}\right\Vert}_2^2\qquad\qquad(1)\\[2em]\qquad\qquad\textrm{s.t. hardware and physiological constraints}
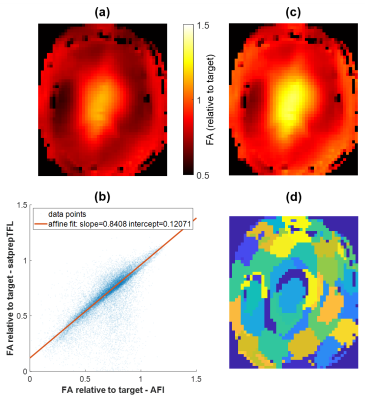
$$with $$$t$$$, $$$v$$$ and $$$e$$$ indexing respectively tissues considered, spatial locations and echo numbers in the refocusing train; $$$\hat{s}_{t,v,e}$$$ the target signal, $$$s_{t,v,e}$$$ the simulated signal depending on $$$W$$$ the matrix of complex weights applied to different pulses and channels; $$$c_e$$$ a weighting coefficient adjusting the contribution of each echo to the optimisation problem – here $$$c_e=0$$$ for early echoes, and $$$c_e$$$ linearly increases towards $$$e=8$$$ (k-space centre). $$$s_{t,v,e}$$$ and $$$\hat{s}_{t,v,e}$$$ were computed using the extended phase graph representation⁸. To preserve contrast two tissues were considered: grey matter (T1/T2 = 2000/100 ms) and cerebrospinal fluid (T1/T2 = 4400/2000 ms). To accelerate the calculation time 150 voxels were picked for signal optimisation via k‑means clustering as shown in Figure 1(d). Analytical derivatives of the cost-function and constraints were used. With a 50-iterations cap, optimisation times were about 1 min.

$$$B_1^+$$$ Map Correction

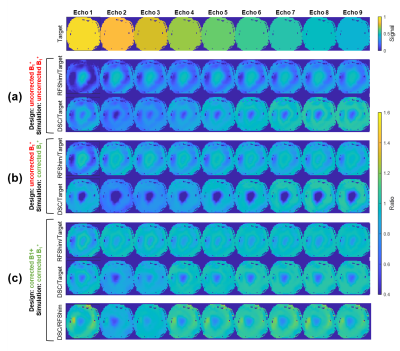
Since DSC relies on signal calculations, with errors propagating along the echo train, a prior investigation studied systematic errors in satprepTFL related to its transient readout. The actual FA imaging (AFI) sequence^13,14 was found more accurate but lengthier; it helped determine an experimental correction applied to satprepTFL. Figure 1 shows a scatter plot exhibiting affine relationship between the AFI and satprepTFL in a healthy volunteer. The following empirical correction was applied to relative CP mode $$$B_1^+$$$ maps ($$$\dot{\alpha}_{\mathrm{measured}}$$$):
$$
\qquad\qquad\qquad\dot{\alpha}_{\mathrm{corrected}}=1.18\,\dot{\alpha}_{\mathrm{measured}}-0.14\qquad\qquad\qquad(2)
$$
The corrected CP maps ($$$\dot{\alpha}_{\mathrm{corrected}}$$$) were then back-projected into per-channel maps. The quality and usefulness of the correction was assessed in simulation and in a DSC measurement.

Quality Assessment

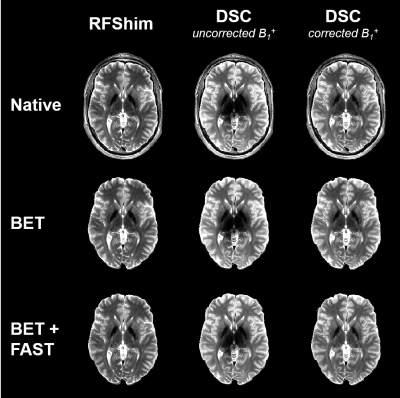
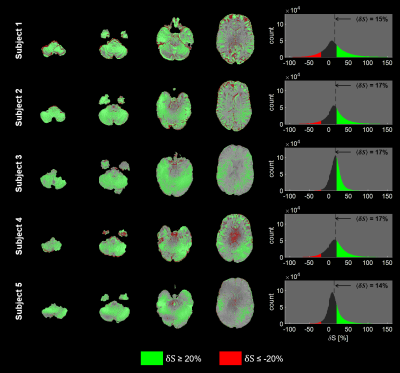
For result comparison, native images were brain-extracted with FSL^15–17 BET, then bias field correction was applied with FSL FAST to reduce the effect of reception profile (Figure 2). For a quantitative comparison between RFShim and DSC signals (respectively $$$S_\mathrm{RFShim}$$$ and $$$S_\mathrm{DSC}$$$), relative signal difference was calculated from brain-extracted images as:
$$
\qquad\qquad\qquad\qquad\delta{S}=\frac{S_\mathrm{DSC}-S_\mathrm{RFShim}}{S_\mathrm{RFShim}}\qquad\qquad\qquad\qquad(3)
$$Average values were reported for each subject.

Results

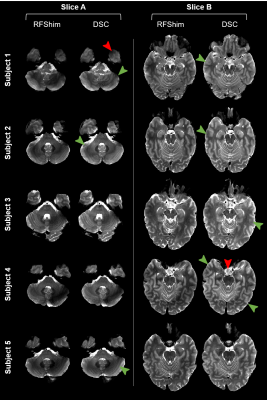
Figure 3 highlights the importance of $$$B_1^+$$$ correction, especially for DSC; this is visible in Figure 2 too. Figure 4 provides visual comparison of signal homogeneity and contrast in images acquired with RFShim and DSC. DSC shows superior homogeneity in lower brain areas, while preserving image quality in upper regions, under controlled SAR. This is also confirmed quantitatively in Figure 5, where DSC exhibits net signal gain over RFShim in all subjects, with average across subjects. Subject-averaged peak local SAR was 94% (SD: 6%) of limit for RFShim and 98% (SD: 3%) for DSC.

Conclusion

We have shown the effectiveness of DSC in providing better imaging quality than RFShim for 2D T2w TSE in routine conditions. Future developments will include better $$$B_1^+$$$ correction and measurement, tackle more weightings and investigate slice-by-slice optimisation.